Matplotlib - 3D Vignettes

---

---

A 3D vignette is a visual effect that focuses on a specific area of a three-dimensional object. It achieves this by gradually fading out or darkening the edges of the frame, helping to draw attention to the center of the image.

3D Vignettes in Matplotlib

A 3D vignette in Matplotlib refers to a visualization effect applied to three-dimensional objects to highlight specific parts of the object. It creates a sense of depth by changing the shade of color, generally darkening the edges compared to the center, to draw attention to particular regions.

Matplotlib does not have a specific function for directly applying a vignette effect to a plot. However, we can achieve the effect by adjusting the shading (color or transparency) manually.

Let’s start by drawing a spherical vignette.

Spherical Vignette

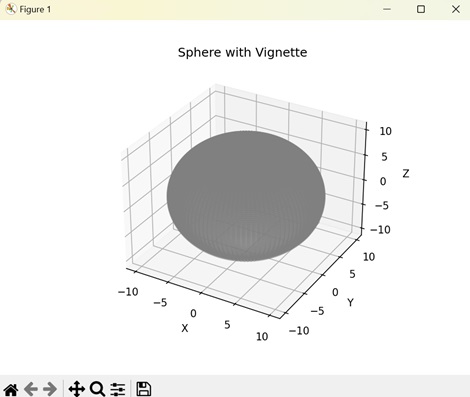
In Matplotlib, a spherical vignette represents a visual shading effect on the surface of a sphere. The shading is darker on the poles and lightens towards the center, creating a gentle transition of light and dark area.

Example

In the following example, we are creating a sphere with a vignette effect. We define the surface of the sphere using angles 'u' and 'v' and a "colormap" consisting of dark and light grey. The color at each point changes with the values of the Z coordinate. The resulting plot displays a sphere with varying shades of grey −

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import LinearSegmentedColormap

# Sphere with Vignette
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
x = 10 * np.outer(np.cos(u), np.sin(v))
y = 10 * np.outer(np.sin(u), np.sin(v))
z = 10 * np.outer(np.ones(np.size(u)), np.cos(v))

# Creating a sample 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

vignette_mask = np.exp(-(x**2 + y**2 + z**2))
cmap = LinearSegmentedColormap.from_list('vignette_color', [(0.5, 0.5, 0.5, 0), (0.5, 0.5, 0.5, 1)])
ax.scatter(x, y, z, c=z, cmap=cmap)

ax.set_title('Sphere with Vignette')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.show()

Output

Following is the output of the above code −

Toroidal Vignette

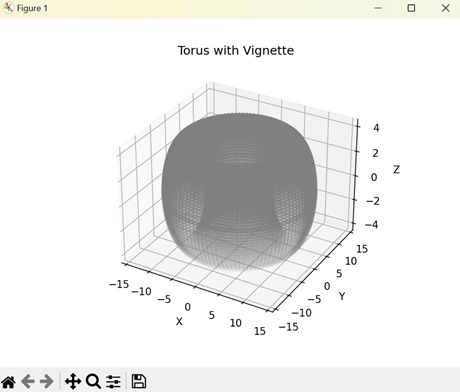
A toroidal vignette in Matplotlib creates a vignette effect on a torus (donut-shape) object. The outer edge which is further from the center is shaded dark while the inner edge which is closer to center is shaded light.

Example

In here, we are plotting a torus and applying vignette effect on it. We determine the torus size by major radius 'R' and minor radius 'r'. We then create a mask of grey color to apply shades at different areas of the torus −

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import LinearSegmentedColormap

# Torus with Vignette
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, 2 * np.pi, 100)
u, v = np.meshgrid(u, v)
R = 10
r = 4
x = (R + r * np.cos(v)) * np.cos(u)
y = (R + r * np.cos(v)) * np.sin(u)
z = r * np.sin(v)

# Creating a sample 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

vignette_mask = np.exp(-np.sqrt(x**2 + y**2 + z**2))
cmap = LinearSegmentedColormap.from_list('vignette_color', [(0.5, 0.5, 0.5, 0), (0.5, 0.5, 0.5, 1)])
ax.scatter(x, y, z, c=z, cmap=cmap)

ax.set_title('Torus with Vignette')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.show()

Output

Output of the above code is as follows −

Cylindrical Vignette

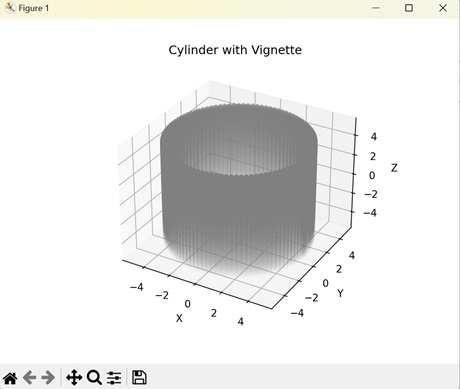
A cylindrical vignette in Matplotlib is a visual representation of vignette effect on a cylinder. The shade of the color is determined by the "Z" coordinate (depth) of the cylinder. As the depth decrease the vignette color shifts from dark to light.

Example

The following example applies a vignette effect on a cylinder. Here, we create a cylinder represented by parametric equations that vary with angle (theta) and height (h). Then, we shade the surface of the cylinder light or dark based on the exponential value of the height at different points −

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import LinearSegmentedColormap

# Cylinder with Vignette
theta = np.linspace(0, 2 * np.pi, 100)
h = np.linspace(-5, 5, 100)
theta, h = np.meshgrid(theta, h)
x = 5 * np.cos(theta)
y = 5 * np.sin(theta)
z = h

# Creating a sample 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

vignette_mask = np.exp(-np.abs(z))
cmap = LinearSegmentedColormap.from_list('vignette_color', [(0.5, 0.5, 0.5, 0), (0.5, 0.5, 0.5, 1)])
ax.scatter(x, y, z, c=z, cmap=cmap)

ax.set_title('Cylinder with Vignette')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.show()

Output

After executing the above code, we get the following output −

Helical Vignette

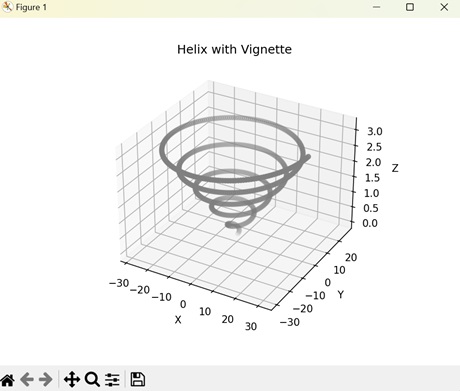
In Matplotlib, a helical vignette represents a shading effect on a coiled shape that stretches upwards. The vignette effect is darker towards the outer edges while lighter towards the points closer to the center.

Example

Now, we are applying a vignette effect on a helix. To create the helix, we parametrize the X, Y, and Z coordinates based on time (t). We then assign a "gray" colormap based on the depth of the helix. This creates a helical structure with different shades of dark and light based on the distance from center −

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import LinearSegmentedColormap

# Helix with Vignette
t = np.linspace(0, 10 * np.pi, 1000)
x = t * np.cos(t)
y = t * np.sin(t)
z = 0.1 * t

# Creating a sample 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

vignette_mask = np.exp(-np.abs(z))
cmap = LinearSegmentedColormap.from_list('vignette_color', [(0.5, 0.5, 0.5, 0), (0.5, 0.5, 0.5, 1)])
ax.scatter(x, y, z, c=z, cmap=cmap)

ax.set_title('Helix with Vignette')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.show()

Output

The output obtained is as shown below −