Abstract
Background
Next-generation sequencing technologies revolutionized genomics by producing high-throughput reads at low cost, and this progress has prompted the recent development of de novo assemblers. Multiple assembly methods based on de Bruijn graph have been shown to be efficient for Illumina reads. However, the sequencing errors generated by the sequencer complicate analysis of de novo assembly and influence the quality of downstream genomic researches.
Results
In this paper, we develop a de Bruijn assembler, called Clover (clustering-oriented de novo assembler), that utilizes a novel k-mer clustering approach from the overlap-layout-consensus concept to deal with the sequencing errors generated by the Illumina platform. We further evaluate Clover’s performance against several de Bruijn graph assemblers (ABySS, SOAPdenovo, SPAdes and Velvet), overlap-layout-consensus assemblers (Bambus2, CABOG and MSR-CA) and string graph assembler (SGA) on three datasets (Staphylococcus aureus, Rhodobacter sphaeroides and human chromosome 14). The results show that Clover achieves a superior assembly quality in terms of corrected N50 and E-size while remaining a significantly competitive in run time except SOAPdenovo. In addition, Clover was involved in the sequencing projects of bacterial genomes Acinetobacter baumannii TYTH-1 and Morganella morganii KT.
Conclusions
The marvel clustering-based approach of Clover that integrates the flexibility of the overlap-layout-consensus approach and the efficiency of the de Bruijn graph method has high potential on de novo assembly. Now, Clover is freely available as open source software from https://oz.nthu.edu.tw/~d9562563/src.html.
Keywords: De novo genome assembly, DNA sequencing, De bruijn graph
Background
Massively parallel DNA sequencing has become a prominent tool in biological research [1, 2]. The high-throughput and low cost of next-generation sequencing technologies produce high coverage of reads. The Illumina platform is one of the most commonly used sequencers, producing reads with lengths ranging from 35 to 300 bp. The de Bruijn graph approach is prevalent in the de novo assembly using Illumina reads, and it constitutes all possible substrings of length k (termed k-mers) from the reads to efficiently process the huge sequencing data. Choosing the length of k is an important issue in the de Bruijn graph approach. Theoretically, for reads without sequence errors, smaller k-mers increase the connectivity of the graph and larger k-mers decrease the number of ambiguous repeats in the graph. There is therefore a balance between sensitivity and specificity determined by k [3]. However, for reads with errors, larger k-mers decrease the sensitivity and specificity further due to sequencing errors generated by the Illumina platform, in which the primary errors are substitution errors, at rates of 0.5–2.5% [4].
In this study, we are trying to answer what happens if we design an approach to allow such errors on k-mers, and could the error allowance on k-mers improve the quality of de novo assembly. Therefore we developed a clustering-oriented approach, called Clover, to deal with those substitution errors, and use a new parameter p which describes the level of error allowance on k-mers. For example, setting k to 40 and p to 1 means that our algorithm uses each 40-mers in the input reads while allowing each of them to have the flexibility of 1 substitution error.
With the flexibility of error allowance on k-mers, Clover tries to cluster these k-mers together when their Hamming distance less than or equal to p, and merges each cluster of k-mers to a node by finding its consensus sequence. To avoid over-merging of clusters, which may occur on the boundary of repeat sequence, Clover will split each node into multiple nodes when the merged node has multiple major consensus sequences (see Implementation section for detail).
After the steps mentioned above, the number of nodes in the graph will dramatically reduce, which therefore simplifies analysis of assembly. For example, Table 1 compares three results of a Leptospira shermani assembly when using different level of error allowance (p = 0, 1 and 2). Setting p to 0 is equal to run our assembler with traditional de Bruijn-based approach, which does not have the flexibility of error allowance on k-mers. The assembly result shows that only setting p to 1 could dramatically increase the N50 both in contig and scaffold because it reduces the number of nodes to build the de Bruijn graph that increases the specificity. The result also shows that setting p to 2 only increases the N50 on contig whereas decreases on scaffold. In this case, reducing too many nodes could increase the specificity, but it seems losing some meaningful information, which decreases the sensitivity at the same time.
Table 1.
The clustering effect of Clover on Leptospira shermani assemblies
| p | Nodes | Contigs | Scaffolds | Time (min) | Memory (GB) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Num | Total (kb) | Max (kb) | N50 (kb) | Num | Total (kb) | Max (kb) | N50 (kb) | ||||
| 0 | 33,692,986 | 5070 | 3818 | 9 | 1.0 | 182 | 3947 | 178 | 54 | 45.8 | 17.7 |
| 1 | 15,969,082 | 1201 | 3875 | 34 | 5.5 | 117 | 3897 | 196 | 85 | 30.5 | 16.2 |
| 2 | 11,917,810 | 1103 | 3859 | 27 | 6.1 | 117 | 3880 | 145 | 63 | 36.0 | 11.7 |
p the level of error allowance on the k-mers, Nodes the number of nodes to build de Bruijn graph, Num the number of sequences produced, Total the total length of sequences produced, Max the maximum length of sequences produced, N50 the N50 statistic calculated with respect to the total length of sequences produced, Time the run time to assemble the genome, Memory the memory requirement to assemble the genome
The memory requirements, as shown in Table 1, are in clear proportion to the number of nodes to build the de Bruijn graph, but are not in obvious proportion to parameter p (Additional file 4: Table S1, compares the memory requirements when using different k and p). The time cost is dropped when setting p to 1 due to the benefit of simplifying analysis, but setting p to 2 could not get the benefit more. Together with the phenomena described above, we should choose a suitable p, not as large as possible. In the case of L. shermani assembly, the suitable p is 1 and p/k is 2.5%, which is nearly the error rate of Illumina platform.
Implementation
Clover proceeds through the following phases whose flowchart is shown in Fig. 1.
Fig. 1.
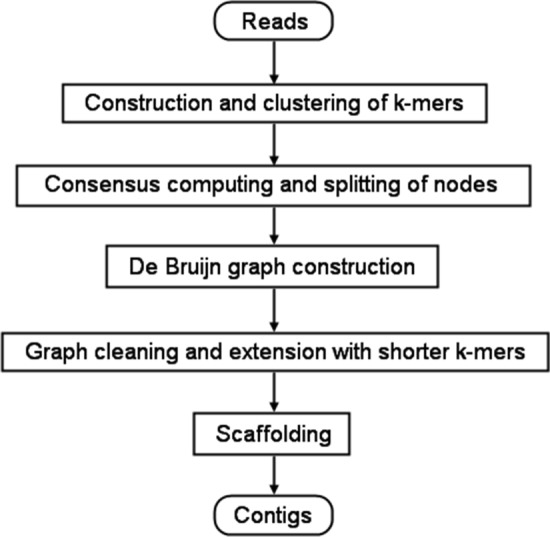
The flowchart of the Clover pipeline
Construction and clustering of k-mers
For given k (k-mer) and p (error allowance), Clover constructs a Hamming graph by extracting all the input k-mers as nodes. The graph’s edges are created by the pairs of k-mers if the Hamming distance of the k-mers (or their reverse complements) is ≤ p. Figure 2 illustrates an example of 5-mers clustering while allowing 1 error. Basically, the components of the Hamming graph are the clusters of k-mers (Fig. 2b). Clover then merges all the nodes within each component of the Hamming graph into a single node and computes its consensus sequence. In practice, just setting p to (k × error rate of sequencer) can dramatically reduce the number of k-mers for constructing the de Bruijn graph later and accelerates the subsequent graph processing. In the implementation, Clover uses two steps to cluster the k-mers: Step 1 extracts all k-mers from the input reads. Step 2 constructs a Hamming graph of the k-mers and then performs a breadth-first search to find each component in the Hamming graph. If there is no error allowance needed (p = 0), Clover will omit the process of step 2.
Fig. 2.
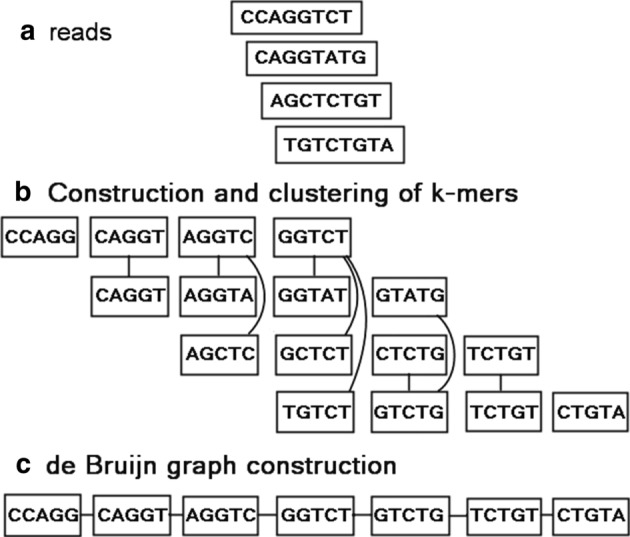
An example of 5-mers clustering while allowing 1 error
Consensus computing and splitting of nodes
Clover computes the consensus sequence for each merged node by selecting the nucleotide with the most occurrence on each base pair. For example, the fourth component of Fig. 2b has 4 k-mers (GGTCT, GGTAT, GCTCT and TGTCT) whose consensus sequence therefore is GGTCT as shown in Fig. 2c. To avoid over-merging, if the k-mers of the merged node, called v, have a nucleotide on a base pair, called x, whose occurrence is closed to that of the corresponding nucleotide, called y, in the consensus sequence, Clover splits the merged node into multiple nodes. More realistically, given a fractional threshold sp, if the occurrence of x is greater than or equal to sp times the occurrence of y, Clover collects all the k-mers with x into a new node, called v1, leaves the others into a new node, called v2, and recursively retries this splitting process on v1 and v2. Let q be the number of k-mers in the merged node. Then the consensus computing requires O(q × k) time, the condition checking requires O(k) time and collecting the k-mers into the new nodes requires O(q) time. Therefore, similar to the analysis of quick sort, the worst case of the time complexity on the whole process is O(q2 × k). Figure 2c shows the resulting consensus sequences of Fig. 2b by setting sp to 0.6. Finally, Clover collects all the resulting consensus sequences as the k-mer set for constructing de Bruijn graph in the next phase.
De Bruijn graph construction
For the k-mer set obtained in the previous phase, Clover constructs the de Bruijn graph by directly using the k-mer set as its node set. For any two nodes, it creates an edge between them if their corresponding k-mers have an overlapping of length k − 1. Figure 2c provides an example for de Bruijn graph construction.
Graph cleaning and extension with shorter k-mers
Clover provides multiple operations based on spectrum, structure and their combination for removing spurious edges from the de Bruijn graph. The spectral error removal operation is the trimming of low-frequency edges. The structural error removal operations are the pruning of tips, bubbles, and erroneous connections. If there are multiple options during pruning of tips and bubbles, Clover prunes the low-frequency edges first. All these operations were also used in SOAPdenovo [5] and Velvet [3]. Clover then iteratively extends the graph by connecting two paths if the sequences of the paths have an overlapping length shorter than k until the given minimum overlapping length m is achieved. Clover defaultly sets the parameter m to (k/2) + 1. For example, we compare the different settings of m on the Rhodobacter sphaeroides assemblies (see Additional file 4: Table S2), where k is set to 46 in this case, and find that the default value 24 of m has the best scaffold result.
Scaffolding
Clover utilizes read-pair information by aligning both ends of the pairs to the paths in the graph to find pairs of anchors. Given a scaffold support ss, which defaultly is set to 5, Clover links each pair of paths with the consistent bound if its support from the pairs of anchors is greater than or equal to ss. Clover calculates the medium length of insert sizes inferred from the pairs of anchors to be the consistent bound of the linked pair of paths. Finally, Clover predicts contigs by searching Eulerian super-paths on the graph.
Results and discussion
To evaluate the assembly correctness of Clover, we have tested three typical datasets in the GAGE study: Staphylococcus aureus (2.9 Mb), Rhodobacter sphaeroides (4.6 Mb) and human chromosome 14 (88.3 Mb) [6]. Each dataset has original reads, Quake corrected reads and Allpaths-LG corrected reads. The result with the best scaffold N50 on these three datasets is selected for assembly comparison we will discuss later.
Running Clover assembler
We provide Clover source code with this submission (see Additional file 1) and at our website https://oz.nthu.edu.tw/~d9562563/src.html.
Installation of Clover is provided at Additional file 2.
Each dataset in the GAGE study (see Additional file 2) is available at https://gage.cbcb.umd.edu/data/.
For testing Clover, test data is available at ‘Test Case’ of our website.
In Table 2, the results of our Clover were obtained from Allpaths-LG corrected reads. The assembly instructions used by our Clover are:
S. aureus: clover -k 32 -p 0 -i1 frag_1.fastq,shortjump_1.fastq -i2 frag_2.fastq,shortjump_2.fastq -cs 5 -ss 3 -is 180,3500 -hp 0.6 -pm -ml 700.
R. sphaeroides: clover -k 46 -p 0 -i1 frag_1.fastq,shortjump_1.fastq -i2 frag_2.fastq,shortjump_2.fastq -cs 7 -ss 3 -is 180,3500 -hp 0.6 -pm -ml 200.
Human chromosome 14: clover -k 80 -p 3 -i1 frag_1.fastq,shortjump_1.fastq,longjump_1.fastq -i2 frag_2.fastq,shortjump_2.fastq,longjump_2.fastq -cs 9 -ss 5 -is 155,2543,35306 -hp 0.8 -ml 900.
Table 2.
Comparison of assemblers on Staphylococcus aureus (SA), Rhodobacter sphaeroides (RS) and human chromosome 14 (HG)
| Data (Mb | Assembler | Contigs | Scaffolds | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Num | N50 (kb) | E-size (kb) | Errs | N50C (kb) | E-sizeC (kb) | Num | N50 (kb) | E-size (kb) | Errs | N50C (kb) | E-sizeC (kb) | ||
| SA | Clover | 128 | 43.9 | 53.1 | 13 | 41.3 | 50.5 | 12 | 1490 | 947 | 2 | 1490 | 890 |
| 2.9 | ABySS | 90 | 129.1 | 181.1 | 16 | 69.8 | 102.5 | 61 | 170 | 199 | 0 | 107 | 127 |
| Bambus2 | 109 | 50.2 | 69.1 | 178 | 16.7 | 19.5 | 17 | 1084 | 1120 | 0 | 1084 | 1120 | |
| CABOG | Could not run because of incompatible read lengths in one library | ||||||||||||
| MSR-CA | 94 | 59.2 | 60.4 | 22 | 49.2 | 51.4 | 17 | 2412 | 2026 | 1 | 1022 | 1039 | |
| SGA | 1252 | 4.0 | 4.7 | 3 | 4.0 | 4.7 | 546 | 208 | 166 | 2 | 208 | 164 | |
| SOAPdenovo | 107 | 288.2 | 252.3 | 58 | 62.7 | 67.5 | 99 | 332 | 302 | 0 | 288 | 227 | |
| SPAdes | 98 | 62.6 | 87.9 | 9 | 57.0 | 75.1 | 41 | 1703 | 1144 | 2 | 684 | 570 | |
| Velvet | 162 | 48.4 | 60.3 | 19 | 41.5 | 49.8 | 45 | 762 | 664 | 18 | 284 | 282 | |
| RS | Clover | 453 | 20.1 | 23.8 | 19 | 19.5 | 21.9 | 59 | 2483 | 1795 | 1 | 2483 | 1795 |
| 4.6 | ABySS | 644 | 19.7 | 25.1 | 57 | 13.3 | 18.5 | 414 | 51 | 56 | 0 | 46 | 47 |
| Bambus2 | 177 | 93.2 | 94.5 | 360 | 12.8 | 16.3 | 92 | 2439 | 1375 | 1 | 390 | 1106 | |
| CABOG | 322 | 20.2 | 24.1 | 31 | 17.9 | 21.5 | 130 | 66 | 520 | 3 | 65 | 381 | |
| MSR-CA | 395 | 22.1 | 24.2 | 32 | 19.1 | 21.5 | 43 | 2976 | 2039 | 3 | 2976 | 2017 | |
| SGA | 3067 | 2.3 | 3.3 | 4 | 2.3 | 3.3 | 2096 | 51 | 53 | 0 | 51 | 53 | |
| SOAPdenovo | 204 | 131.7 | 157.2 | 401 | 14.6 | 18.7 | 166 | 660 | 688 | 0 | 660 | 559 | |
| SPAdes | 768 | 11.8 | 13.7 | 7 | 11.7 | 13.5 | 352 | 718 | 840 | 0 | 718 | 840 | |
| Velvet | 583 | 15.7 | 18.6 | 24 | 14.5 | 16.9 | 178 | 353 | 380 | 16 | 301 | 352 | |
| HG | Clover | 24,527 | 3.4 | 5.3 | 718 | 3.2 | 5.0 | 2089 | 839 | 943 | 385 | 409 | 502 |
| 88.3 | ABySS | 21,222 | 14.7 | 19.0 | 1876 | 10.4 | 13.4 | 19,249 | 18 | 24 | 13 | 13 | 19 |
| Bambus2 | 13,592 | 5.9 | 23.3 | 8175 | 4.3 | 6.3 | 1792 | 324 | 528 | 240 | 200 | 274 | |
| CABOG | 3361 | 45.3 | 58.8 | 2346 | 23.7 | 30.6 | 479 | 393 | 549 | 39 | 309 | 457 | |
| MSR-CA | 30,103 | 4.9 | 6.8 | 1656 | 4.3 | 5.9 | 1425 | 893 | 1420 | 1430 | 282 | 407 | |
| SGA | 56,939 | 2.7 | 3.8 | 375 | 2.7 | 3.7 | 30,975 | 83 | 113 | 24 | 81 | 111 | |
| SOAPdenovo | 21,818 | 16.7 | 21.9 | 6587 | 7.8 | 10.4 | 13,502 | 454 | 533 | 384 | 227 | 276 | |
| SPAdes | 16,854 | 12.7 | 16.7 | 1519 | 10.4 | 13.6 | 9245 | 173 | 223 | 199 | 129 | 162 | |
| Velvet | 45,564 | 2.3 | 3.3 | 3665 | 2.1 | 3.0 | 3565 | 1190 | 1825 | 8659 | 86 | 124 | |
Num the number of sequences produced, N50 the N50 statistic calculated with respect to the genome size, E-size the most likely size of the sequence containing some random base in the genome, Errs the number of misjoins and for the contig value, also the number of indels > 5 bases, N50C the N50 calculated after splitting all sequences at error locations, and E-sizeC the E-size calculated after splitting all sequences at error locations. The best result in each column, for each dataset, is indicated in bold
The assembly results display all statistics data in the screen (see Additional file 3: Section S2) and create two assembly output files named out_contig.fasta and out_scaffold.fasta.
Running Leptospira shermani assembly
We provide Leptospira shermani dataset tar file at our website https://oz.nthu.edu.tw/~d9562563/src.html.
Download and unpack it: tar -zxvf leptospirashermanidata.tar.gz.
The assembly instructions are: clover -k 40 -p ? -is 485 -i1 Lepto_500_1.fq -i2 Lepto_500_2.fq -hp 0.6, where ? runs with 0, 1 and 2, respectively.
The assembly results display all statistics data in the screen (see Additional file 3: Section S1) and create two assembly output files named out_contig.fasta and out_scaffold.fasta.
Assemblers
Table 2 shows the comparison of Clover’s performance against several modern assemblers, which include ABySS [7], Bambus2 [8], CABOG [9], MSR-CA [10], SGA [11], SOAPdenovo [5], SPAdes [12] and Velvet [3]. All assembly statistics were generated by the GAGE validation scripts. Bambus2, CABOG and MSR-CA are well known overlap-layout-consensus assemblers, while ABySS, SOAPdenovo, SPAdes and Velvet are famous de Bruijn graph assemblers and SGA is typical string graph assembler.
Comparison
For the S. aureus dataset, SOAPdenovo and ABySS have produced the longest two contigs. SGA, SPAdes, Clover and ABySS have been detected the fewest four errors in contigs, but SOAPdenovo contains many errors. Therefore ABySS achieves the longest corrected contigs. MSR-CA has produced the longest scaffolds, but its longest scaffold has been broken by an error. Instead, Clover and Bambus2 achieve the longest corrected scaffolds in terms of N50 and E-size respectively.
For the R. sphaeroides dataset, SOAPdenovo and Bambus2 have produced the longest two contigs. However, considering the assembly correctness, Clover achieves the longest corrected contigs. SGA and SPAdes contain fewest two errors in contigs, but their N50 lengths are relatively shorter. Excluding SGA and SPAdes, Clover’s contigs contain fewest errors. On the other hand, MSR-CA and Clover have the best two scaffold results both in uncorrected and corrected N50.
For the human chromosome 14 dataset, Clover produces the relatively conservative contigs, but its contigs contain fewest errors except SGA. CABOG has the best contig results both in uncorrected and corrected N50. Velvet produces the longest scaffolds. However, when focusing on the assembly correctness, Clover achieves the longest corrected scaffolds.
Note that the N50 statistics is defined as the minimum contig length (in descending order) needed to cover 50% of the genome. The N50 statistics generated by Clover is the minimum contig length needed to cover 50% of all the sequence produced. However, the N50 statistics generated by the GAGE validation scripts is the minimum contig length needed to cover 50% of the reference genomic sequence provided in GAGE study. Therefore the N50 statistics of Clover in Additional file 3 and the N50 statistics of Clover in Table 2 have a little difference.
The result of L. shermani seems to be poorer than S. aureus and R. sphaeroides. However, these two datasets in GAGE study have two libraries and the fragment size is up to 3500 bp [6], whereas the L. shermani dataset only has single library with fragment size 485 bp. The better assembly quality is caused by using more libraries. Practically, researchers usually use optical mapping to arrange scaffolds and then obtain the draft sequence [12].
In addition, our clustering approach can apply on ever error-corrected reads. For example, the assembly of human chromosome 14 is generated by clustering 80-mers while allowing 3 errors on Allpaths-LG corrected reads. Therefore Clover would not conflict with current error correction tools. In practice, we will apply smaller k-mer on single library or lower coverage dataset such as the L. shermani assembly, and larger k-mer on more complex genomes such as human chromosome 14. When using large k-mer, increasing the level of error allowance is especially needed even on ever error-corrected reads.
Run times and memory requirements
To assess Clover’s run times and memory requirements, we have rerun above assemblers that follow the same processes and parameters of GAGE with their newest version on a 16-core AMD Opteron 6128 2 GHz server with 256 GB of RAM. The parameters of optimal result seem varying with the different version of assemblers and hence we only take their run times and memory requirements into comparisons. Because we don’t have large-scale parallel environment, we only run ABySS on single-process version.
Table 3 shows the comparison of these assemblers on run times and memory requirements. The result shows that the run time of Clover is significantly competitive to those efficient de Bruijn graph assemblers except SOAPdenovo. SOAPdenovo is the fastest assembler due to the multi-process parallelization.
Table 3.
Comparison of assemblers on run times and memory requirements
| Assembler | Staphylococcus aureus | Rhodobacter sphaeroides | Human Chromosome 14 | |||
|---|---|---|---|---|---|---|
| Time | Memory | Time | Memory | Time | Memory | |
| Clover | 5.6 min | 10.1 GB | 13.9 min | 11.0 GB | 10.4 h | 59.3 GB |
| ABySS | 5.1 min | 0.5 GB | 11.6 min | 0.5 GB | 6.7 h | 3.3 GB |
| Bambus2 | 55.5 min | 2.3 GB | 3.7 h | 12.3 GB | 5.1 d | 190.3 GB |
| CABOG | NA* | NA* | 2.9 h | 12.3 GB | 22.9 h | 190.4 GB |
| MSR-CA | 25.5 min | 26.2 GB | 41.3 min | 28.3 GB | 1.3 d | 34.6 GB |
| SGA | 35.5 min | 1.1 GB | 1.1 h | 3.5 GB | 18.8 h | 35.0 GB |
| SOAPdenovo | 2.3 min | 3.1 GB | 1.8 min | 5.0 GB | 2.1 h | 8.0 GB |
| SPAdes | 56.8 min | 6.1 GB | 29.5 min | 4.5 GB | 10.9 h | 22.0 GB |
| Velvet | 5.4 min | 0.4 GB | 7.3 min | 0.5 GB | 11.7 h | 72.3 GB |
Time the run time to assemble the genome, Memory the memory requirement to assemble the genome
*NA, could not run because of incompatible read lengths in one library
The major cost of Clover is the k-mers clustering. In the k-mers clustering, Clover constructs a Hamming graph in which it links each pair of k-mers as an edge if the Hamming distance of the pair of k-mers is ≤ p. To accelerate the process, Clover utilizes the indexing technique that partitions a k-mer into (p + 1) substrings. If the Hamming distance of a pair of k-mers is ≤ p, there must exist a pair of substrings that are exactly the same. Therefore Clover uses (p + 1) hash tables which index each substring of all k-mers to find the candidate pairs of k-mers, and performs comparisons to check their real Hamming distances. Let n be the number of the reads. l be the length of the reads, k be the length of k-mers and p be the level of error allowance on the k-mers. Note that p can be 0 in this study. Then n × (l − k + 1) is the number of k-mers within the reads, (p + 1) is the number of hash tables needed to find the candidate pairs of k-mers and each comparison for them requires O(k) time. Therefore, the worst case of the time complexity on k-mers clustering is O(n × (l − k + 1) × k × (p + 1)) ≅ O(n × (l − k) × k × (p + 1)). Similarly, the memory needed to store all the sequences of the k-mers is O(n × (l − k) × k), and the memory needed for all the k-mers on the hash tables is O(n × (l − k) × (p + 1)). Since k is much larger than p, the worst case of the space complexity on k-mers clustering is O(n × (l − k) × k).
Sequencing projects
It is worth mentioning that Clover was involved in two sequencing projects to respectively sequence bacterial genomes Acinetobacter baumannii TYTH-1 (4.0 Mb and 165 contigs) [14] and Morganella morganii KT (3.8 Mb and 58 contigs) [15]. The contigs generated by Clover were then used to build the draft sequences, which were confirmed by optical mapping and PCR. From the draft sequences of A. baumannii TYTH-1 and M. morganii KT, 3682 and 3565 protein-coding sequences, 75 and 72 tRNA genes, and 6 and 10 rRNA genes were further predicted, respectively. Table 4 shows the summary of these two sequencing results.
Table 4.
The results of two bacterial genome sequencing projects
| Acinetobacter baumannii TYTH-1 | Morganella morganii KT | |
|---|---|---|
| Length of sequence | 3,957,368 bp | 3,826,919 bp |
| Number of contigs | 165 | 58 |
| GC content | 39% | 51% |
| Number of protein-coding sequences | 3682 | 3565 |
| Number of tRNA genes | 75 | 72 |
| Number of rRNA genes | 6 | 10 |
| GenBank accession number | CP003856 | ALJX00000000 |
The NGS datasets of these two bacterial sequencing projects are available for download at https://oz.nthu.edu.tw/~d9562563/src.html
Limitations
The limit of our current Clover is that it cannot apply on genomes with large size up to 250 Mb. This is caused by 256 GB of RAM in our server (see Run times and memory requirements section for detail). However, if the server has more RAM, the limitation could be eliminated. The memory requirement issue exists in many assemblers with which we compared in this study. As shown in Table 3, if a genome can not be assembled by Clover, the genome has the high probability that it can not be assembled by other assemblers we used in this study.
Future works
We leave the parallelization of program as a future work that will further improve the performance of Clover. Besides, we leave the exploration of other possible clustering algorithms to further improve Clover as another future work.
Conclusions
In this study, we developed a new clustering-oriented de novo assembler, called Clover, that integrates the flexibility of the overlap-layout-consensus approach on clustering k-mers and the efficiency of the de Bruijn graph method, with which we improve the robustness with respect to sequencing error especially using large k-mers. We discovered the effect of our clustering approach that not only improves the assembly result but also accelerates the assembly process by simplifying analysis on the Leptospira shermani assembly. The evaluation of Clover on GAGE datasets finally shows that it achieves a superior assembly quality in terms of corrected N50 and E-size while remaining a significantly competitive in run time.
Availability and requirements
Project name Clover.
Project home page https://oz.nthu.edu.tw/~d9562563/
Operating system(s) Linux.
Programming language C, Python and Cython.
Other requirements Python-devel to develop Python extensions.
License GNU GPL2.
Any restrictions to use by non-academics None.
Supplementary information
Clover source code for Linux. Please refer to ‘Installation of Clover’.
Datasets and Installation of Clover. GAGE dataset list and locations, and build Clover’s executing and programming environments.
Section S1—Leptospira shermani assembly statistics results. Section S2—Clover assembly statistics results. Clover output screen text.
Table S1—Memory requirements (GB) of k versus p correlation on Leptospira shermani assembly. Table S2—Sensitivity comparison of different minimum overlapping lengths on Rhodobacter sphaeroides assembly. Supplemental analysis of Clover.
Acknowledgements
The authors appreciate the Ministry of Science and Technology of Taiwan for funding this study and three anonymous reviewers for their constructive comments.
Abbreviations
- ABySS
Assembly by short sequences
- bp
Base pairs
- CABOG
Celera assembler with the best overlap graph
- Clover
Clustering-oriented de novo assembler
- DNA
Deoxyribonucleic acid
- E-size
Expected size
- GAGE
Genome assembly gold-standard evaluation
- GC-content
Guanine-cytosine content
- kb
Kilo base pairs
- Mb
Mega base pairs
- MSR-CA
Maryland super-read celera assembler
- NGS
Next-generation sequencing
- PCR
Polymerase chain reaction
- rRNA
Ribosomal ribonucleic acid
- SGA
String graphs assembler
- SOAPdenovo
Short oligonucleotide analysis package de novo
- SPAdes
St. Petersburg genome assembler
- tRNA
Transfer ribonucleic acid
Authors' contributions
CYT and MFH: research conception and design; MFH: software development and performance improvement; CLL and MFH: manuscript preparation; CYT and CLL: final approval. All authors read and approved the final manuscript.
Funding
The publication costs of this paper were funded by Ministry of Science and Technology of Taiwan under grant MOST 106-2221-E-126-008.
Availability of data and materials
The evaluation datasets used during the current study are available in the https://gage.cbcb.umd.edu/data/. The source code of Clover is available at https://oz.nthu.edu.tw/~d9562563/src.html.
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Ming-Feng Hsieh, Email: jmfhsieh@gmail.com.
Chin Lung Lu, Email: cllu@cs.nthu.edu.tw.
Chuan Yi Tang, Email: cytang@pu.edu.tw.
Supplementary information
Supplementary information accompanies this paper at 10.1186/s12859-020-03788-9.
References
- 1.Shendure J, Ji H. Next-generation DNA sequencing. Nat Biotechnol. 2008;26:1135–1145. doi: 10.1038/nbt1486. [DOI] [PubMed] [Google Scholar]
- 2.Hawkins RD, Hon GC, Ren B. Next-generation genomics: an integrative approach. Nat Rev Genet. 2010;11:476–486. doi: 10.1038/nrg2795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zerbino DR, Birney E. Velvet: algorithms for de novo short read assembly using de Bruijn graphs. Genome Res. 2008;18:821–829. doi: 10.1101/gr.074492.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kelley DR, Schatz MC, Salzberg SL. Quake: quality-aware detection and correction of sequencing errors. Genome Biol. 2010;11:R116. doi: 10.1186/gb-2010-11-11-r116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li R, Zhu H, Ruan J, Qian W, Fang X, Shi Z, et al. De novo assembly of human genomes with massively parallel short read sequencing. Genome Res. 2010;20:265–272. doi: 10.1101/gr.097261.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Salzberg SL, Phillippy AM, Zimin A, Puiu D, Magoc T, Koren S, et al. GAGE: a critical evaluation of genome assemblies and assembly algorithms. Genome Res. 2012;22:557–567. doi: 10.1101/gr.131383.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Simpson JT, Wong K, Jackman SD, Schein JE, Jones SJ, Birol I. ABySS: a parallel assembler for short read sequence data. Genome Res. 2009;19:1117–1123. doi: 10.1101/gr.089532.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Koren S, Treangen TJ, Pop M. Bambus 2: scaffolding metagenomes. Bioinformatics. 2011;27(21):2964–2971. doi: 10.1093/bioinformatics/btr520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Miller JR, Delcher AL, Koren S, Venter E, Walenz BP, Brownley A, et al. Aggressive assembly of pyrosequencing reads with mates. Bioinformatics. 2008;24(24):2818–2824. doi: 10.1093/bioinformatics/btn548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zimin AV, Marçais G, Puiu D, Roberts M, Salzberg SL, Yorke JA. The MaSuRCA genome assembler. Bioinformatics. 2013;29(21):2669–2677. doi: 10.1093/bioinformatics/btt476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Simpson JT, Durbin R. Efficient de novo assembly of large genomes using compressed data structures. Genome Res. 2012;22:549–556. doi: 10.1101/gr.126953.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bankevich A, Nurk S, Antipov D, Gurevich AA, Dvorkin M, Kulikov AS, et al. SPAdes: a new genome assembly algorithm and its applications to single-cell sequencing. J Comput Biol. 2012;19(5):455–477. doi: 10.1089/cmb.2012.0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shukla SK, Kislow J, Briska A, Henkhaus J, Dykes C. Optical mapping reveals a large genetic inversion between two methicillin-resistant Staphylococcus aureus strains. J Bacteriol. 2009;191(18):5717–5723. doi: 10.1128/JB.00325-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liou ML, Liu CC, Lu CW, Hsieh MF, Chang KC, Kuo HY, et al. Genome sequence of Acinetobacter baumannii TYTH-1. J Bacteriol. 2012;194(24):6974. doi: 10.1128/JB.01860-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen YT, Peng HL, Shia WC, Hsu FR, Ken CF, Tsao YM, et al. Whole-genome sequencing and identification of Morganella morganii KT pathogenicity-related genes. BMC Genomics. 2012;13(Suppl 7):S4. doi: 10.1186/1471-2164-13-S7-S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Clover source code for Linux. Please refer to ‘Installation of Clover’.
Datasets and Installation of Clover. GAGE dataset list and locations, and build Clover’s executing and programming environments.
Section S1—Leptospira shermani assembly statistics results. Section S2—Clover assembly statistics results. Clover output screen text.
Table S1—Memory requirements (GB) of k versus p correlation on Leptospira shermani assembly. Table S2—Sensitivity comparison of different minimum overlapping lengths on Rhodobacter sphaeroides assembly. Supplemental analysis of Clover.
Data Availability Statement
The evaluation datasets used during the current study are available in the https://gage.cbcb.umd.edu/data/. The source code of Clover is available at https://oz.nthu.edu.tw/~d9562563/src.html.


