Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Feb 3.
Published in final edited form as: Nat Methods. 2015 Mar 30;12(5):453–457. doi: 10.1038/nmeth.3337

Robust enumeration of cell subsets from tissue expression profiles

Aaron M Newman 1,2,9, Chih Long Liu 1,2,9, Michael R Green 2,3, Andrew J Gentles 3,4, Weiguo Feng 5, Yue Xu 6, Chuong D Hoang 6, Maximilian Diehn 1,5,7, Ash A Alizadeh 1,2,3,7,8
PMCID: PMC4739640  NIHMSID: NIHMS670442  PMID: 25822800

Abstract

We introduce CIBERSORT, a method for characterizing cell composition of complex tissues from their gene expression profiles. When applied to enumeration of hematopoietic subsets in RNA mixtures from fresh, frozen, and fixed tissues, including solid tumors, CIBERSORT outperformed other methods with respect to noise, unknown mixture content, and closely related cell types. CIBERSORT should enable large-scale analysis of RNA mixtures for cellular biomarkers and therapeutic targets (http://cibersort.stanford.edu).

Changes in cell composition underlie diverse physiological states of metazoans and their complex tissues. For example, in malignant tumors, levels of infiltrating immune cells are associated with tumor growth, cancer progression and patient outcome1,2. Common methods for studying cell heterogeneity, such as immunohistochemistry and flow cytometry, rely on a limited repertoire of phenotypic markers, and tissue disaggregation prior to flow cytometry can lead to lost or damaged cells, altering results3. Recently, computational methods were reported for predicting fractions of multiple cell types in gene expression profiles (GEPs) of admixtures3–9. While such methods perform accurately on distinct cell subsets in mixtures with well-defined composition (e.g., blood), they are considerably less effective for mixtures with unknown content and noise (e.g., solid tumors), and for discriminating closely related cell types (e.g., naïve vs. memory B cells). We present Cell-type Identification By Estimating Relative Subsets Of RNA Transcripts (CIBERSORT), a computational approach that accurately resolves relative fractions of diverse cell subsets in GEPs from complex tissues (http://cibersort.stanford.edu).

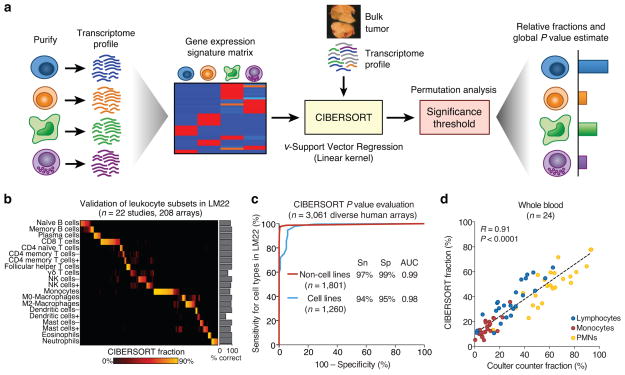
CIBERSORT requires an input matrix of reference gene expression signatures, collectively used to estimate the relative proportions of each cell type of interest. To deconvolve the mixture, we employ a novel application of linear support vector regression (SVR), a machine learning approach highly robust to noise10 (Online Methods and Supplementary Discussion). Unlike previous methods, SVR performs a feature selection, in which genes from the signature matrix are adaptively selected to deconvolve a given mixture (Supplementary Fig. 1). An empirically defined global P value for the deconvolution is then determined (Fig. 1a).

Figure 1.

Figure 1

Open in a new tab

Overview of CIBERSORT and application to leukocyte deconvolution. (a) Schematic of the approach. (b,c) Application of a leukocyte signature matrix (LM22) to deconvolution of (b) 208 arrays of distinct purified or enriched leukocyte subsets (Supplementary Table 2), and (c) 3,061 diverse human transcriptomes. Sensitivity (Sn) and specificity (Sp) in c are defined in relation to positive and negative groups (Online Methods). AUC, area under the curve. (d) CIBERSORT analysis of 24 whole blood samples for lymphocytes, monocytes, and neutrophils compared to measurements by Coulter counter12. Concordance was measured by Pearson correlation (R) and linear regression (dashed line). ‘CIBERSORT fraction’ in b denotes the relative fraction assigned to each leukocyte subset by CIBERSORT. Resting and activated subsets in b are indicated by + and −, respectively.

To assess the feasibility of leukocyte deconvolution from bulk tumors, we designed and validated a leukocyte gene signature matrix, termed LM22. It contains 547 genes that distinguish 22 human hematopoietic cell phenotypes, including seven T cell types, naïve and memory B cells, plasma cells, NK cells, and myeloid subsets (Supplementary Table 1, Supplementary Fig. 2, and Online Methods). Cell subsets can be further grouped into 11 major leukocyte types based on shared lineage (Supplementary Table 1). To validate the gene signatures in LM22, we applied it to deconvolve external datasets of variably purified leukocyte subsets. CIBERSORT results matched ground truth phenotypes in 93% of these datasets (Fig. 1b, Supplementary Fig. 3a, Supplementary Table 2). CIBERSORT also produced results consistent with highly purified T and B cells that we flow-sorted from five human tonsils (Supplementary Fig. 3b).

We next evaluated the CIBERSORT P value metric for sensitivity and specificity by using LM22 to deconvolve 3,061 human transcriptomes11. We first scored expression profiles as ‘positive’ or ‘negative’ depending on the presence or absence of at least one cell type in LM22, respectively. This distinction was considered separately for primary tissue specimens (n = 1,425 positive, 376 negative) and transformed cell lines (n = 118 positive, 1,142 negative). At a P value threshold of ~0.01, CIBERSORT achieved ≥94% sensitivity and ≥95% specificity for distinguishing positive from negative samples (AUC ≥ 0.98; Fig. 1c). Results were similar using an independently derived leukocyte signature matrix4 instead of LM22 (data not shown).

We then benchmarked CIBERSORT on idealized mixtures with well-defined composition4,12,13 (Online Methods), and compared it with six GEP deconvolution methods—linear least squares regression (LLSR)4, quadratic programming (QP)5, PERT6, robust linear regression (RLR), MMAD7 and DSA8 (Supplementary Table 3). CIBERSORT, like other methods, achieved accurate results on idealized mixtures (Supplementary Fig. 4a,b) (Fig. 1d) (Supplementary Table 4). Consequently, we asked whether CIBERSORT might be useful for immune monitoring, and profiled peripheral blood in patients immediately before and after receiving rituximab monotherapy for Non-Hodgkin’s lymphoma. CIBERSORT analysis of post-treatment peripheral blood mononuclear cells (PBMCs) with LM22 revealed a selective depletion of B cells targeted by rituximab in four patients (Supplementary Fig. 4c), suggesting utility for leukocyte monitoring during immunotherapy, especially when specimens cannot be immediately processed.

To compare CIBERSORT’s technical performance with other methods on mixtures with unknown content, we employed commonly used benchmark datasets consisting of four admixed blood cancer cell lines4, each with distinct reference profiles (Supplementary Figs. 5,6 and Online Methods). By combining these mixtures with a colon cancer cell line, we simulated human solid tumors with varying leukocyte infiltration (1% to 100%). We also tested the addition of non-log linear noise to simulate sample handling, stochastic gene expression variation, and platform-to-platform differences. While this simulation framework does not fully reflect biological admixtures of solid tumors, it provided a reasonable model in which unknown content and added noise could be finely tuned and tested.

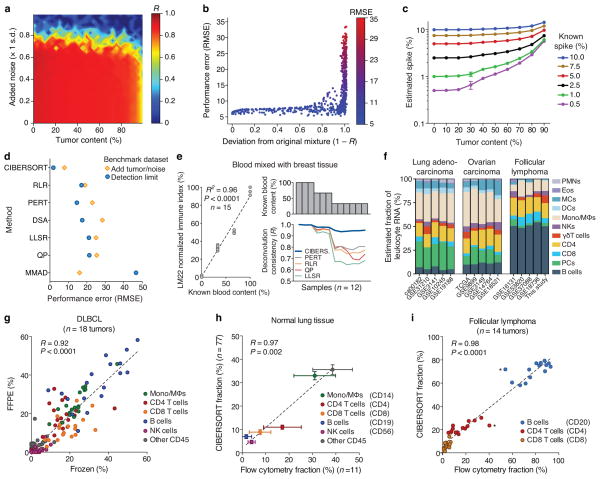
Nearly all methods degraded in performance as a function of signal loss (Supplementary Fig. 5, Supplementary Table 4), showing highly reduced accuracy below 50% immune content. Only CIBERSORT accurately resolved known mixture proportions over nearly the entire range of tumor content (up to ~95%) and noise (up to ~70%) (Fig. 2a), exhibiting strong performance on mixtures that diverged considerably from their original compositions (Pearson’s R as low as ~0.05; Fig. 2b). Since many solid tumor types are composed of fewer than 50% infiltrating immune cells14, the parameter range in which CIBERSORT outperformed other methods is highly relevant for bulk tumor analysis.

Figure 2.

Figure 2

Open in a new tab

Performance assessment on RNA mixtures from complex tissues. (a–c) CIBERSORT accuracy for leukocyte subset resolution in simulated tissues, showing (a) performance across added tumor content (x-axis) and noise (y-axis), (b) deviation of mixtures in a from original values, and (c) detection limits of a given cell type as a function of increasing tumor content (n = 5 random mixtures for each data point). (d) Comparison of six GEP deconvolution methods with CIBERSORT for the analyses shown in a–c (Supplementary Figs. 5,6). (e) Analysis of whole blood spiked into breast tissue. Left: Reported blood proportions versus immune-related gene expression (LM22 normalized immune index; Online Methods). Right: Stability of leukocyte deconvolution across methods. (f) CIBERSORT consistency across independent studies within and across cancer types (for leukocyte abbreviations, see Supplementary Table 1). (g–i) CIBERSORT performance compared between (g) 18 paired frozen and FFPE DLBCL samples, and compared to flow cytometry analysis of (h) 11 normal lung tissues and (i) 14 follicular lymphoma tumors. Asterisks in i indicate potential outliers from the same patient. Surface markers used for quantitation in h and i are indicated in parentheses. Results in e–i were obtained using LM22 and then collapsed into 11 major leukocyte types before analysis (Supplementary Table 1). Concordance was determined by Pearson correlation (R) and linear regression (dashed lines) in e and g–i. Values in c and h are presented as medians ± 95% confidence intervals.

To assess the detection limit of each method for rare cell types in bulk tissues, we created a second synthetic dataset of the same cell lines, but with one blood cell line spiked into random mixtures of the other three blood subsets. CIBERSORT detected cellular fractions down to 0.5% in mixtures containing up to 50% tumor content, and down to 1% in mixtures with over 50% tumor content (Fig. 2c). While all methods overestimated spike-ins with higher tumor content, the effect was least pronounced for CIBERSORT (Supplementary Fig. 6). Overestimation was less common in a separate analysis, in which each cell type in LM22 was spiked into random combinations of the remaining 21 subsets over a range of unknown content (Supplementary Fig. 7). Overall, CIBERSORT consistently outperformed other methods, substantially in some cases (Fig. 2d, Supplementary Figs. 5–7, and Supplementary Table 4).

We next investigated CIBERSORT’s discriminatory ability on cell types with correlated GEPs, which can be difficult to resolve in mixtures due to multicollinearity15. Previous approaches avoid this issue by using cell type-specific marker genes7,8,13 or highly distinct GEPs4,5. In contrast, CIBERSORT does not require cell type-specific expression for every gene, suggesting applicability to diverse cell phenotypes (Supplementary Fig. 8). In addition, despite performing a feature selection on signature matrix genes (Supplementary Fig. 1), we did not observe any effect of the choice of genes on deconvolution of closely related cell types (Supplementary Fig. 9, Supplementary Results). When compared to other methods on synthetic mixtures of increasingly correlated cell types, CIBERSORT performed most accurately (Supplementary Fig. 10), demonstrating potential for deep deconvolution of many cell subsets3.

Having benchmarked CIBERSORT on simulated mixtures, we next focused on in vitro and in vivo mixtures of solid tissues, including bulk tumors. We used LM22 for all remaining analyses and restricted our comparative assessments to expression-based methods (RLR, PERT, QP, and LLSR). First, we tested deconvolution stability in a spike series of whole blood added to breast tissue5. After verifying relative spike-in proportions by comparison with immune-related gene expression (Fig. 2e), we found that CIBERSORT was significantly more consistent than other methods (P < 0.02; n = 9 samples with <100% blood; paired two-sided Wilcoxon signed rank test; Fig. 2e; Supplementary Table 4). Separately, across independent studies, leukocyte fractions enumerated by CIBERSORT were more similar within a cancer type than across cancers (Fig. 2f). These results indicate that unknown content and lab-specific factors only marginally impact CIBERSORT performance.

We next applied CIBERSORT to formalin-fixed, paraffin embedded (FFPE) samples. Using publicly available GEPs of matching FFPE and frozen DLBCL tumors16, we found that leukocyte fractions estimated by CIBERSORT were significantly correlated across all tumors (Fig. 2g) and were more concordant than other methods (Supplementary Table 4). Indeed, CIBERSORT results were also significantly correlated in 16 of 18 individual tumors (P < 0.05; Supplementary Fig. 11a) and in specific cell subsets (Supplementary Fig. 11b), implying potential utility for large-scale analysis of cellular composition in FFPE specimens.

To evaluate CIBERSORT against ground truth measurements of leukocyte content in solid tissues, we used flow cytometry to enumerate immune subsets in two tissue types: lung specimens obtained during surgical resection of early stage non-small cell lung carcinomas, and disaggregated lymph node biopsies from follicular lymphoma (FL) patients. Whether applied to (i) independent microarray studies of normal lung tissues or (ii) GEPs from 14 paired bulk FL samples, results were significantly correlated with corresponding flow cytometry measurements (P ≤ 0.005, Fig. 2h,i, respectively) and in both tissue types, more closely reflected experimental values than previous methods (Supplementary Table 4).

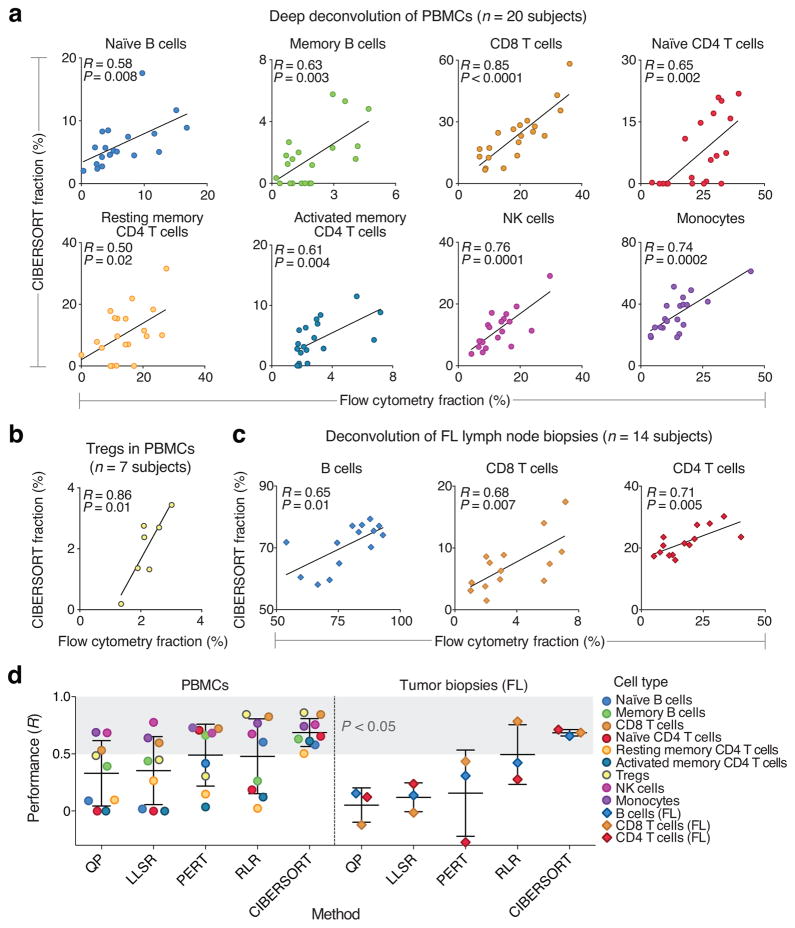
To assess performance on individual cell subsets, we used flow cytometry to enumerate nearly 50% of the phenotypic repertoire of LM22 (10 of 22 cell subsets), and evaluated CIBERSORT’s capability for deep deconvolution in PBMCs and tumor biopsies. Blood samples from 27 adult subjects were profiled for ten phenotypes captured in LM22 (20 subjects were profiled for nine cell types, and seven profiled for FOXP3+ Tregs; Supplementary Note). Of these ten phenotypes, half are highly collinear in LM22 (Supplementary Fig. 2c) and half have low median frequencies (<5%) in PBMCs (Supplementary Note). Despite the diversity of phenotypes analyzed, 90% of distinct leukocyte subsets were significantly correlated between CIBERSORT and flow cytometry (P ≤ 0.02; Fig. 3a), including four of five subsets with median fractions below 5% (e.g., Tregs; Fig. 3b). Only gamma delta T cells were not significant (albeit positively correlated; R = 0.29), possibly due to technical issues with flow cytometry or the use of a suboptimal reference profile (Supplementary Fig. 3a). Separately, in FL tumor biopsies, CD4 and CD8 T cells and malignant B cells were each significantly correlated between CIBERSORT and flow cytometry (P ≤ 0.02; Fig. 3c).

Figure 3.

Figure 3

Open in a new tab

Deep deconvolution and enumeration of individual cell subsets in 41 human subjects. (a–c) Direct comparison between CIBERSORT and flow cytometry for: (a) the indicated eight immune cell subsets in PBMCs from 20 subjects, (b) FOXP3+ Tregs in PBMCs from seven subjects, and (c) the indicated three immune cell subsets in lymph node biopsies from 14 subjects with follicular lymphoma (FL). Concordance was determined by Pearson correlation (R) and linear regression (solid lines). (d) Comparison of five expression-based deconvolution methods on the datasets analyzed in a–c. The shaded gray area denotes deconvolved cell types that significantly correlated with flow cytometry (P < 0.05, Pearson correlation). Scatterplots and RMSE values for all methods are provided in the supplement (Supplementary Figs. 12, 13 and Supplementary Table 4, respectively). In three instances, correlation coefficients could not be determined; these were assigned a value of zero for inclusion in this panel (Supplementary Table 4, Supplementary Fig. 12). Data are presented as means ± standard deviations.

When applied to the same datasets using LM22, other expression-based methods were generally less accurate, and none yielded significant correlations for >50% of analyzed phenotypes (Fig. 3d, Supplementary Figs. 12,13, and Supplementary Table 4). Moreover, certain subsets were observed to ‘drop out’ when enumerated by other methods, likely owing to multicollinearity (e.g., naïve CD4 T cell levels estimated by QP and LLSR in PBMCs; Fig. 3d, Supplementary Figs. 12,13). Furthermore, for FL tumor biopsies, significant correlations were only achieved by other methods when all leukocyte subsets were evaluated together, not separately (except for CD8 T cells inferred by RLR; Supplementary Fig. 13). Potential reasons for these performance differences are discussed in Online Methods and Supplementary Discussion. Collectively, these results further demonstrate the advantages of CIBERSORT for deep deconvolution and enumeration of cell subsets in tissues with complex compositions.

To summarize, we present CIBERSORT for characterizing cell heterogeneity using RNA mixtures from nearly any tissue. CIBERSORT exhibits substantially improved accuracy for the analysis of mixtures with (i) noise or unknown content and (ii) closely related cell types (Supplementary Fig. 14). When applied with statistical filtration, CIBERSORT coupled with LM22 allows for highly sensitive and specific discrimination of human leukocyte subsets. We note that our filtration approach is likely applicable to other signature matrices and other GEP deconvolution methods.

The most significant current limitation of CIBERSORT, and indeed all signature gene-based methods, is the fidelity of reference profiles, which could deviate in cells undergoing heterotypic interactions, phenotypic plasticity, or disease-induced dysregulation. Sampling a larger expression space by sorting populations from diverse physiological conditions (e.g., specific tumor-infiltrating immune cells) may mitigate this issue. Second, CIBERSORT currently does not provide P values for detection limits of individual cell types. Third, despite a considerably lower estimation bias than other approaches, some cell types were systematically over- or under-estimated by CIBERSORT (see RMSE values in Supplementary Table 4); efforts to address this are underway. Finally, while CIBERSORT was not explicitly tested on RNA-Seq data, the linearity assumptions made by our method are likely to hold, as previously suggested17.

We anticipate that CIBERSORT will prove valuable for analysis of cellular heterogeneity in microarray or RNA-Seq data derived from fresh, frozen, and fixed specimens, thereby complementing methods that require living cells as input.

Online Methods

Patient samples

All patient samples in this study were reviewed and approved by the Stanford Institutional Review Board in accordance with the Declaration of Helsinki. Tonsils were collected as part of routine tonsilectomy procedures at Lucile Packard Children’s Hospital at Stanford University with informed consent for research use, and then mechanically disaggregated before cell suspensions were cryopreserved (Supplementary Fig. 3b). Peripheral blood mononuclear cells (PBMCs) were isolated from specimens taken before and immediately following four weekly doses of infusional rituximab (375 mg m−2) monotherapy for extranodal marginal zone lymphoma (EMZL) in a subject without measurable circulating disease (patient 1 in Supplementary Fig. 4c). PBMCs were respectively isolated from specimens taken immediately following four cycles and six cycles of RCHOP immunochemotherapy for treatment of DLBCL (patients 2 and 3 in Supplementary Fig. 4c). PBMCs were also isolated from a subject following four cycles of Rituximab for treatment of FL (patient 4 in Supplementary Fig. 4c); this subject had ~2% circulating lymphoma cells at diagnosis, which were undetectable by CIBERSORT and flow cytometry following four Rituximab infusions. Specimens of adjacent normal lung tissue were obtained during surgical resection of early stage non-small cell lung tumors (Fig. 2h). Surgical tissue biopsies were obtained from untreated FL patients enrolled in a Phase III clinical trial (NCT0001729018) (Fig. 2i and Fig. 3c). Lastly, PBMCs were obtained from 20 adults of varying ages receiving influenza immunization (NCT01827462) (Fig. 3a), and from seven adults consisting of patient 4 in Supplementary Fig. 4c and six healthy subjects (Fig. 3b, which includes patient 4).

Flow cytometry

Details are provided in the supplement (Supplementary Note and Supplementary Results).

Gene expression profiling

Nucleic acids were extracted from tonsil specimens (Supplementary Fig. 3b) and PBMCs (patients 1 to 3 in Supplementary Fig. 4c) using AllPrep DNA/RNA Mini kits (Qiagen). For FL specimens (Fig. 2i, Fig. 3c), total RNA and genomic DNA were prepared and stored using TRIzol and RNeasy Midi Kits (Qiagen). Sufficient nucleic acid was confirmed for 80% of archival FL specimens after quality control assessment of a subset of these patients. Total RNA from FL samples was linearly amplified (3′ IVT Express, Affymetrix) prior to microarray hybridization. For all above samples, total cellular RNA (at least 300 ng) was assessed for yield (NanoDrop 2000, Thermo Scientific), and quality (2100 Bioanalyzer, Agilent), and cRNA was hybridized to HGU133 Plus 2.0 microarrays (Affymetrix) according to the manufacturer’s protocol.

Two additional cohorts of PBMCs were analyzed in this study (Fig. 3a,b). For the first cohort (n = 20 subjects; Fig. 3a), PBMCs (~1×106 viable cells per mL) were collected in 1 mL TRIzol (Invitrogen) and stored at −80 °C until use. Total RNA was isolated according to the TRIzol protocol (Invitrogen). Total RNA yield was assessed using the Thermo Scientific NanoDrop 1000 micro-volume spectrophotometer (absorbance at 260 nm and the ratio of 260/280 and 260/230). RNA integrity was assessed using a Bioanalyzer NANO Lab-on-a-Chip instrument (Agilent). Biotinylated, amplified antisense complementary RNA (cRNA) targets were prepared from 200 to 250 ng of total RNA using the Illumina RNA amplification kit (Life Technologies), and 750 ng of labeled cRNA was hybridized overnight to Human HT-12 V4 BeadChip arrays (Illumina). The arrays were then washed, blocked, stained and scanned on an Illumina BeadStation 500 following the manufacturer’s protocols. GenomeStudio software version 1.9.0 (Illumina) was used to generate signal intensity values from the scans. For the second cohort (Fig. 3b), PBMCs (1.4×106 to 4.0×106 cells per mL) from six healthy male adults were isolated and prepared as described in Supplementary Note and then frozen at −80 °C until use. Total cellular RNA ≥300 ng) was isolated from these six subjects along with viably preserved PBMCs from patient 4 (Supplementary Fig. 4c) using RNeasy Mini Kit (Qiagen) and assessed for yield (NanoDrop 2000, Thermo Scientific), and quality (2100 Bioanalyzer, Agilent). Total RNA was linearly amplified (3′ IVT Express, Affymetrix), and cRNA was hybridized to HGU133A microarrays (Affymetrix) according to the manufacturer’s protocol.

Overview of CIBERSORT

Deconvolution model

A variety of GEP deconvolution methods have been proposed, most of which model an mRNA mixture m by a system of linear equations, corresponding to a weighted sum of cell type-specific GEPs3–9,12,13,17,19. Let B denote a GEP signature matrix and let f denote a vector consisting of the unknown fractions of each cell type in the mixture. Then the problem of GEP deconvolution can be represented by m = f x B, provided that B contains more marker genes than cell types (i.e., the system is overdetermined4). The preponderance of genes in whole transcriptome studies renders this requirement trivial in practice. If the linearity argument is biologically plausible, as previous studies imply4,12,13,20, then genes with expression profiles enriched in each cell type can be leveraged to impute unknown cell fractions from mixture profiles5.

Signature matrix

Matrices of cell-specific expression signatures—termed base or basis matrices in prior studies4,5,19—can be obtained by differential expression analysis of purified or enriched cell populations. Gene signature matrices can be made more robust by minimizing an inherent matrix property called the condition number, which measures the stability of the linear system to input variation or noise4,5. In this work, we measure signature matrix stability via the 2-norm condition number, calculated with the kappa function in R. The specific steps used to build LM22 are described in ‘LM22 signature matrix’.

The process of building a signature matrix represents a type of ‘filter method’, a preprocessing step that removes irrelevant features prior to application of a specific machine learning approach or prediction algorithm21. Specifically, the use of a signature matrix facilitates (1) faster computational running time owing to the elimination of genes with uniform expression levels across the cell types of interest (e.g., housekeeping genes and unexpressed genes), and (2) a greater signal to noise ratio by preselecting reference profiles that have maximal discriminatory power (as measured by condition number). While several previous expression-based methods rely on feature selection to build a signature matrix for deconvolution (e.g., LLSR and QP), to our knowledge, this is the first work to incorporate an additional round of feature selection to adaptively select genes from an existing signature matrix (detailed below).

Support vector regression (SVR)

To address limitations of previous methods (Supplementary Discussion), we propose a new approach for Cell Type Identification By Estimating Relative Samples Of RNA Transcripts (CIBERSORT). Our strategy is based on a novel application of nu-support vector regression (ν-SVR)10, a machine-learning method that outperformed other approaches in benchmarking experiments (Supplementary Fig. 14, Supplementary Table 4). ν-SVR is an instance of support vector machine (SVM), a class of optimization methods for binary classification problems, in which a hyperplane is discovered that maximally separates both classes. The support vectors are a subset of the input data that determine hyperplane boundaries. Unlike standard SVM, SVR discovers a hyperplane that fits as many data points as possible (given its objective function10) within a constant distance, ε, thus performing a regression (Supplementary Fig. 1). All data points within ε (termed the ‘ε-tube’) are ignored (open circles in Supplementary Fig. 1, left panel), whereas all data points lying outside of the ε-tube are evaluated according to a linear ε-insensitive loss function10. These outlier data points, referred to as ‘support vectors’ (red circles in Supplementary Fig. 1), define the boundaries of the ε-tube and are sufficient to completely specify the linear regression function. In this way, support vectors can provide a sparse solution to the regression in which overfitting is minimized (a type of feature selection). Notably, support vectors represent genes selected from the signature matrix in this work.

The primal objective of SVR is to minimize both a loss function and penalty function given a defined set of constraints. The former measures the error associated with fitting the data whereas the latter determines model complexity. More specifically, SVR solves an optimization problem that minimizes the following two quantities10: (1) a linear ε-insensitive loss function, which outperforms other common loss functions (e.g., squared error used in LLSR) in noisy samples22, and (2) an L2–norm penalty function (the same as that used in ridge regression23), which penalizes model complexity while minimizing the variance in the weights assigned to highly correlated predictors24,25 (e.g., closely related cell types), thereby combating multicollinearity. For further details, see ref. 10.

Two major types of SVR have been described, ε-SVR26 and ν-SVR10, however we applied ν-SVR in CIBERSORT since the ν parameter conveniently imparts both an upper bound on training errors and a lower bound on support vectors10. Higher values of ν yield narrower ε-tubes and consequently, more support vectors10 (Supplementary Fig. 1). For CIBERSORT, ν-SVR is applied with a linear kernel to solve for f, and the best result from three values of ν = {0.25, 0.5, 0.75} is saved, where ‘best’ is defined as the lowest root mean squared error between m and the deconvolution result, f x B. Our current implementation of CIBERSORT executes ν-SVR using the ‘svm’ function in the R package, ‘e1071’. Regression coefficients are extracted with the following R command:

coef <- t(model$coefs) %*% model$SV

Negative SVR regression coefficients are subsequently set to zero (as done for LLSR), and the remaining regression coefficients are normalized to sum to 1, yielding a final vector of estimated cell type fractions, f (notably, f denotes relative, not absolute fractions of each cell type from B in m). To decrease running time and promote better overall performance, both B and m are each normalized to zero mean and unit variance prior to running CIBERSORT. As previously suggested for other linear deconvolution methods, CIBERSORT works best on expression values in non-log linear space20.

Taken together, linear ν-SVR as implemented by CIBERSORT, uniquely addresses key outstanding issues of gene expression deconvolution (see Supplementary Discussion), including (1) robustness to noise and overfitting owing to both a linear loss function22 and feature selection of genes from the signature matrix, and (2) tolerance to multicollinearity via utilization of the L2-norm penalty function25. Moreover, CIBERSORT does not require cell type-specific expression patterns for every gene, allowing the construction of signature matrices with more cell types and phenotypic states than other methods (Supplementary Fig. 8).

P-value estimation

In contrast to previous methods, CIBERSORT produces an empirical P value for the deconvolution using Monte Carlo sampling. This approach allows CIBERSORT to test the null hypothesis that no cell types in the signature matrix (e.g., LM22) are present in a given GEP mixture, m. For this purpose, we use the Pearson product-moment correlation R calculated between m and f x B as the test statistic, though other distance metrics could be used. In order to derive an empirical P value, CIBERSORT must first derive a null distribution R*. Because the signature matrix B will contain only a small subset of genes g compared to the whole transcriptome, g expression values are randomly drawn from the parent GEP of m to create a random mixture m*i, such that |m| = |m*i|. CIBERSORT is then run on m*i to produce a vector of estimated cellular fractions, f*i. CIBERSORT determines the correlation coefficient R*i between the random mixture m*i and the reconstituted mixture, f*i x B. This process is repeated for I iterations (=500 in this work) to produce R*.

Running time

Using three threads to simultaneously process three values of ν (0.25, 0.5, and 0.75), and a 2.3 GHz Intel Core i7 CPU with 8 GB RAM, we clocked CIBERSORT runtime with LM22 at approximately 1.7 sec per mixture sample after an empirical P value was calculated. The latter depends on the number of permutations selected, and for 100x, would take ~170 sec, or an additional 2.75 min.

Implementation and website

CIBERSORT was developed in Java and R with a simple command-line interface for processing gene expression data representing a mixture of different cell types, along with a signature genes file that enumerates the genes that define the signature expression profile for each cell type. Given these data, the tool generates the fractional representations of each cell type present in the mixture and returns it to the website to be rendered as a heat map table and stacked bar plot representations. The application can also produce custom signature gene files when provided with gene expression profiles of reference cell populations and a class comparison table for those populations.

The back end website for CIBERSORT was built in PHP. The interactive user interface is powered by the jQuery JavaScript library and various open source libraries (including phpMailer, idiorm, blueimp jQuery-File-Upload, DataTables, phpExcel and mPDF), with the graphical user interface of the website powered by Twitter Bootstrap 2.3.2. The site runs on an Apache server on a virtual machine and stores user and job data in a MySQL database. However, the user has complete control over their data and can delete them at will. The CIBERSORT website is hosted at http://cibersort.stanford.edu, and includes datasets used for benchmarking, tutorials for the use of CIBERSORT and preparation of input data, downloadable software and source code, and example files.

Other GEP deconvolution methods

We compared CIBERSORT results with six GEP deconvolution methods—four that take reference expression profiles as input: linear least squares regression (LLSR)4, quadratic programming (QP)5, PERT6, and robust linear regression (RLR); and two that take genes uniquely expressed in a given cell type as input (i.e., marker genes): MMAD7 and DSA8 (Supplementary Table 3). To the best of our knowledge, RLR was first applied to GEP deconvolution in this work. LLSR, QP, RLR and DSA were run in R using ‘stats’ (‘lm’ function), ‘quadprog’, ‘MASS’ (‘rlm’ function, 100 maximum iterations), and ‘DSA’8 packages, respectively. Negative coefficients from LLSR were set to zero to approximate the approach used by Abbas et al.4, and QP was run with non-negativity and sum to 1 constraints used by Gong et al.5,17. MMAD and PERT were run in Matlab using author-supplied code6,7 (PERT was converted from Octave using the Matlab converter, ‘oct2ml’). PERT was assessed using the same signature gene matrices used for the other expression-based methods. MMAD was evaluated using marker genes only, as this approach yielded superior results when compared to expression-based deconvolution (Fig. 3C vs. Fig. 3A in Liebner et al.7). However, cell-specific marker genes could not be determined for all cell types in LM22, and therefore, MMAD and DSA were not run on datasets where LM22 was applied. All methods were run in non-log linear space.

Microarray datasets and preprocessing

Samples profiled on Illumina or Agilent platforms in Fig. 1b (and Supplementary Table 2) were downloaded as normalized matrices from public repositories (either NCBI, EBI, or literature; referenced in Supplementary Table 2), and probes were converted to HUGO gene symbols using chipset definition files available from the NCBI gene expression omnibus (GEO). Human transcriptome data11 from Fig. 1c were downloaded as RMA-normalized arrays (E-MTAB-62, EBI ArrayExpress). Other Affymetrix arrays were obtained as CEL files, MAS5 normalized using the ‘affy’ package in Bioconductor, mapped to NCBI Entrez gene identifiers using a custom chip definition file (Brainarray version 12.1.0; http://brainarray.mbni.med.umich.edu/Brainarray/; also available at http://cibersort.stanford.edu), and converted to HUGO gene symbols. The Illumina BeadChip arrays analyzed in Fig. 3a were normalized with limma v3.20.8 (Bioconductor) using ‘normexp’ background correction with negative controls (‘neqc’ function). For non-Affymetrix platforms, genes mapping to >1 probe were collapsed at the gene-level according to the probe with highest mean expression across all samples. All microarray studies were quantile normalized prior to analysis. For normal lung tissues in Fig. 2h, we analyzed GEO datasets, GSE767027 and GSE1007228, and for paired frozen and FFPE samples of DLBCL tumors in Fig. 2g, we analyzed GSE1837716.

LM22 signature matrix

We obtained GEP data from the public domain for 22 leukocyte subsets profiled on the HGU133A platform (Supplementary Table 1). Probesets were preprocessed as described above. Significantly differentially expressed genes between each population and all other populations were identified using a two-sided unequal variance t-test. Genes with a q-value < 0.3 (false discovery rate29) were considered significant.

For each leukocyte subset, significant genes were ordered by decreasing fold change compared to other cell subsets, and the top G marker genes from each cell subset were combined into a signature matrix BG. We iterated G from 50 to 200 across all subsets, and retained the signature matrix with the lowest condition number (condition number = 11.4; G = 102; n = 547 distinct genes; Supplementary Table 1).

To prevent genes expressed on non-hematopoietic cell types from confounding deconvolution results, we also used two gene filtration strategies. First, we identified genes with enriched expression in non-hematopoietic cells or tissues using the Gene Enrichment Profiler, an online compendium of diverse cells and tissues profiled on HGU133A (http://xavierlab2.mgh.harvard.edu/EnrichmentProfiler/)30. Gene Enrichment Profiler calculates an enrichment score (ES) for a given gene in a given cell or tissue type based on the sum of linear model coefficients from all pairwise comparisons of that gene with other samples. For each gene and cell or tissue type with ES > 0, we determined the fraction of non-hematopoietic cell or tissue samples in the Gene Enrichment Profiler database, and excluded genes from the signature matrix with a non-hematopoietic fraction >0.05. As a second filtration step, we omitted all genes from further analysis with a mean log2 expression level ≥7 in all non-hematopoietic cancer cell lines profiled in the Cancer Cell Line Encyclopedia (CCLE) (pre-normalized gene expression data were extracted from CCLE_Expression_Entrez_2012-09-29.txt, downloaded from the Broad Institute). We termed the final signature matrix ‘LM22’.

To validate the gene signatures used to distinguish each leukocyte subset in LM22, we applied CIBERSORT to a variety of external datasets, each containing one purified population also present in the signature matrix. We tested GEPs from three microarray platforms, Affymetrix HGU133A and HGU133 Plus 2.0, and the Illumina Human-6 v2 Expression BeadChip. Affymetrix platforms were normalized and processed the same as described for signature matrix GEPs. The BeadChip dataset was downloaded as a processed normalized matrix from ArrayExpress (E-TABM-63331), and for genes mapped to more than one probe, the probe with highest mean expression across all samples was further analyzed. For each sample, the population with the highest CIBERSORT-inferred fraction was compared to the known cell type to assess CIBERSORT accuracy (Supplementary Table 2).

For the analysis presented in Fig. 1c, arrays were grouped into 1,801 primary human specimens, consisting of 1,425 ‘positive’ samples containing at least one mature hematopoietic subset in LM22 and 376 ‘negative’ samples containing incompletely differentiated non-hematopoietic specimens, normal brain tissue (which typically contains microglia, but generally not cell types in LM22), and hematopoietic stem cells and progenitors (not in LM22). Arrays were separately grouped into 1,260 transformed cell lines, divided into 118 ‘positive’ hematopoietic samples and 1,142 ‘negative’ samples, the latter consisting of both non-hematopoietic samples and K562 erythromyeloblastoid cell lines, which are hematopoietic in origin but highly distinct from subsets present in LM22. Poorly annotated arrays were excluded from this analysis. While significance filtering was not applied in comparing CIBERSORT to other methods, we imposed a P value cutoff (≤0.01; see Fig. 1c) for deconvolution of bulk tumors (Fig. 2f).

Other signature matrices

In addition to LM22, custom signature matrices were designed for mixtures of hematopoietic cell lines and neural populations (Supplementary Fig. 4a,b). In both cases, previously normalized series matrix datasets (GSE111034 and GSE1938013) were downloaded from GEO and quantile normalized. Signature matrices were subsequently constructed using the same condition number minimization algorithm described for LM22 (above), omitting non-hematopoietic gene filtration and validation steps. The final signature matrices for GSE11103 and GSE19380 were comprised of 584 probesets (condition number = 1.86) and 280 probesets (condition number = 1.8), respectively. To compare CIBERSORT performance with marker gene-based methods (as in Supplementary Table 4), we defined marker genes from each signature matrix by selecting all genes with at least five-fold higher expression in one cell type compared to the others (as in ref. 7).

Statistical analysis

Unless stated otherwise, concordance between known and predicted cell type proportions was determined by Pearson correlation coefficient (R) and Root Mean Squared Error (RMSE) to measure linear fit and estimation bias, respectively. Importantly, the latter was calculated on cell type proportions represented as percentages. Group comparisons were determined using a two-sided Wilcoxon test, unpaired or paired, as appropriate. All results with P < 0.05 were considered significant. Statistical analyses were performed with R and Prism v6.0d (GraphPad Software, Inc.).

Analysis of idealized mixtures

Unlike complex mixtures, idealized mixtures are defined in this work as having well-defined composition, in which the majority of the mixture can be accounted for by highly distinct (uncorrelated) reference profiles of purified cell types, and the contribution from unknown cell content and noise is minimal. CIBERSORT exhibited comparable performance to other methods on idealized mixtures, such as in vitro mixtures of blood cancer cell lines4 and neural cell types13 (Supplementary Fig. 4a,b), and whole blood12 (Fig. 1d) (Supplementary Table 4).

Analysis of simulated tumors with added noise

We benchmarked CIBERSORT against six GEP deconvolution methods (RLR and five others4–8) by comparing their results on mixtures with different levels of unknown content (i.e., tumor) and noise. To facilitate a fair comparison, we used previously defined in vitro mixtures (n = 12) of four blood cell lines (GSE11103), each of which is highly distinct and readily deconvolved (Supplementary Fig. 4a). To evaluate expression-based methods, we used a signature matrix with nearly 600 distinguishing genes (described above and applied in Supplementary Fig. 4a), whereas for marker-based deconvolution, we selected marker genes as described above (n = 500 genes). To simulate tumors with infiltrating leukocytes, we combined the cell line mixtures with defined inputs of a GEP from a colon cancer cell line (HCT116), calculated as the mean of two replicate arrays (GSM269529 and GSM269530; GSE10650). Both GSE11003 and GSE10650 datasets were MAS5 and quantile normalized together prior to analysis. To introduce noise, we added values randomly sampled from the following distribution, 2^N(0, f × σ), with f in the range [0,1) (i.e., y-axis in Fig. 2a and Supplementary Fig. 5a), and σ set to the global standard deviation across the original mixtures represented in log2 space (=11.6). Since GSE11103 consists of four distinct mixtures with three replicates each, we measured the performance of each algorithm over the entire set of 12 mixtures (R and RMSE; Supplementary Fig. 5, Supplementary Table 4). Moreover, we independently iterated over tumor content (0% to <100%) and noise (f, [0,1)) in 30 regularly spaced intervals, such that together, 900 sets of mixtures were analyzed.

Analysis of cell subset detection limit

We performed two in silico experiments to assess the detection limits of different deconvolution algorithms. In the first experiment (Supplementary Fig. 6), we used the same cell line GEPs described above to compare CIBERSORT and RLR with five other GEP deconvolution methods4–8. We evaluated detection limit using Jurkat cells (spike-in concentrations of 0.5%, 1%, 2.5%, 5%, 7.5%, and 10%), whose reference GEP (median of three replicates in GSE11103) was added into randomly created background mixtures of the other three blood cell lines. Five mixtures were created for each spike-in concentration. Predicted Jurkat fractions were assessed in the presence of differential tumor content, which we simulated by adding HCT116 (described above) in ten even increments, from 0% to 90%. Of note, we also used the same marker or signature genes described for simulated tumors (above). In a second experiment (Supplementary Fig. 7a), we compared CIBERSORT with QP5, LLSR4, PERT6, and RLR. We spiked naïve B cell GEPs from the leukocyte signature matrix into four random background mixtures of the remaining 21 leukocyte subsets in the signature matrix. The same background mixtures were used for each spike-in. We also tested the addition of unknown content by adding defined proportions (0 to 90%) of randomly permuted expression values from a naïve B cell reference transcriptome (median expression profile from samples used to build LM22, Supplementary Table 1). We then repeated this analysis for each of the remaining leukocyte subsets in LM22 (Supplementary Fig. 7b).

Analysis of cell type-specific marker genes

Cell type-specific marker genes may be difficult if not impossible to ascertain between closely related cell types. As such, we tested whether marker genes expressed by >1 cell type in the signature matrix could still be useful to CIBERSORT, provided that each reference profile in the signature matrix remains unique. We created two artificial signature matrices (containing ten genes and five cell types each) representing opposite extremes: one containing only cell type specific genes (called SM1; Supplementary Fig. 8a) and the other without any cell type specific genes (called SM2; Supplementary Fig. 8b). Of note, unlike signature matrices derived from real expression data, SM1 and SM2 are fully defined and therefore ideally suited for this analysis. Moreover, reference profiles in SM2 are highly inter-correlated, as might be expected for subsets without unique marker genes. We generated random mixing proportions according to a uniform distribution, and combined the cell types in each signature matrix to create ten mixtures. We then added low-level noise by randomly shuffling genes in one of the mixtures and combining 5% of the resulting vector with 95% of each of the ten mixtures. CIBERSORT and DSA were compared using SM1 (Supplementary Fig. 8c), and CIBERSORT, RLR, QP, LLSR, and PERT were compared using SM2 (Supplementary Fig. 8d,e). While CIBERSORT performed identically to DSA on SM1, it was substantially more accurate than other methods on SM2, closely approximating its performance on SM1 (Supplementary Fig. 8d,e). This analysis demonstrates CIBERSORT’s softer dependency on cell type specific signature matrix genes, an important requirement for deep deconvolution3.

Analysis of multicollinearity

We compared CIBERSORT with three signature gene expression-based deconvolution methods, QP5, LLSR4, and RLR (this work), for the impact of multicollinearity (i.e., the degree of inter-sample correlation in the signature matrix) on mixtures with unknown content (i.e., parts of the mixture unaccounted for in the signature matrix), and noise added to either B or m. Random signature matrices were created from 41 naïve B cell signature genes (derived from GSE2288632) by randomly selecting and permuting P gene expression values from the original non-random set of 41 genes, thus maintaining realistic gene expression distributions (n = 10 populations). The number of genes P was used to control multicollinearity within the signature matrix (higher P = less collinear, and vice versa), and for each P, ten random signature matrices were generated. Simulated mixtures were created by randomly apportioning populations from the signature matrix. To simulate unknown content (Supplementary Fig. 10a–c), three concentrations (5%, 25%, and 50%) of ten additional cell populations were randomly combined and added to each mixture. Non-log linear noise was additively introduced into simulated mixtures (Supplementary Fig. 10d) by randomly sampling from 2^N(0, j) (the exponent denotes a normal distribution with mean of zero and standard deviation j). Under all conditions tested, CIBERSORT outperformed the other three methods.

Analysis of deconvolution consistency

We applied LM22 to a publicly available dataset (GSE298325) to measure stability of deconvolution results over defined levels of blood admixed with breast tissue. To confirm reported fractions of blood admixed with breast tissue, we compared these proportions with an ‘LM22 normalized immune index’, defined for each sample as the median gene expression value of all genes in LM22 (Supplementary Table 1) divided by the median expression level of the transcriptome, and normalized into the range of known leukocyte content across the datasets (Fig. 2e). As a consistency metric, we compared deconvolution results for each sample with results from the sample with highest immune purity (Fig. 2e).

Supplementary Material

1
2
3
4
5

Acknowledgments

We are grateful to H. Maecker, M. Davis, R. Levy, and the Stanford Human Immune Monitoring Center for assistance with this study. This work was supported by grants from the Doris Duke Charitable Foundation (A.A.A.), the Damon Runyon Cancer Research Foundation (A.A.A.), the B&J Cardan Oncology Research Fund (A.A.A.), the Ludwig Institute for Cancer Research (A.A.A. and M.D.), US National Institutes of Health (NIH) grant U01 CA154969 (A.J.G., W.F., Y.X., C.D.H., and M.D.), NIH grant U19 AI090019, NIH grant 5T32 CA09302-35 (A.M.N.), US Department of Defense grant W81XWH-12-1-0498 (A.M.N.), and a grant from the Siebel Stem Cell Institute and the Thomas and Stacey Siebel Foundation (A.M.N.).

Footnotes

Accession codes Gene expression data from this work have been deposited in the Gene Expression Omnibus with accession code GSE65136.

Author Contributions A.M.N. and A.A.A conceived of CIBERSORT, developed strategies for related experiments, analyzed the data and wrote the paper. A.M.N. developed and implemented CIBERSORT. C.L.L. implemented web infrastructure and wrote the paper. M.R.G. performed flow cytometry and gene expression profiling of leukocytes from human tonsils and peripheral blood. A.J.G assisted in the conceptual development of CIBERSORT. W.F., Y.X., C.D.H. and M.D. assisted in the collection and analysis of lung tissue. All authors discussed the results and implications and commented on the manuscript at all stages.

Competing Financial Interests

The authors declare no competing financial interests.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS670442-supplement-1.pdf (160.5KB, pdf)
2
NIHMS670442-supplement-2.xlsx (267.4KB, xlsx)
3
NIHMS670442-supplement-3.xlsx (19.6KB, xlsx)
4
NIHMS670442-supplement-4.xlsx (46.6KB, xlsx)
5
NIHMS670442-supplement-5.xlsx (58.4KB, xlsx)

RESOURCES