Summary
The great epidemic of poliomyelitis which swept New York City and surrounding territory in the summer of 1916 eclipsed all previous global experience of the disease. We draw on epidemiological information that is included in the seminal US Public Health Bulletin 91, ‘Epidemiologic studies of poliomyelitis in New York City and the northeastern United States during the year 1916’ (Washington DC, 1918), to re-examine the spatial structure of the epidemic. For the main phase of transmission of the epidemic, July–October 1916, it is shown that the maximum concentration of activity of poliomyelitis occurred within a 128-km radius of New York City. Although the integrity of the poliomyelitis cluster was maintained up to approximately 500 km from the metropolitan focus, the level and rate of propagation of disease declined with distance from the origin of the epidemic. Finally, it is shown that the geographical transmission of the epidemic in north-eastern USA probably followed a process of mixed contagious–hierarchical diffusion.
Keywords: Diffusion, Emergent diseases, Geography, Poliomyelitis, Spatial association analysis, USA
1. Introduction
The great epidemic of poliomyelitis that swept north-eastern USA in 1916 ranks as one of the largest and most intense outbreaks of the disease that has ever been recorded globally. In the words of Surgeon Claude H. Lavinder, in his capacity as Medical Director of the US Public Health Service, the epidemic marked ‘an epoch in the history of infantile paralysis’ (Lavinder et al. (1918), page 8), yielding around 23000 documented cases of clinical illness and leaving a larger geographical imprint than any previous outbreak of the disease. As a dramatic example of the emergence of an epidemic of a once rare and sporadic malady, the events of 1916 eclipsed all earlier outbreaks of the disease and heralded the recognition of poliomyelitis as a significant public health problem in the USA (Emerson, 1917; Lavinder et al., 1918).
As a reference point for the historical emergence of poliomyelitis, the US epidemic of 1916 has been revisited by epidemiologists, historians of medicine and others on numerous occasions and from a variety of perspectives (Paul et al., 1932; Galishoff, 1976; Nathanson and Martin, 1979; Rogers, 1989; Risse, 1992). However, relatively little is known of the geographical patterns and processes by which poliomyelitis spread to epidemic maturity during the summer of 1916. Consequently, we present here a geographical investigation of the epidemic, drawing on the data that were collected under the auspices of the US Public Health Service and published in the seminal report of Lavinder et al. (1918). In so doing, we re-examine the disease data that were presented by Lavinder and colleagues in the light of recent advances in the spatial analysis of infectious diseases (Cliff and Haggett, 1988a; Cliff et al., 1998a).
The paper begins in Section 2 by providing an epidemiological context for the study. In Section 3, we outline the nature of the poliomyelitis data that were gathered by the US Public Health Service, and we describe how the original counts of poliomyelitis were used to form geocoded databases of activity of the disease for sample states of north-eastern USA. In subsequent sections (Sections 4–6) a series of methods are used to decipher the patterns and processes by which poliomyelitis spread within north-eastern USA during the main period of epidemic activity, July–October 1916.
The empirical work will show that, although the epidemic of 1916 spread across much of north-eastern USA, the main focus of activity of the disease occurred within a 128-km radius of the putative origin of the outbreak (Brooklyn, New York City). At greater distances, the level of spatial concentration fell away such that, beyond 500 km, dissipation of the epidemic wave had resulted in a collapse of the New York cluster. Further exploratory analyses suggest that the spatial diffusion of the epidemic is consistent with a process of mixed contagious–hierarchical transmission, and that the rate of propagation of the epidemic declined with distance from the metropolitan epicentre.
2. Background to the epidemic of 1916
2.1. The nature of poliomyelitis
Poliomyelitis is an acute viral disease which is produced by three antigenically distinct types of poliovirus (types 1–3). The disease is spread through close contact and is primarily transmitted via the faecal–oral route. Infection is overwhelmingly subclinical, with the estimated ratio of inapparent to severe (paralytic) infections ranging up to 850:1. Clinically, poliomyelitis occurs in three main types: abortive, non-paralytic and paralytic. Abortive poliomyelitis takes the form of a minor illness from 3–6 days after infection and is characterized by a range of non-specific symptoms including headache, sore throat, fever and vomiting. Non-paralytic poliomyelitis occurs as a major illness from 9–17 days after infection. Symptoms of the major illness include those of the minor illness (though, typically, in a more severe form), along with stiffness of the neck, back and legs. Hyperesthesia (undue sensitivity to stimuli which are felt as painful even though innocuous) and paresthesia (tingling) may also be observed. Finally, in paralytic poliomyelitis, paralysis (commonly of the lower limbs but potentially of all major muscle groups) occurs from the first to the 10th day of the major illness. As regards the prognosis for paralytic cases, muscle power may return over a period of about 18 months following termination of the disease, after which time residual paralysis is usually permanent. Mortality from poliomyelitis is primarily due to suffocation arising from paralysis of the respiratory muscles, although other complications may also result in a fatal outcome. The case fatality rate is of the order of 5–10% (Krugman et al., 1977; Christie, 1987; Melnick, 1997; Mandell et al., 2000).
2.2. Historical context: the epidemic of 1916 in long-term perspective
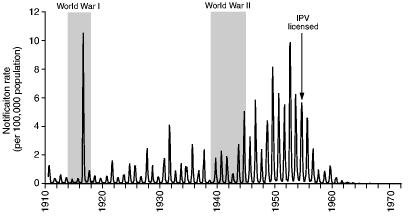
At the time, the 1916 epidemic of poliomyelitis in north-eastern USA formed the largest epidemic of the disease that had ever been reported—in North America, or elsewhere (Trevelyan et al., 2005). According to Lavinder et al. (1918), page 209, biographers and contemporary investigators of the epidemic, it marked the culmination of ‘a recent and rapid development of epidemic prevalence’, yielding around 23000 cases and 5000 deaths. To place the epidemic in long-term perspective, Fig. 1 is based on the federal disease returns of the USA and plots the national notification rate for poliomyelitis (per 100000 population) for a six-decade period from the start of formal surveillance in 1910. With the exception of the towering anomaly of 1916, Fig. 1 shows that the early decades of the 20th century were characterized by periodic epidemics of modest proportions. From the late 1930s, however, epidemics began to grow in magnitude, reaching a peak in the decade after World War II. Thereafter, the development and mass administration of inactivated and live poliovirus vaccines served as an effective curb on the activity of the disease so that, by the 1970s, the circulation of wild poliovirus had virtually ceased in the USA (Paul, 1971).
Fig. 1.
Monthly rate of notifications of poliomyelitis (per 100 000 population) in the USA, July 1910–December 1971: the date of introduction of inactivated poliovirus vaccine (IPV) is indicated (source: series constructed from state level notifications included in the Public Health Reports (Washington DC: Government Printing Office, 1910–1951) and Morbidity and Mortality Weekly Report (Atlanta: Centers for Disease Control, 1952–1972))
3. The data
3.1. Statistical data sources
The 1916 epidemic of poliomyelitis first attracted the attention of local public health officers on Thursday, June 8th. On this day, four cases of frank disease were reported in the borough of Brooklyn, New York City. Alerted to the possibility of a more extensive outbreak of unrecorded disease, preliminary investigations revealed many further cases of poliomyelitis—in both Brooklyn and Manhattan—so that, on Saturday, June 17th, epidemic conditions were publicly declared in New York City (Lavinder et al. (1918), pages 92–93). Shortly thereafter, Surgeon Claude H. Lavinder was charged with the responsibility of supervising the epidemiological and statistical investigation of the epidemic. From a central office in New York City, Lavinder, in association with his colleagues Allen W. Freeman, Wade Hampton Frost and a field team of experienced service officers, examined daily and weekly reports of poliomyelitis in New York City and proximal states of north-eastern USA. 2 years after the initial onset of the epidemic, Lavinder, Freeman and Frost's seminal report on the 1916 poliomyelitis epidemic was finally published as Public Health Bulletin 91 (Lavinder et al., 1918).
Since its publication, the Lavinder–Freeman–Frost report has acquired considerable standing, both as a source of data on the early epidemiology of poliomyelitis (Paul, 1971) and as a reference point for those who are concerned with unravelling the epidemic transition of the disease (Nathanson and Martin, 1979). Alongside a textual exposition of the epidemic, one important feature of the report was its 74-page statistical appendix which included weekly counts of notifications of poliomyelitis in each of two sets of geographical divisions:
the five boroughs of New York City (Bronx, Brooklyn, Queens, Manhattan and Richmond) and
the 143 constituent counties of nine north-eastern states (Maine, Massachusetts, Connecticut, Rhode Island, Vermont, New York State, New Jersey, Delaware and Maryland) and the District of Columbia.
The present paper uses the epidemiological information in (a) and (b) to examine the spatial structure of the 1916 epidemic in north-eastern USA.
3.2. The numerical database
We preface our discussion of the database with a comment on the temporal coverage of the poliomyelitis data that are available for analysis. Although the ultimate onset of the epidemic can be traced to the early days of May 1916 (see Section 4.1), Lavinder et al. (1918), pages 92–93, observed that systematic surveillance for poliomyelitis in the early focus of the epidemic (New York City) awaited the establishment of a regular card-based reporting system in mid-to-late June. Before this, case totals are believed to be somewhat incomplete. For the present analysis, therefore, we limit our consideration of the epidemic to an 18-week period of regular statistical recording, beginning with the week ending Saturday, July 1st (week 1), and terminating with the week ending Saturday, October 28th (week 18). This observation period encompasses the main phase of transmission of the epidemic and includes around 96% of the approximately 21000 tabulated cases of poliomyelitis in the study area, May–November 1916.
3.2.1. Database formation
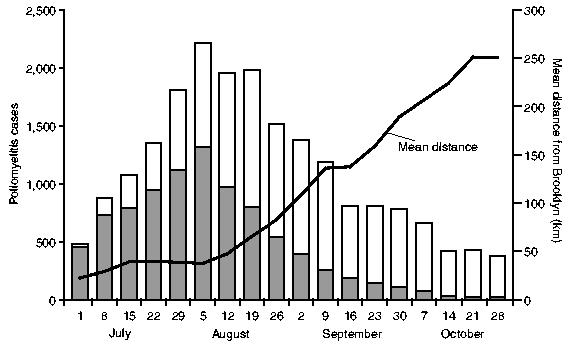
For the 18-week reporting interval, July–October 1916, counts of notifications of poliomyelitis in each of the five metropolitan boroughs (New York City) and 143 counties (nine north-eastern states and the District of Columbia) were abstracted from the statistical appendix of the Lavinder–Freeman–Frost report to yield a 148 (geographical unit) ×18 (week) space–time matrix of activity of disease. For convenience, the 148 geographical units (n) are referred to as ‘counties’ in the remainder of this paper. Table 1 gives the distribution of counties by major geographical division, along with summary details of the recorded epidemic of poliomyelitis. Finally, Fig. 2 plots the weekly count of notifications of poliomyelitis in the study area (histogram), along with the average distance of newly notified cases from the putative origin of the epidemic (Brooklyn, New York City) (line trace).
Table 1.
Notifications of poliomyelitis in the sample states and other geographical units of north-eastern USA, July–October 1916†
| State or area | Number of reporting counties (n) | Population ‡ | Notifications of poliomyelitis | Notification rate of poliomyelitis § |
|---|---|---|---|---|
| Connecticut | 8 | 1220486 | 805 | 85.4 |
| Delaware | 3 | 211599 | 72 | 34.0 |
| District of Columbia | 1 | 358679 | 42 | 11.7 |
| Massachusetts | 14 | 3953310 | 1673 | 21.6 |
| Maryland | 12 | 1054348 | 204 | 19.3 |
| Maine | 15 | 728620 | 115 | 15.8 |
| New Jersey | 21 | 2844344 | 4120 | 148.8 |
| New York City | 5 | 5040560 | 8884 | 176.3 |
| New York State | 53 | 4205991 | 3893 | 92.6 |
| Rhode Island | 5 | 602764 | 214 | 35.5 |
| Vermont | 11 | 311901 | 55 | 17.6 |
| Total | 148 | 20532602 | 20077 | 97.3 |
Source: based on information in Lavinder et al. (1918), appendix, pages 215-274.
Population estimates (1915) from state and federal censuses.
Rate per 100000 population.
Fig. 2.
Poliomyelitis in north-eastern USA, July–October 1916: weekly count of notifications of poliomyelitis in New York City (■) and other localities (□), and mean distance from Brooklyn of newly notified cases of poliomyelitis plotted by week (——)
3.2.2. Issues of data quality
Concerns over the completeness of morbidity statistics are a familiar problem in the epidemiological analysis of poliomyelitis (Lavinder et al., 1918; Nelson and Aycock, 1944; Serfling and Sherman, 1953; Trevelyan et al., 2005). As noted in Section 2.1, the clinical manifestations of poliovirus infection range from mild and non-specific symptoms to life-threatening paralysis. Under such circumstances, interarea comparisons of notifications of poliomyelitis are limited by geographical variations in both
the completeness of the reporting of severe (paralytic) disease and
the extent to which cases of less severe (non-paralytic) disease are included alongside paralytic disease in the case totals (Dauer, 1946).
The problems are especially acute when, as in the US epidemic of 1916, data are based on the non-uniform surveillance activities of a variety of city and state health departments, at least one of which (the state of Pennsylvania) was unwilling or unable to co-operate with the federal investigation. Although the latter factor has necessitated the exclusion of Pennsylvania from our analysis, we note from information that was included in the US Public Health Service's Public Health Reports (Washington DC, 1916) that, between May and November 1916, over 2000 cases of poliomyelitis were recorded in Pennsylvania. However, in the absence of spatially disaggregated data for the state, we limit our analysis and its interpretation to the original 148-county study area of Lavinder et al. (1918).
4. Spatial patterns of prevalence of poliomyelitis
The early months of 1916 gave no hint of the epidemic that was about to ensue. In New York City, a total of 13 cases of poliomyelitis had been recorded in the first 4 months of the year, which was a lower case total than for any equivalent period since the start of routine surveillance in 1910. A similar situation prevailed in the other cities of north-eastern USA, with the entire territory yielding just a handful of notifications each week (Lavinder et al. (1918), pages 87 and 162).
4.1. Origins of the epidemic
The apparent origin of the 1916 epidemic in north-eastern USA can be traced to Monday, May 8th. On this day, a case of poliomyelitis presented in the vicinity of Second Street and Fifth Avenue, a mixed industrial–residential area in the north-western sector of the borough of Brooklyn, New York City. The next day, a second case—‘some distance away’ from the first—presented in the south of the borough (Lavinder et al. (1918), page 87). With an initial focus on activity of the disease in the Italian community, additional cases of poliomyelitis were recorded in Brooklyn from May 15th, with the disease appearing soon thereafter in the boroughs of Queens (May 20th), Manhattan (May 25th) and Richmond (May 30th) (Lavinder et al. (1918), page 217). By June, poliomyelitis had begun to spread beyond the limits of New York City, first appearing in Hudson, New York, and Westfield, Massachusetts, and, soon thereafter, in other localities. By August, epidemic conditions prevailed throughout much of north-eastern USA.
4.2. Disease patterns
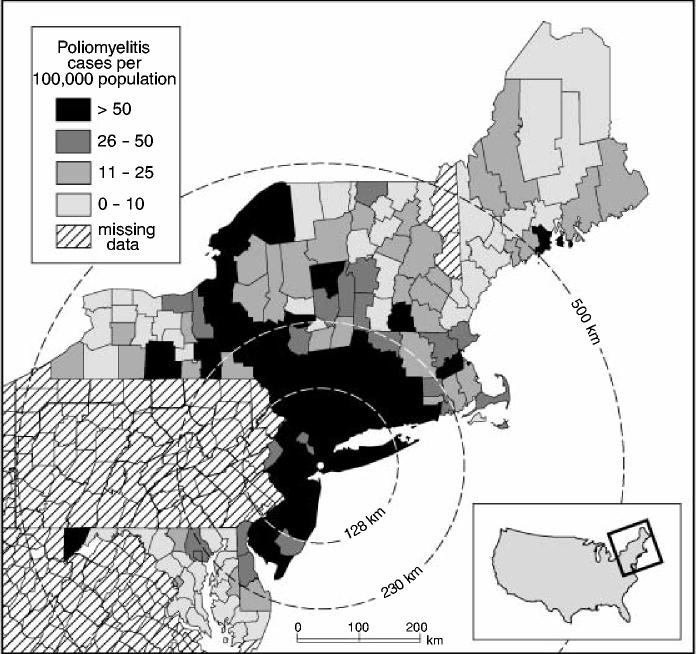
According to Lavinder et al. (1918), page 166, one of the most conspicuous features of the 1916 epidemic was the wavelike progression of the disease from New York City, with the level of activity of poliomyelitis declining with distance from the metropolitan focus of the outbreak. To provide an impression of this, Fig. 3 relates to the 148 sample counties in Table 1 and maps the notification rate for poliomyelitis (per 100000 population), July–October 1916. In the present section, we examine the nature of the pattern of disease that is illustrated in Fig. 3. We first use segmented regression analysis to test for evidence of a declining trend in the incidence of poliomyelitis with distance from New York City (Section 4.3). We then use techniques of spatial association analysis to assess the level of disease clustering around the metropolitan epicentre (Section 4.4).
Fig. 3.
Notification rates of poliomyelitis (per 100 000 population) by county for sample states of north-eastern USA, 1916: annuli, set at 128 km, 230 km and 500 km from Brooklyn, are plotted for reference; the annulus at 230 km is based on Fig. 4 and marks the break point in a segmented regression analysis of county level notification rates of poliomyelitis against distance from New York City; the annuli at 128 km and 500 km are based on the spatial association analysis in Fig. 5 and delimit the area within which the maximum spatial concentration of high rates of poliomyelitis occurred (128 km) and the maximum limit of the spatial cluster of poliomyelitis around New York City (500 km) (note that the state of Pennsylvania has been omitted from the analysis on account of missing information; source, drawn from information in Lavinder et al. (1918), Tables U–DD, pages 243–251, and map BB, opposite page 287)
4.3. Spatial trends in the incidence of poliomyelitis: segmented regression analysis
Fig. 4 is based on the information in Fig. 3 and plots, on the vertical axis, the natural logarithm of the notification rate for poliomyelitis (per 100000 population) for each of the 148 sample counties against, on the horizontal axis, the straight line distance (in kilometres) of county centroids from the documented geographical origin of the epidemic (Brooklyn, New York City). Here, the logarithmic transformation serves to linearize the relationship between rates of poliomyelitis and distance while, as indicated on the vertical axis of Fig. 4, the addition of 1 avoids the computational problem of zero values in the transformation.
Fig. 4.
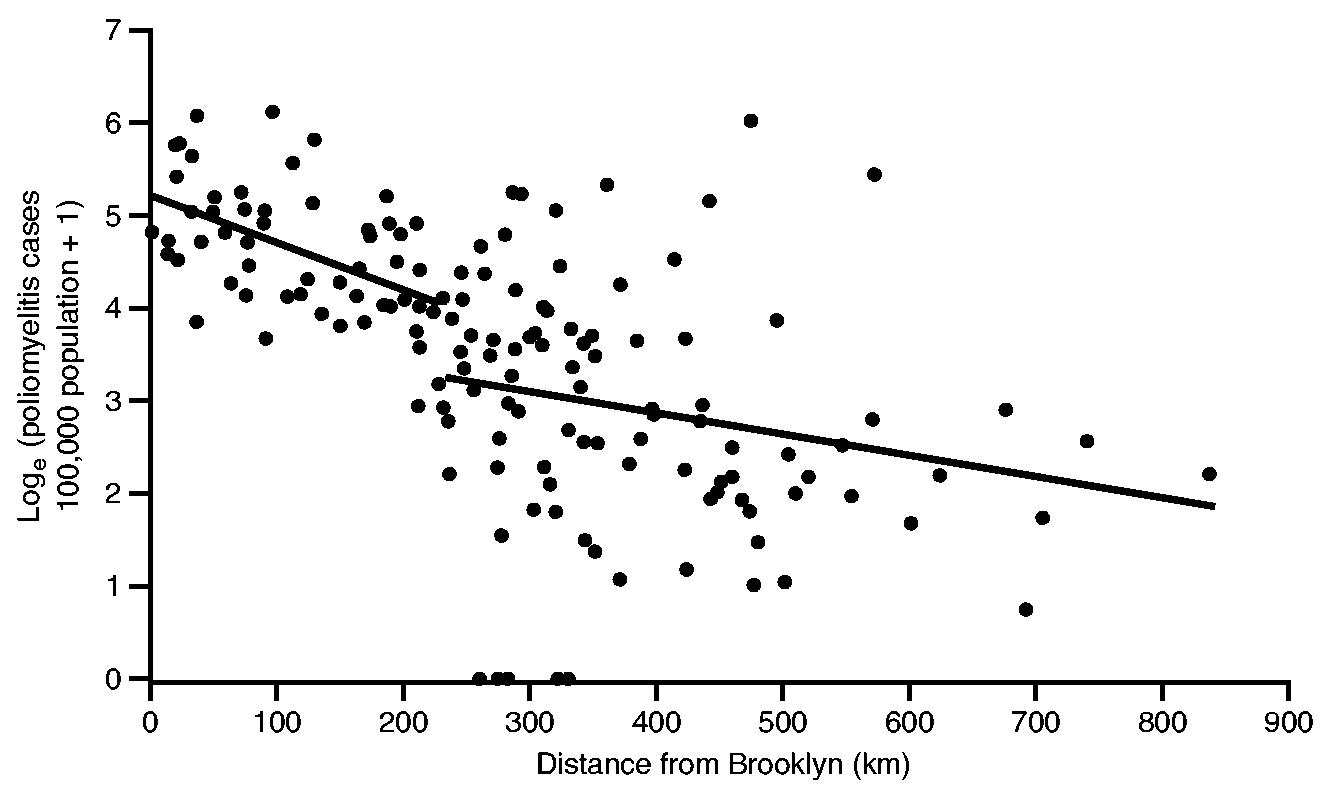
Poliomyelitis case rate (per 100 000 population) against distance from Brooklyn for 148 counties of north-eastern USA, July–October 1916: a segmented ordinary least squares regression model (with two straight line segments), defined in equation (1), was fitted at each possible division of the 148 data points;——, division which minimized the residual sum of squares
An inspection of the graph reveals a broad grouping of high rates of poliomyelitis near New York City, with evidence of a sharp shift to low rates at increasing distances from the metropolis. To capture the underpinning trend, a two-line segmented regression model of the form
| (1) |
was postulated (Draper and Smith, 1998). Here, ci is the notification rate for poliomyelitis (per 100000 population) in county i, x1 and x2 are distance variables that represent the position of data points on segments 1 and 2 of the regression model and x3 is a binary variable coded 1 (data points on segment 1) or 0 (data points on segment 2). Finally, β0 (the intercept coefficient of segment 1), β1 (the slope coefficient of segment 1), β2 (the slope coefficient of segment 2) and β3 (the vertical distance between segments 1 and 2) are parameters to be estimated. A disjoint model was selected to accommodate a step function change in the transformed values of ci at the division of segments 1 and 2.
Equation (1) was fitted to the data in Fig. 4 by ordinary least squares. Model fitting was undertaken by treating each of the 146 interpoint divisions of the scatter distribution as the possible break point; values of the variables x1, x2 and x3 were recomputed at each division, with all distances measured in kilometres. Following Draper and Smith (1998), page 317, the model that minimized the residual sum of squares was selected as the best fit solution.
4.3.1. Results
The results of the model fitting are summarized in Table 2, and the associated two-segment trend line is plotted in Fig. 4. As Fig. 4 indicates, the division in the segmented model occurs at a distance of 230 km from New York City. The break point marks a transition in the underlying downward trend in activity of poliomyelitis, from
a relatively steep reduction in rates of the disease as the epidemic wave advanced up to 230 km from New York City to
a relatively gentle reduction in rates of the disease beyond the 230-km point.
For reference, the transition point is demarcated by the 230-km annulus in Fig. 3.
Table 2.
Results of segmented regression analysis to examine the decline of the natural logarithm of poliomyelitis notification rates (per 100000 population) with distance from New York City, July–October 1916
| Estimated β coefficients (t-statistic) |
R2 (F-ratio) | |||
|---|---|---|---|---|
| 5.21 | −0.01 | −0.002 | −0.83 | 0.41 |
| (18.15†) | −(2.47‡) | −(2.47‡) | −(2.51‡) | (33.18†) |
Significant at the p=0.01 level (two-tailed test).
Significant at the p=0.05 level (two-tailed test).
Following Cliff and Ord (1981), pages 197–230, the residuals from the regression model in Table 2 were examined for evidence of spatial autocorrelation by using Moran's I -statistic. Details of the statistic are given in Section 6.3 but, using a nearest neighbour connection matrix to represent spatial proximity, the analysis yielded a standard normal score of 0.25. The result is non-significant at conventional levels of statistical inference and confirms the absence of spatial autocorrelation in the residuals from the segmented regression.
4.4. Geographical clustering of poliomyelitis: spatial association analysis
An alternative approach to the examination of the spatial disease pattern in Fig. 3 is to assess the level of clustering of poliomyelitis around New York City. For this, we draw on a measure of local spatial association which is known as the Gi(d) statistic (Getis and Ord, 1992; Ord and Getis, 1995). The Gi(d) statistic provides a measure of the spatial concentration of a given variable x (in the present analysis, the level of activity of poliomyelitis) within distance d of a specified reference point i. High values of Gi(d) are generated when large values of x cluster within distance d of reference point i, whereas low values of Gi(d) are generated when the converse is true. Following Getis and Ord (1992), page 190, Gi(d) is defined as
| (2) |
where n is the number of sample counties, d is the straight line distance (in kilometres) between the geographical centroids of Brooklyn i and county j, xj is the notification rate of poliomyelitis (per 100000 population) in j and {wij} is a symmetric binary spatial weights matrix in which wij = 1 if county j is within distance d of Brooklyn and wij = 0 otherwise. For large values of n, Gi(d) may be tested for significance as a standard normal deviate. Formulae for the computation of the expectation and variance under the null hypothesis of no spatial association are given in Getis and Ord (1992), page 192.
The specification of equation (2), with local indicator i fixed to the epidemic index location of Brooklyn, corresponds to the approach that was adopted by Ord and Getis (1995), pages 299–305, and permits an examination of the variation in Gi(d) with distance from the putative point of the onset of the epidemic. For the present analysis, Gi(d) was evaluated for each of the 147 increments of distance d associated with the centroids of counties j. The analysis was undertaken for
values of xj aggregated over the 18-week observation interval (Section 4.4.1) and
values of xj disaggregated for each week of the 18-week observation interval (Section 4.4.2).
4.4.1. Results, I: temporally aggregated analysis
Fig. 5 is based on the aggregated rates of poliomyelitis for the 18-week observation period and plots, as black circles, the values of the Gi(d) statistic as a standard normal deviate for each of the 147 centroid-based distance bands from Brooklyn. The broken horizontal line at z = 1.65 marks the nominal p = 0.05 level for Gi(d) in a one-tailed test for positive spatial association. This level should only be used as a guide because of potential correlation between values of Gi(d) at contiguous distances from Brooklyn, caused by spatial autocorrelation between the {xj} in equation (2). The distribution theory of Gi(d) under these circumstances is not accurately known. But, despite this caveat, it remains that, the larger (positive) the values of z become, the greater is the degree of clustering of high rates of poliomyelitis within distance d of Brooklyn. Finally, the grey circles in Fig. 5 plot the corresponding rates of poliomyelitis (per 100000 population) for the sample counties.
Fig. 5.
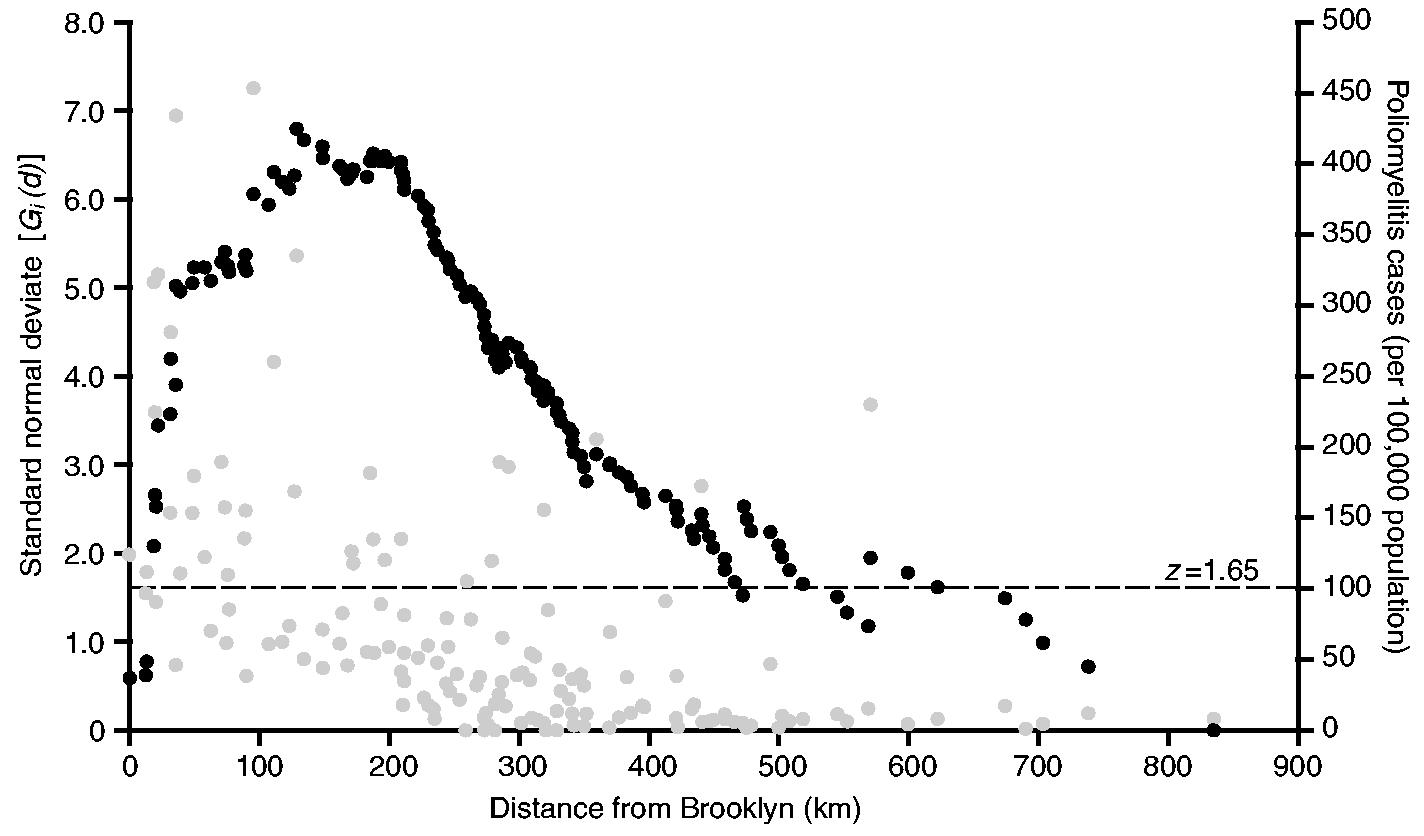
Spatial association of activity of poliomyelitis in north-eastern USA, July–October 1916: •, value of the Gi(d) statistic, as a standard normal deviate, for a series of distances from Brooklyn (distances are defined by the positions of 148 counties of north-eastern USA); •, poliomyelitis case rate (per 100000 population) for counties against their distance from Brooklyn; – – –, z = 1.65 line, marking the nominal significance of Gi(d) at the p = 0.05 level in a one-tailed test for the spatial association of high values
With the exception of very short (less than 10 km) and very long (greater than 500 km) distances, the overwhelming majority of values of Gi(d) in Fig. 5 are 1.65 or greater, indicating that the rates of poliomyelitis were markedly spatially similar up to 500 km around New York City. Within this area, which is demarcated by the annulus at 500 km in Fig. 3, two further features of Fig. 5 are also noteworthy.
The highest value of Gi(d) is recorded at 128 km and delimits the area within which the maximum spatial concentration of high rates of poliomyelitis occurred. Again, the area is demarcated in Fig. 3. For the 31 reporting counties within the 128-km radius, the average rate of poliomyelitis was 171 per 100000 population; for the remaining counties, located beyond the 128-km radius, the average rate was just 40 per 100000 population.
Beyond 210 km, which approximates the transition point in the segmented regression analysis (Fig. 4), the series of Gi(d) is characterized by a long tail of falling values. Although a significant concentration of high rates of poliomyelitis is maintained up to 500 km from New York City, the strength of the cluster weakens with increasing distance from the 210-km transition point.
4.4.2. Results, II: temporally disaggregated analysis
To examine the evolution of the poliomyelitis cluster in Fig. 5, the contour plot in Fig. 6 charts the weekly values of Gi(d) as a standard normal deviate (vertical axis) by rank of distance from Brooklyn (horizontal axis). In forming the horizontal axis, rank order has been plotted on the basis of equal spacing; absolute distances (in kilometres) associated with sample counties are indicated for reference. Consistent with Fig. 5, the peak value of Gi(d) is at a distance of 128 km in the week ending August 12th (week 7). Overall, the surface is characterized by high values at intermediate distances from New York City, with low values at distances that are both close to and far from the metropolis. When read in terms of both the strength (vertical axis) and the distance (horizontal axis) components of Fig. 6, the analysis suggests a simple four-stage model of the temporal progression of the epidemic:
June 25th–July 22nd (weeks 1–4)—poliomyelitis activity was tightly focused around New York City, with the highest concentration of the disease cluster within 30–40 km of the metropolis, and with the significance of the cluster falling at greater distances;
July 26th–August 12th (weeks 5–7)—the limit of the disease cluster expanded outwards to 128 km, with a continued intensification of activity of poliomyelitis within this primary focus;
August 13th–September 23rd (weeks 8–13)—as the epidemic began to wane, the spatial concentration of poliomyelitis around New York City began to weaken, but with an expansion of the greatest clustering to a distance of 473 km from the metropolis (week 13);
September 24th–October 28th (weeks 14–18)—the spatial concentration of poliomyelitis around New York City collapsed from week 14, with no evidence of clustering about the city thereafter.
Fig. 6.
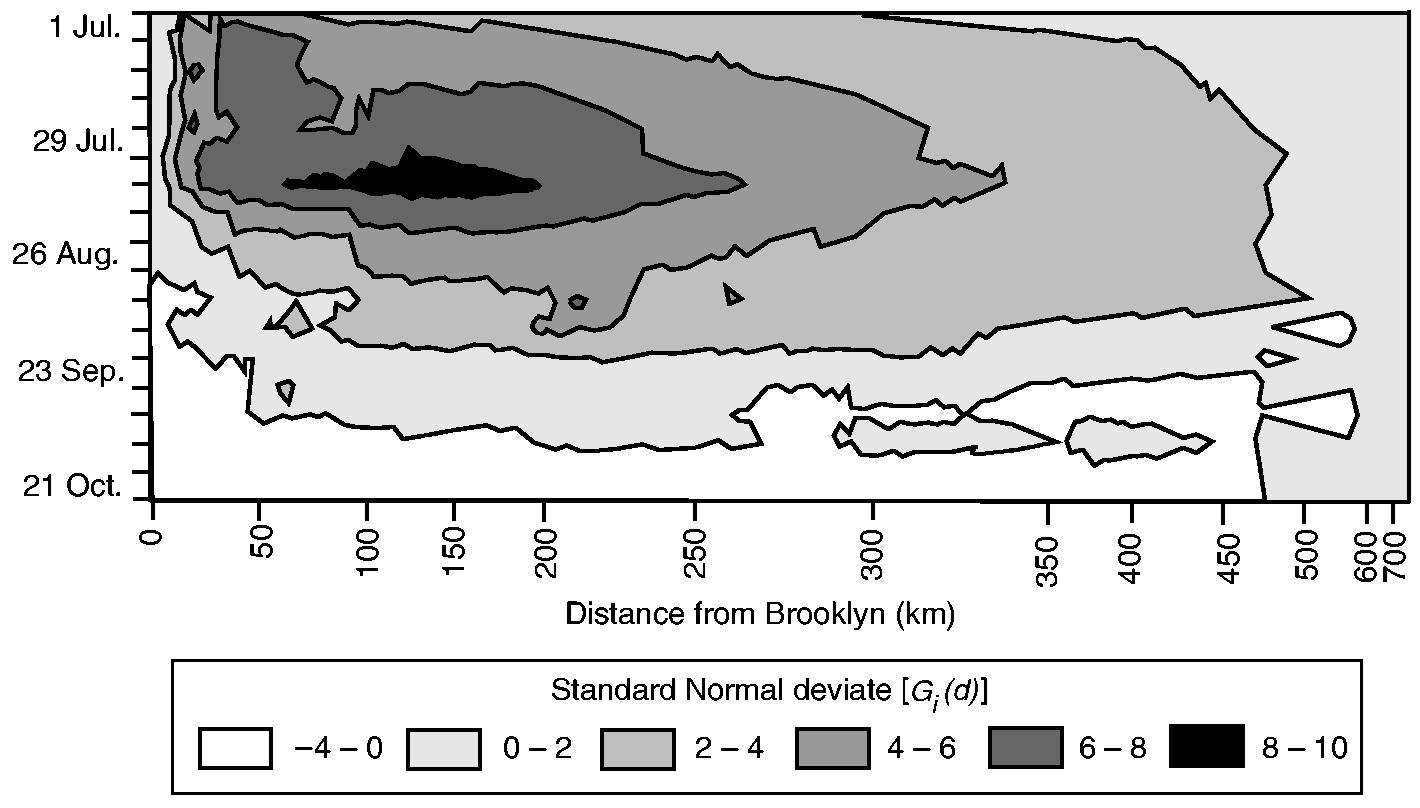
Contour plot of the value of the Gi(d) statistic, as a standard normal deviate, by week and by distance from Brooklyn: darker shading categories indicate greater values of Gi(d); the horizontal axis has been formed by ranking the 148 counties in terms of their straight line distance from Brooklyn; absolute distances (in kilometres) are given; beginning at the upper left-hand sector of the plot, values of the Gi(d) statistic display a tendency to reduce with spatial (horizontal axis) and temporal (vertical axis) distance from New York City
5. Velocity of the epidemic
A fundamental question that can be asked of the 1916 epidemic relates to the rate—or velocity—at which poliomyelitis spread within north-eastern USA. Did the epidemic differ in its rate of propagation in the counties under investigation? If so, how were these differences related to the spatial extension of the epidemic wave from New York City?
5.1. Measures of epidemic velocity
Statistical methods for the assessment of the velocity of an epidemic have been reviewed by Cliff et al. (1986) and Cliff and Haggett (1988b). For the present analysis, the velocity was assessed by using the higher order moments of the frequency distribution of notifications of poliomyelitis against time. Following Cliff et al. (1986), pages 199–200, denote the first week of the observation period as t = 1, with subsequent weeks coded serially as t = 2,3,…, T , where T is the number of weekly periods from the beginning to the end of the observation period. Then, the mean (average) time to infection, t̄, is defined as
| (3) |
where xt is the number of notifications of poliomyelitis in week t and n = Σ xt for all t. The rth central moment about t̄ may be written as
| (4) |
Using equation (4), we may then define two measures of epidemic velocity as
| (5) |
The quantities b1 and b2 are measures of skewness and kurtosis respectively. Further details are given in Cliff et al. (1986), pages 200–201, but, consistent with the classic studies of epidemic waveforms by Kendall (1957), relatively fast epidemic waves are characterized by a positive value for the coefficient of skewness b1, and a large value of the coefficient of kurtosis b2. Conversely, relatively slow epidemic waves are characterized by a negative value for b1 and a small value of b2.
The measures of epidemic velocity in equation (5) were evaluated for the set of 148 counties under observation. Excluding the counties for which no cases were recorded (five counties) or for which cases were recorded in only 1 week of the observation period (16 counties), the analysis was limited to a subsample of 127 geographical units.
5.2. Distance–velocity studies
Theoretical and empirical studies of the spatial transmission of infectious diseases have indicated a negative association between velocity and distance as an epidemic wave fans outwards from its geographical point of origin. Details are provided elsewhere (Cliff et al. (2000), pages 120–123) but, following the theoretical analyses of Kendall (1957), a distance-dependent reduction in the rate of epidemic propagation may be expected to arise from a change in the parameters controlling the size and mixing of susceptible populations. For a disease such as poliomyelitis, these changes may result from such factors as latent immunization arising from natural exposure to poliovirus and/or the timely implementation of methods of epidemic control as public health officers become alerted to the existence of an outbreak (see Cliff et al. (2000), page 123).
5.2.1. Method: regression analysis
To test for distance-related changes in the velocity of the 1916 poliomyelitis epidemic in north-eastern USA, the regression models
| (6) |
and
| (7) |
were postulated. Here, b1i and b2i are the Pearson measures of skewness and kurtosis for county i, di is the straight line distance (in kilometres) of i from Brooklyn and ei is a normal error term. Formed in this manner, the regression models in equations (6) and (7) were fitted by ordinary least squares to the set of n=127 counties for which estimates of b1 and b2 were available.
5.2.2. Results
Consistent with the expected reduction in velocity with increasing distance from New York City, statistically significant and negative trends were identified for both the skewness coefficient b1 and the kurtosis coefficient b2 < 0.001).
5.2.3. Discussion
Lavinder, Freeman and Frost were cognisant of the changing form of epidemic waves as polio-myelitis advanced from its metropolitan focus. ‘The mass movement of the epidemic’, Lavinder et al. (1918), page 204, observed, ‘shows … a definite wavelike movement, … diminishing in amplitude as it recedes from the central point.’ They failed, however, to connect such a change in waveform to underlying shifts in the rate of propagation of the epidemic. In the present section, we have drawn on statistical extensions of the classic waveform studies of Kendall (1957) to demonstrate how changes in two basic parameters of epidemic waves (skewness and kurtosis) signalled a progressive reduction in velocity with increasing distance from New York City. This finding parallels the reduction in prevalence of the disease that was identified in Section 4.3 and, following the theoretical work of Kendall, is consistent with a progressive fall in the susceptible and/or exposed population as the epidemic wave advanced towards the periphery of the study area (see, for example, Cliff and Haggett (1988a), pages 183–185, and Cliff et al. (2000), pages 120–123).
6. Epidemic diffusion processes
Although the foregoing analysis provides insights into the rate at which poliomyelitis diffused within north-eastern USA, alternative methods are required to determine the nature of the processes that underpinned the spread of the epidemic. In this section, we use complementary statistical techniques (regression analysis and spatial autocorrelation analysis) to identify the manner in which poliomyelitis diffused to the spatial pattern that is shown in Fig. 3.
6.1. Types of epidemic diffusion process
Our analysis begins with a brief comment on diffusion processes. As described more fully elsewhere (see, for example, Smallman-Raynor and Cliff (1998, 2001, 2002)), accounts of the geographical spread of an infectious disease usually recognize three main types of diffusion process:
a contagious process in which the disease moves wavelike from its centre of introduction to other centres—this process is formed to reflect the heightened population mixing that may occur between proximal centres;
a hierarchical process in which the disease moves progressively through the population hierarchy, typically from large to small centres—this process is formed to reflect the heightened population mixing that may occur between large centres, irrespective of their geographical proximity, because of their importance in providing goods and services;
a mixed process in which the spread pattern contains both contagious and hierarchical components.
These processes have all been used to underpin spatial models of the transmission of measles by Grenfell and colleagues (see, for example, Grenfell et al. (2001) and Xia et al. (2004)). In this paper, we examine the applicability of the contagious, hierarchical and mixed contagious–hierarchical diffusion models to the 1916 epidemic.
6.2. Spatial diffusion analyses, I: regression methods
6.2.1. Method
The application of regression techniques to the examination of epidemic diffusion processes was outlined by Cliff et al. (1981, 1986) and Smallman-Raynor and Cliff (1998, 2002). In the context of the present study, the time-ordered sequence of appearance of poliomyelitis in the counties of north-eastern USA was modelled as a function of
population size Pi, representing the hierarchical component in the spread processes, and
the straight line distance di in kilometres from the putative origin of the epidemic (Brooklyn, New York City), representing the contagious component.
The first week of the observation period (the week ending July 1st) was coded as week 1 and, for county i, the week in which poliomyelitis was first recorded was coded as week 2, or 3, or 4, etc. The typical week for county i was denoted as ti. Then the regression model
| (8) |
was postulated. A preliminary analysis revealed a double-logarithmic relationship between ti and Pi and a log-linear relationship between ti and di. The logarithmic transformations in equation (8) linearize these relationships, and ei is a normal error term.
The regression model in equation (8) was fitted to each of the 143 counties i for which non-zero poliomyelitis counts were recorded; the remaining five counties, each with a zero poliomyelitis count, were omitted from the analysis owing to the lack of a definable value of t. Model fitting was by ordinary least squares using a stepwise algorithm. One potential complication in the regression procedure is possible collinearity between population size and distance. In particular, a decrease in county population size with increasing distance would hinder separation of the contagious and hierarchical components in the model. Consequently, Pearson's r correlation coefficient was used to assess the level of correlation between the independent variables.
6.2.2. Results
The results are illustrated graphically in Fig. 7. A striking feature is the positive association between distance and time to infection (Fig. 7(a)) and the negative association between population size and time to infection (Fig. 7(b)). Generally, Fig. 7(a) implies that counties proximal to New York City were infected relatively early in the epidemic, with more distant counties infected at increasingly later dates. Similarly, Fig. 7(b) implies that the more populous counties were infected relatively early in the epidemic, with less populous counties infected at increasingly later dates. Together, the patterns in Figs 7(a) and 7(b) are consistent with the operation of a mixed contagious–hierarchical diffusion process.
Fig. 7.
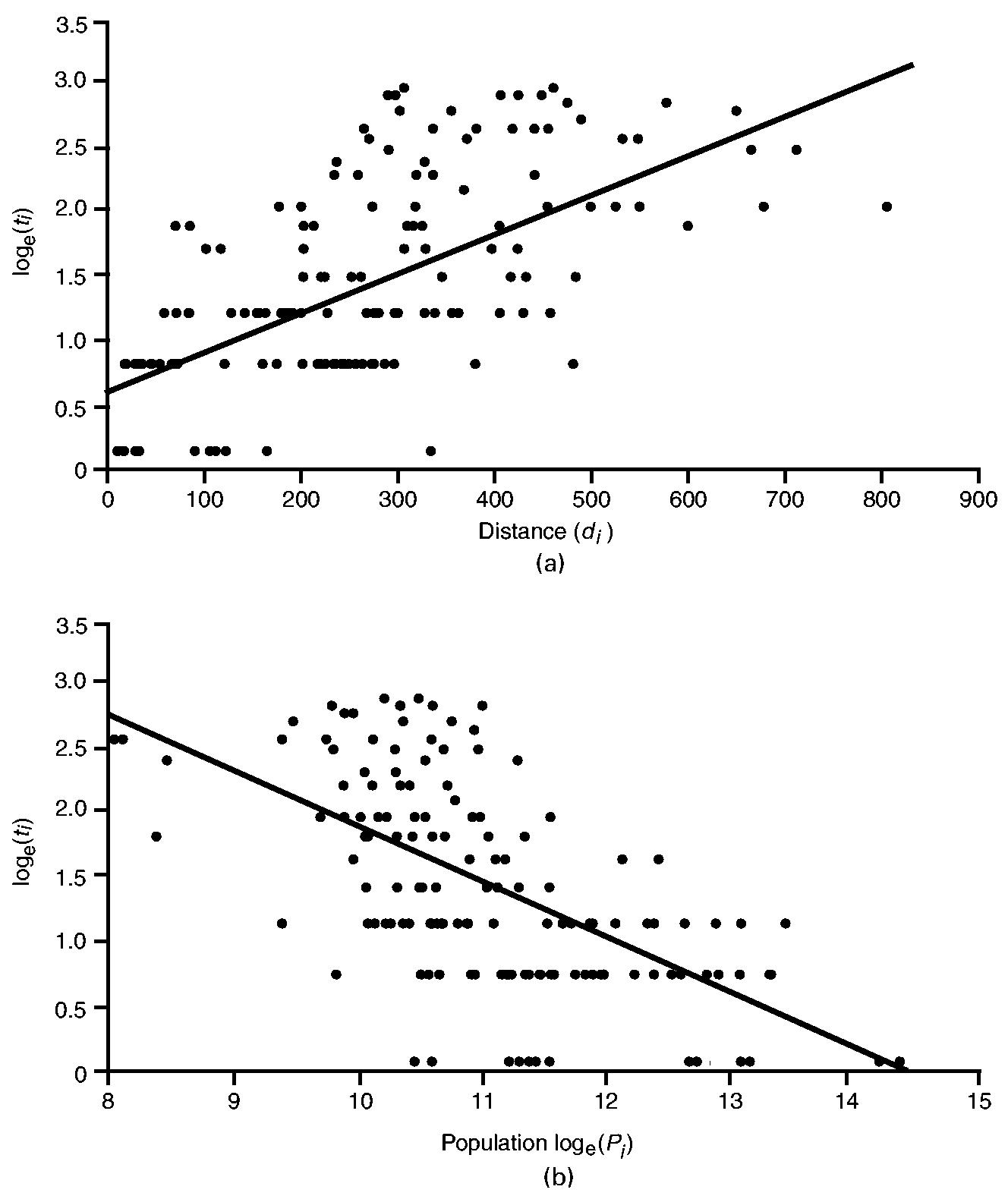
Diffusion of poliomyelitis in 148 counties of north-eastern USA, July–October 1916: (a) relationship between time to first appearance of poliomyelitis (ti) and distance to Brooklyn (di); (b) relationship between time to first appearance of poliomyelitis (ti) and population size (Pi) (note that ti and Pi have been logarithmically transformed; ———, linear trend lines fitted by ordinary least squares)
Table 3 examines the diffusion process by using the framework of the multiple-regression model that is defined in equation (8). Table 3 gives the order of entry (step) of the independent variables which results from the stepwise fitting procedure, along with the estimated slope coefficients and (with the associated t-statistics in parentheses), the coefficient of determination, R2, and the F -ratio. Finally, the degree of correlation, rloge(Pi)di, between the independent variables is also given. Statistically significant values at the p=0.01 level (two-tailed test) are indicated.
Table 3.
Results of stepwise multiple regression to identify the processes by which poliomyelitis diffused in the county system of north-eastern USA, July–October 1916†
| N | Intercept coefficient (t-statistic) | Independent variable, slope coefficient (t-statistic) |
R2 (F) | r loge(Pi)di | |
|---|---|---|---|---|---|
| Step 1 | Step 2 | ||||
| 143 | 4.13 (8.09‡) | di, 0.002 (8.01‡) | loge(Pi), −0.304 (−7.06‡) | 0.56 (88.75‡) | −0.36 |
Independent variables: di, the distance (in kilometres) of county i from Brooklyn and Pi, the estimated population of county i in 1915.
Significant at the p=0.01 level (two-tailed test).
Table 3 confirms that the time to infection is positively associated with the distance variable and negatively associated with the population variable, with the importance of local contagion underscored by the entry of the distance variable in step 1 of the model. When read in conjunction with Fig. 7, these results suggest that poliomyelitis spread through the counties of north-eastern USA as a mixed contagious–hierarchical diffusion process, with a dominant contagious component. We note, however, that the population gradient that is implied by the correlation between the two independent variables (rloge(Pi)di =–0.36) may have confounded the contagious and hierarchical in the modelling procedure.
6.3. Spatial diffusion analyses, II: autocorrelation on graphs
Although regression analysis provides an insight into the processes by which poliomyelitis first spread to each municipality in a given area, an alternative approach is required to determine the changing role of contagious and hierarchical components as the epidemic unfolded over time. One way to assess this temporal variability is by the application of spatial autocorrelation analysis. In the context of the foregoing regression analysis, the autocorrelation approach has an additional advantage: it allows us to isolate the potential confounding effects of the population gradient from the modelling procedure.
6.3.1. Method
The application of spatial autocorrelation analysis to epidemiological diffusion studies is described in Cliff et al. (1981), pages 99–102, and Cliff et al. (1986), pages 182–185. In brief, the area of the USA over which the spread is occurring is treated as a graph consisting of a set of nodes (in the present instance, 148 counties of north-eastern USA) and the links between them. These links can be formed to yield a graph that corresponds closely to a hypothetical diffusion process. Following Cliff et al. (1998b), pages 22–31, the study area was reduced to three graphs which represented the contagious, hierarchical and mixed diffusion processes that were outlined in Section 6.1:
contagious diffusion, nearest neighbour graph—this graph implies the localized spread of disease between proximal counties and was formed by setting each element wij in a matrix W equal to 1 if counties i and j were nearest neighbours as judged by the straight line distance between their geographical centroids, and wij = 0 otherwise;
hierarchical diffusion, hierarchical graph—this graph defines the area such that all counties are joined to their next largest and next smallest counties in terms of the rank order of county population sizes; it implies a strict hierarchical diffusion process, and was specified by setting wij = 1 if county j was the next larger or the next smaller county in population size to county i, and wij = 0 otherwise;
mixed diffusion, nearest larger neighbour graph—this graph, which incorporates elements of graphs (a) and (b), was formed by setting wij = 1 if county j was the geographically nearest of the counties that was larger in population size than county i, or if county j was the geographically nearest of the counties that was smaller in population size than county i; otherwise, wij = 0.
To determine the goodness of fit between each of the graphs and activity of poliomyelitis, the spatial autocorrelation coefficient, Moran's I , was computed for each week of the t = 18-element time series of poliomyelitis case rates (per 100000 population). Following Cliff and Ord (1981), pages 17–21, I is defined as
| (9) |
where n is the number of counties, xi is the poliomyelitis case rate per 100000 population in county i in a given week of the time series and zi = xi – x̄. The {wij} are drawn from graphs (a)–(c) above. In addition,
and we adopt the convention that wii = 0. I may be tested for significance as a standard normal deviate, and the expectation and variance under the null hypothesis of no spatial autocorrelation are given in Cliff and Ord (1981), page 21. Here, we note that, the greater the degree of correspondence between a given graph and the poliomyelitis case rate, the larger will be the value of the standard normal deviate that is associated with the I-coefficient. A fuller discussion of how to interpret I appears in Appendix A.
6.3.2. Results
Fig. 8 plots, as line traces, the weekly values of the spatial autocorrelation statistic, Moran's I, as a standard normal deviate for the contagious, hierarchical and mixed contagious–hierarchical diffusion graphs. The horizontal line set at z = 1:65 marks the nominal p = 0:05 level for I in a one-tailed test for positive spatial autocorrelation. Allowance was not made for multiple testing because the distribution theory for I under these circumstances is not known. Nevertheless, it remains the case that, the larger the value for z, the greater the degree of correspondence between a particular diffusion graph and the postulated diffusion process. For reference, the histogram in Fig. 8 plots the weekly rate of notifications of poliomyelitis (per 100000 population) for the study area. Taken relative to the peak week of activity of poliomyelitis (week 6, ending August 5th, 1916), weeks that are to the left of the epidemic peak (weeks 1–5) correspond to the build-up phase of the epidemic, whereas weeks that are to the right of the epidemic peak (weeks 7–18) correspond to the fade-out phase of the epidemic.
Fig. 8.
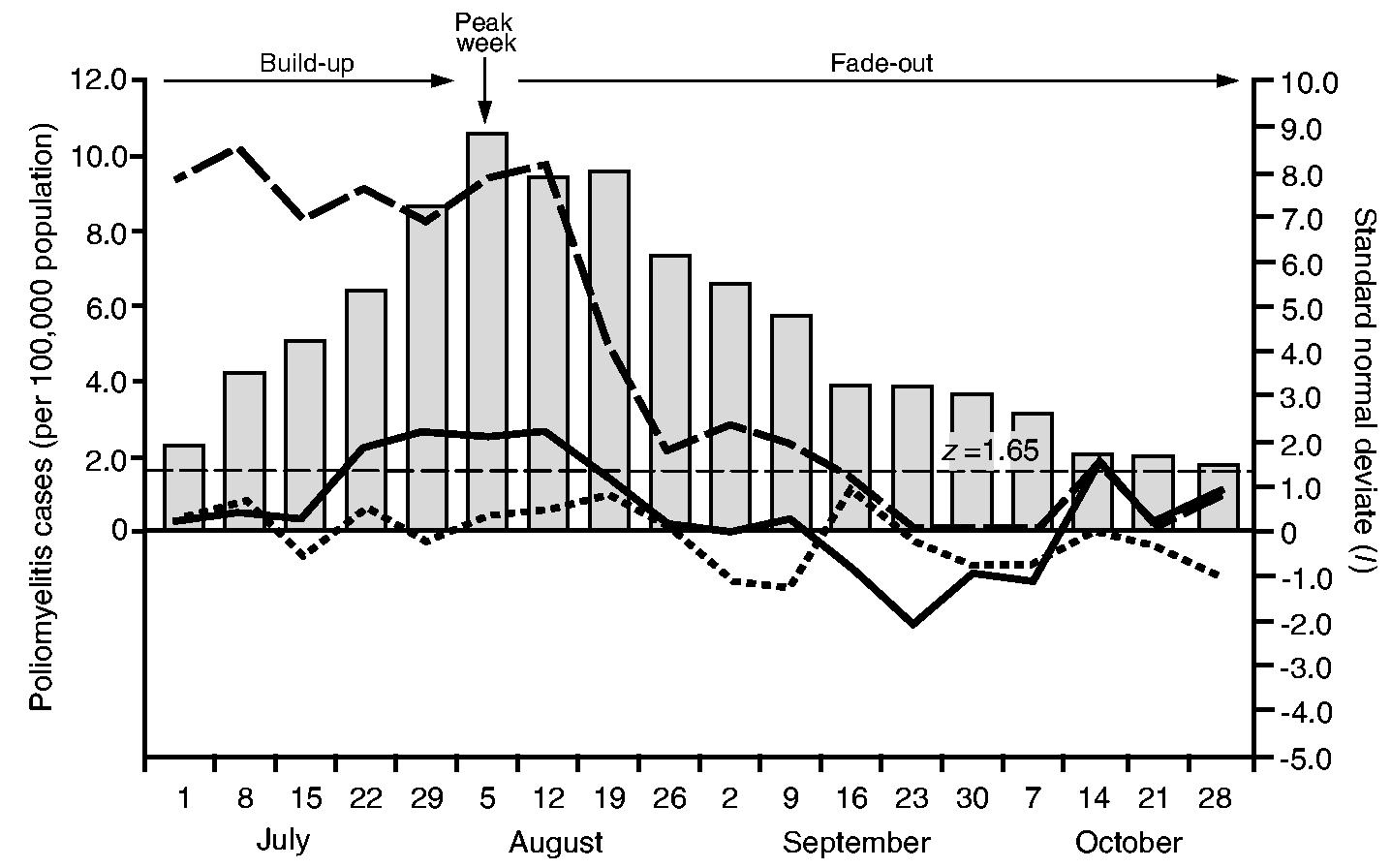
Processes of poliomyelitis diffusion in north-eastern USA, July–October 1916: the line traces plot weekly values of the spatial autocorrelation statistic, Moran's I, as a standard normal deviate for three hypothetical diffusion processes, contagious diffusion (——, nearest neighbour graph), mixed contagious–hierarchical diffusion (— —, nearest larger neighbour graph) and hierarchical diffusion (- - - - -, population hierarchy graph); ■, weekly notification rates of poliomyelitis (per 100000 population);——, z = 1.65 line, marking the nominal p = 0.5 level in a one-tailed test for positive spatial autocorrelation
Fig. 8 indicates that mixed contagious–hierarchical diffusion was important throughout the build-up and peak phases of the epidemic. From the second week of the fade-out period, however, the results imply that mixed transmission began to reduce in strength, falling to low levels from mid-September. In contrast, the operation of purely contagious diffusion was temporally concentrated around the late build-up, peak and early fade-out phases of the epidemic. Finally, the evidence in Fig. 8 suggests that purely hierarchical diffusion, in the strict form that is specified by graph (b) in Section 6.3.1, made no important contribution to the geographical spread of disease.
6.4. Interpretation
In a brief characterization of the spatial propagation of the 1916 epidemic, Lavinder et al. (1918), page 212, observed how
‘the extension was primarily to the larger centers of population and traffic in closest communication with New York, thence to the smaller urban and rural communities surrounding these secondary centers’.
Consistent with this model of transmission of the disease in the settlement system of north-eastern USA, the results of the county level studies in Sections 6.2 and 6.3 suggest that the spread of the epidemic conformed to a process of mixed contagious–hierarchical diffusion. Although this putative process was bolstered by purely contagious elements around the peak of the epidemic, the line traces in Fig. 8 imply that the underpinning mechanism of propagation of the epidemic had become detached from the structural parameters (population size and geographical proximity) of the county system by the latter stages of the observation period.
7. Conclusions
This paper has drawn on a classic disease data set, which was originally assembled by Lavinder et al. (1918), to re-examine the spatial parameters of one of the great historical examples of an emergent epidemic event: the outbreak of poliomyelitis that swept north-eastern USA in the summer of 1916. As Lavinder et al. (1918), page 10, explained of their data set,
‘Statistics of the disease [poliomyelitis] have never before been possible on such a large scale. Their collection and tabulation, even if they do not lead to immediate results of value, will undoubtedly prove of great importance to students of later epidemics. In the presentation of them we have tried to keep this point constantly in view.’
More than 85 years on, and with the advantage of modern computing capacity to hand, we have used a series of spatial quantitative techniques that were not available to the federal investigative team of 1916 to gain further insights into the epidemic. The particular methods that we have used form part of a large and diverse set of approaches that, under appropriate circumstances, may be employed in the spatial analysis of epidemiological data. The approaches have been reviewed by Lawson (2001) and Lawson and Denison (2002) and range from simple statistical descriptions of disease distributions to more advanced methods of spatial cluster modelling which we have not tackled here. Candidate modelling strategies include the susceptible–infectious–recovered models that were described in Xia et al. (2004) and the regression methodology of Diggle et al. (1997).
As described in Section 3.2.2, a failure of the state health authority of Pennsylvania to comply with the federal investigative team's request for county-specific poliomyelitis-related information has resulted in the omission of this state from the present analysis. Conditioned on this omission, three principal findings have emerged from our examination of the 1916 epidemic.
Although poliomyelitis was widespread in north-eastern USA during the summer and autumn of 1916, the main focus of activity of the disease remained localized around New York City and its hinterland. Although the statistical integrity of the disease cluster around New York City was maintained for distances of several hundred kilometres, the maximum spatial concentration of counties with high rates of poliomyelitis occurred within 128 km of the metropolitan focus. At greater distances, the level of spatial concentration fell away such that, beyond 500 km, dissipation of the epidemic wave had resulted in a statistical collapse of the radial disease cluster.
The rate of spatial propagation of the epidemic wave fell with increasing distance from New York City. This finding is consistent with an apparent dissipation of the energy of the epidemic wave that was observed in (a) and, following the theoretical work of Kendall (1957), may be accounted for by a progressive fall in the susceptible and/or exposed population as the epidemic wave advanced towards the periphery of the study area.
The spread of the epidemic in the county system of north-eastern USA appears consistent with a mixed process of localized spatial contagion and transmission down the population size hierarchy. Within the context of the diffusion models that were examined in the present paper, the evidence suggests that the build-up, peak and early fade-out phases of the epidemic were associated with the operation of a mixed contagious–hierarchical diffusion process. The later stages of the epidemic, however, were associated with a marked weakening of the process.
There is considerable scope for further research on the spatial structure of the 1916 epidemic of poliomyelitis in north-eastern USA. In the context of conclusion (a) above, for example, our analysis has been fixed relative to a single geographical unit—the putative origin and presumed main focus of the epidemic, Brooklyn. Possibilities for further exploratory analyses include the application of local indices of spatial association to alternative locations in the study area, or the use of a spatial scan statistic (Kulldorff, 1997) to screen for multiple local foci of activity of poliomyelitis (Smallman-Raynor et al., 2005). Similarly, in the context of conclusions (b) and (c), additional modelling approaches—of the type that is described in the present paper, but which seek to examine the lag structure of the epidemic sequence in space and time (Cliff and Haggett (1988a), pages 203–205)—would add much to our understanding of the evolution of the epidemic.
Acknowledgements
The work described has been undertaken as part of a 5-year programme of research entitled ‘Historical geography of emerging and re-emerging epidemics, 1850–2000’, funded by the Well-come Trust. The additional support of the Economic and Social Research Council (BT) and the Leverhulme Trust (MS-R) is also gratefully acknowledged. The authors thank the Joint Editor and the referees, whose helpful comments on an earlier version of this paper resulted in several substantial improvements in the analyses that are presented.
Appendix A: Interpretation of Moran's I
Moran's I has the classic form of a correlation coefficient (a ratio of covariance to variances of the variates). I measures the degree of similarity between the variate values of ‘close’ geographical units, where the degree of ‘closeness’ is determined by the non-zero weights, {wij}. The moments of I under the null hypothesis of no spatial autocorrelation may be evaluated by assuming that the observations are either
random independent drawings from one (or separate identical) normal population(s) or that they are
random independent drawings from one (or separate identical) population(s) with unknown distribution function(s), so that the set of all random permutations may be considered (randomization).
In this paper, we have used model (b). Under model (b), the expectation of I under the null hypothesis is
| (10) |
and
| (11) |
where, in addition to previous notation,
| (12) |
and
| (13) |
in which wi.= Σj wij and w.j = Σi wij. All summations are over n.
Because the expectation of I under the null hypothesis is not 0 and the range of values is both substantially less than 1 and varies by map structure as captured through the {wij}, it is easier to compare values by plotting I in standard score form. This has been done in Fig. 8. Cliff and Ord (1981), chapter 2, showed that, under random permutations, the sampling distribution of I under the null hypothesis is asymptotically normal as n increases and so the standard scores may be compared with normal score values to provide an approximate test of significance.
We refer to Moran's I in Section 6.3 as a coefficient of spatial autocorrelation, and so it is tempting to interpret the value of I as we would a correlation coefficient—i.e. restricted to the range [−1, 1] with values near ±1 indicating a very strong relationship. However, as described by Cliff and Ord (1981), pages 21–22, it may be shown by the Cauchy–Schwartz inequality that
| (14) |
where, developing the notation of Section 6.3.1, represents a value for zi that is suggested by the units with non-zero wij with i. In general, the upper bound for |I| will be less than 1, although it could exceed 1 for an irregular pattern of {wij} if units extreme values of zi are heavily weighted. When W (={wij}) is symmetric and n is large, the expected value of the upper bound under the null hypothesis is approximately
| (15) |
Thus, for a qualitative interpretation of I, a scaling by equation (14) can be helpful since it maps I onto a[−1, 1] interval like a conventional correlation coefficient. The drawback is that, in this form, the distribution theory becomes map specific rather than readily usable.
To interpret spatial autocorrelation coefficients more generally in the context of diffusion processes, high positive autocorrelation would imply close correspondence between the observed variate values and the diffusion graph postulated; high negative autocorrelation would imply heterogeneity between the variate values and the diffusion graph; values close to 0 would imply little association.
Finally, for applications of Moran's I to rate-based data, we note that variations in the population sizes of the geographical units under analysis may result in a loss of power of the test statistic (Assunção and Reis, 1999). All the results that were presented in Section 6.3 are subject to this potential limitation.
References
- Assunção RM, Reis EA. A new proposal to adjust Moran's I for population density. Statist. Med. 1999;18:2147–2162. doi: 10.1002/(sici)1097-0258(19990830)18:16<2147::aid-sim179>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- Christie AB. Infectious Diseases: Epidemiology and Clinical Practice. 4th edn. Vol. 2. Churchill Livingstone; Edinburgh: 1987. [Google Scholar]
- Cliff AD, Haggett P. Atlas of Disease Distributions: Analytic Approaches to Epidemiological Data. Blackwell; Oxford: 1988a. [Google Scholar]
- Cliff AD, Haggett P. Methods for the measurement of epidemic velocity from time-series data. Int. J. Epidem. 1988b;11:82–89. doi: 10.1093/ije/11.1.82. [DOI] [PubMed] [Google Scholar]
- Cliff AD, Haggett P, Ord JK. Spatial Aspects of Influenza Epidemics. Pion; London: 1986. [Google Scholar]
- Cliff AD, Haggett P, Ord JK, Versey GR. Spatial Diffusion: an Historical Geography of Epidemics in an Island Community. Cambridge University Press; Cambridge: 1981. [Google Scholar]
- Cliff AD, Haggett P, Smallman-Raynor M. Deciphering Global Epidemics: Analytical Approaches to the Disease Records of World Cities, 1888–1912. Cambridge University Press; Cambridge: 1998a. [Google Scholar]
- Cliff AD, Haggett P, Smallman-Raynor M. Detecting space–time patterns in geocoded disease data: cholera in London, 1854, and measles in the United States, 1962–95. In: Gierl L, Cliff AD, Valleron AJ, Farrington P, Bull M, editors. Geomed '97: Proc. Int. Wrkshp Geomedical Systems. Teubner; Leipzig: 1998b. pp. 13–42. [Google Scholar]
- Cliff AD, Haggett P, Smallman-Raynor M. Island Epidemics. Oxford University Press; Oxford: 2000. [Google Scholar]
- Cliff AD, Ord JK. Spatial Processes: Models and Applications. Pion; London: 1981. [Google Scholar]
- Dauer CC. Incidence of poliomyelitis in the United States in 1945. Publ. Hlth Rep. 1946;61:915–921. [PubMed] [Google Scholar]
- Diggle P, Morris S, Elliott P, Shaddick G. Regression modelling of disease risk in relation to point sources. J. R. Statist. Soc. A. 1997;160:491–505. [Google Scholar]
- Draper NR, Smith H. Applied Regression Analysis. 3rd Wiley; New York: 1998. [Google Scholar]
- Emerson H. A Monograph on the Epidemic of Poliomyelitis (Infantile Paralysis) in New York City in 1916: based on the Official Reports of the Bureaus of the Department of Health. Department of Health; New York City: 1917. [Google Scholar]
- Galishoff S. Newark and the great polio epidemic of 1916. New Jers. Hist. 1976;94:101–111. [PubMed] [Google Scholar]
- Getis A, Ord JK. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992;24:189–206. [Google Scholar]
- Grenfell BT, Bjørnstad ON, Kappey J. Travelling waves and spatial hierarchies in measles epidemics. Nature. 2001;414:716–723. doi: 10.1038/414716a. [DOI] [PubMed] [Google Scholar]
- Kendall DG. La propagation d'une épidémie au d'un bruit dans une population limitée. Publ. Inst. Statist. Univ. Paris. 1957;6:307–311. [Google Scholar]
- Krugman S, Ward R, Katz SL. Infectious Diseases of Children. Mosby; Saint Louis: 1977. [Google Scholar]
- Kulldorff M. A spatial scan statistic. Communs Statist. Theory Meth. 1997;26:1481–1496. [Google Scholar]
- Lavinder CH, Freeman AW, Frost WH. Public Health Bulletin 91. Government Printing Office; Washington DC: 1918. Epidemiologic studies of poliomyelitis in New York City and the northeastern United States during the year 1916. [Google Scholar]
- Lawson AB. Statistical Methods in Spatial Epidemiology. Wiley; Chichester: 2001. [Google Scholar]
- Lawson AB, Denison DGT, editors. Spatial Cluster Modelling. CRC Press; Boca Raton: 2002. [Google Scholar]
- Mandell GL, Bennett JE, Dolin R, editors. Principles and Practice of Infectious Diseases. 5th Churchill Livingstone; Philadelphia: 2000. [Google Scholar]
- Melnick JL. Poliovirus and other enteroviruses. In: Evans AS, Kaslow RA, editors. Viral Infections of Humans: Epidemiology and Control. 4th Vol. 21. Plenum; London: 1997. pp. 583–663. [Google Scholar]
- Nathanson N, Martin JR. The epidemiology of poliomyelitis: enigmas surrounding its appearance, epidemicity and disappearance. Am. J. Epidem. 1979;110:672–691. doi: 10.1093/oxfordjournals.aje.a112848. [DOI] [PubMed] [Google Scholar]
- Nelson NB, Aycock WL. A study of the reporting of paralytic poliomyelitis in Massachusetts, 1928–1941. Am. J. Hyg. 1944;40:163–169. [Google Scholar]
- Ord JK, Getis A. Local spatial autocorrelation statistics: distributional issues and an application. Geogr. Anal. 1995;27:286–306. [Google Scholar]
- Paul JR. The History of Poliomyelitis. Yale University Press; New Haven: 1971. [Google Scholar]
- Paul JR, Trask JD, Salinger R. Comparative statistical analyses of the 1916 and 1931 epidemics of poliomyelitis in and about the city of New Haven. Yale J. Biol. Med. 1932;5:39–54. [PMC free article] [PubMed] [Google Scholar]
- Risse GB. Revolt against quarantine: community responses to the 1916 polio epidemic, Oyster Bay, New York. Trans. Stud. Coll. Physicns Phildelph. 1992;14:23–50. [PubMed] [Google Scholar]
- Rogers N. Dirt, flies, and immigrants: explaining the epidemiology of poliomyelitis, 1900–1916. J. Hist. Med. Allied Sci. 1989;44:486–505. doi: 10.1093/jhmas/44.4.486. [DOI] [PubMed] [Google Scholar]
- Serfling RE, Sherman IL. Poliomyelitis distribution in the United States. Publ. Hlth Rep. 1953;68:453–466. [PMC free article] [PubMed] [Google Scholar]
- Smallman-Raynor M, Cliff AD. The Philippines insurrection and the 1902–4 cholera epidemic: part I—epidemiological diffusion processes in war. J. Hist. Geogr. 1998;24:69–89. [Google Scholar]
- Smallman-Raynor M, Cliff AD. Epidemic diffusion processes in a system of U.S. military camps: transfer diffusion and the spread of typhoid fever in the Spanish–American War, 1898. Ann. Ass. Am. Geogr. 2001;91:71–91. [Google Scholar]
- Smallman-Raynor M, Cliff AD. The geographical transmission of smallpox in the Franco–Prussian War: prisoner of war (POW) camps and their impact upon epidemic diffusion processes in the civil settlement system of Prussia, 1870–71. Med. Hist. 2002;46:241–264. [PMC free article] [PubMed] [Google Scholar]
- Smallman-Raynor M, Cliff AD, Haining RP, Trevelyan B. Detecting space–time clusters of infectious diseases: using a scan statistic to map the incidence of the 1916 poliomyelitis epidemic in the northeastern United States. 2005 [Google Scholar]
- Trevelyan B, Smallman-Raynor M, Cliff AD. The spatial dynamics of poliomyelitis in the USA: from epidemic emergence to vaccine-induced retreat, 1910–1971. Ann. Ass. Am. Geogr. 2005;95:269–293. doi: 10.1111/j.1467-8306.2005.00460.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia Y, Bjørnstad ON, Grenfell BT. Measles metapopulation dynamics: a gravity model for epidemiological coupling and dynamics. Am. Natur. 2004;164:267–281. doi: 10.1086/422341. [DOI] [PubMed] [Google Scholar]