Skip to main content
PMC home page
Taylor & Francis Open Select logoLink to Taylor & Francis Open Select
. 2011 Jun 8;46(3):399–424. doi: 10.1080/00273171.2011.568786

An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies

Peter C Austin 1,*
PMCID: PMC3144483  PMID: 21818162

Abstract

The propensity score is the probability of treatment assignment conditional on observed baseline characteristics. The propensity score allows one to design and analyze an observational (nonrandomized) study so that it mimics some of the particular characteristics of a randomized controlled trial. In particular, the propensity score is a balancing score: conditional on the propensity score, the distribution of observed baseline covariates will be similar between treated and untreated subjects. I describe 4 different propensity score methods: matching on the propensity score, stratification on the propensity score, inverse probability of treatment weighting using the propensity score, and covariate adjustment using the propensity score. I describe balance diagnostics for examining whether the propensity score model has been adequately specified. Furthermore, I discuss differences between regression-based methods and propensity score-based methods for the analysis of observational data. I describe different causal average treatment effects and their relationship with propensity score analyses.

Randomized controlled trials (RCTs) are considered the gold standard approach for estimating the effects of treatments, interventions, and exposures (hereafter referred to as treatments) on outcomes. Random treatment allocation ensures that treatment status will not be confounded with either measured or unmeasured baseline characteristics. Therefore, the effect of treatment on outcomes can be estimated by comparing outcomes directly between treated and untreated subjects (Greenland, Pearl, & Robins, 1999).

There is a growing interest in using observational (or nonrandomized) studies to estimate the effects of treatments on outcomes. In observational studies, treatment selection is often influenced by subject characteristics. As a result, baseline characteristics of treated subjects often differ systematically from those of untreated subjects. Therefore, one must account for systematic differences in baseline characteristics between treated and untreated subjects when estimating the effect of treatment on outcomes. Historically, applied researchers have relied on the use of regression adjustment to account for differences in measured baseline characteristics between treated and untreated subjects. Recently, there has been increasing interest in methods based on the propensity score to reduce or eliminate the effects of confounding when using observational data. Examples of recent use of these methods include assessing the effects of kindergarten retention on children's social-emotional development (Hong & Yu, 2008), the effectiveness of Alcoholics Anonymous (Ye & Kaskutas, 2009), the effects of small school size on mathematics achievement (Wyse, Keesler, & Schneider, 2008), and the effect of teenage alcohol use on education attainment (Staff, Patrick, Loken, & Maggs, 2008).

Our objective is to introduce the reader to the concept of the propensity score and to describe how methods based on it can be used to reduce or eliminate the effects of confounding when using observational data to estimate treatment effects. The article is divided into six sections as follows: first, I briefly describe the potential outcomes framework, causal treatment effects, RCTs, and observational studies. Second, I introduce the concept of the propensity score and describe four different methods in which it can be used to estimate treatment effects. Third, I describe methods to assess whether the propensity score model has been adequately specified. Fourth, I discuss variable selection for the propensity score model. Fifth, I compare the use of propensity score-based approaches with that of regression analyses in observational studies. Sixth, I summarize our discussion in the final section. A recently published tutorial and case study in this journal was written as a companion to this article to illustrate the application of propensity score methods to estimate the reduction in mortality due to provision of in-hospital smoking cessation counseling to current smokers who had been hospitalized with a heart attack (Austin, 2011a).

RANDOMIZED CONTROLLED TRIALS VERSUS OBSERVATIONAL STUDIES

Because propensity score methods allow one to mimic some of the characteristics of an RCT in the context of an observational study, I begin this article by describing a conceptual framework for RCTs. I first describe the potential outcomes framework, which has also been described as the Rubin Causal Model (Rubin, 1974). I conclude this section by defining what I mean by an observational study and highlighting the primary difference between an observational study and a randomized experiment.

The Potential Outcomes Framework and Average Treatment Effects

In the potential outcomes framework, there are two possible treatments (e.g., active treatment vs. control treatment) and an outcome. Given a sample of subjects and a treatment, each subject has a pair of potential outcomes: Yi(0) and Yi(1), the outcomes under the control treatment and the active treatment, respectively. However, each subject receives only one of the control treatment or the active treatment. Let Z be an indicator variable denoting the treatment received (Z = 0 for control treatment vs. Z = 1 for active treatment). Thus, only one outcome, Yi(Yi = Zi, Yi(l) + (1 − Zi)Yi(0)), is observed for each subject: the outcome under the actual treatment received.

For each subject, the effect of treatment is defined to be Yi(1) − Yi(0). The average treatment effect (ATE) is defined to be is E[Yi(1) − Yi(0)] (Imbens, 2004). The ATE is the average effect, at the population level, of moving an entire population from untreated to treated. A related measure of treatment effect is the average treatment effect for the treated (ATT; Imbens, 2004). The ATT is defined as E[Y(1)− 7(0)|Z = 1]. The ATT is the average effect of treatment on those subjects who ultimately received the treatment. In an RCT these two measures of treatment effects coincide because, due to randomization, the treated population will not, on average, differ systematically from the overall population.

Applied researchers should decide whether the ATE or the ATT is of greater utility or interest in their particular research context. In estimating the effectiveness of an intensive, structured smoking cessation program, the ATT may be of greater interest than the ATE. Due to potentially high barriers to participation and completion of the smoking cessation program, it may be unrealistic to estimate the effect of the program if it were applied to all current smokers. Instead, greater interest may lie in the effect of the program on those current smokers who elect to participate in the program. In contrast, when estimating the effect on smoking cessation of an information brochure given by family physicians to patients who are current smokers, the ATE may be of greater interest than the ATT. The cost and effort of distributing an information brochure is relatively low, and the barriers to a patient receiving the brochure are minimal.

Randomized Controlled Trials

In RCTs, treatment is assigned by randomization. As a consequence of randomization, an unbiased estimate of the ATE can be directly computed from the study data. An unbiased estimate of the ATE is E [Yi, (1) − Yi, (0)] = E [Y(1)] − E [Y(0)] (Lunceford & Davidian, 2004). The aforementioned definition allows one to define the ATE in terms of a difference in means (continuous outcomes) or a difference in proportions or absolute risk reduction (dichotomous outcomes). For dichotomous outcomes, alternative measures of effect include the relative risk and the odds ratio. When outcomes are dichotomous, the number needed treat (NNT), the reciprocal of the absolute risk reduction, denotes the number of subjects that one must treat to avoid the occurrence of one event.

Observational Studies

Cochran (1965) defined an observational study to be an empirical investigation in which the “objective is to elucidate cause-and-effect relationships… [in settings in which] it is not feasible to use controlled experimentation, in the sense of being able to impose the procedures or treatments whose effects it is desired to discover, or to assign subjects at random to different procedures” (p. 234). By this definition, an observational study has the same intent as a randomized experiment: to estimate a causal effect. However, an observational study differs from a randomized experiment in one design issue: the use of randomization to allocate units to treatment and control groups.

In observational studies, the treated subjects often differ systematically from untreated subjects. Thus, in general, I have that E[Y(1)|Z = 1] ≠ E [Y(1)] (and similarly for the control treatment). Thus, an unbiased estimate of the average treatment effect cannot be obtained by directly comparing outcomes between the two treatment groups. In subsequent sections, I describe how the propensity score can be used to estimate average treatment effects.

THE PROPENSITY SCORE AND PROPENSITY SCORE METHODS

The propensity score was defined by Rosenbaum and Rubin (1983a) to be the probability of treatment assignment conditional on observed baseline covariates: ei = Pr(Zi = 1|Xi). The propensity score is a balancing score: conditional on the propensity score, the distribution of measured baseline covariates is similar between treated and untreated subjects. Thus, in a set of subjects all of whom have the same propensity score, the distribution of observed baseline covariates will be the same between the treated and untreated subjects.

The propensity score exists in both randomized experiments and in observational studies. In randomized experiments the true propensity score is known and is defined by the study design. In observational studies, the true propensity score is not, in general, known. However, it can be estimated using the study data. In practice, the propensity score is most often estimated using a logistic regression model, in which treatment status is regressed on observed baseline characteristics. The estimated propensity score is the predicted probability of treatment derived from the fitted regression model. Although logistic regression appears to be the most commonly used method for estimating the propensity score, the use of bagging or boosting (Lee, Lessler, & Stuart, 2010; McCaffrey, Ridgeway, & Morral, 2004), recursive partitioning or tree-based methods (Lee et al., 2010; Setoguchi, Schneeweiss, Brookhart, Glynn, & Cook, 2008), random forests (Lee et al., 2010), and neural networks (Setoguchi et al., 2008) for estimating the propensity score have been examined.

Four different propensity score methods are used for removing the effects of confounding when estimating the effects of treatment on outcomes: propensity score matching, stratification (or subclassification) on the propensity score, inverse probability of treatment weighting (IPTW) using the propensity score, and covariate adjustment using the propensity score (Austin & Mamdani, 2006; Rosenbaum, 1987a; Rosenbaum & Rubin, 1983a). I describe each of these methods separately in the following subsections.

Rosenbaum and Rubin (1983a) defined treatment assignment to be strongly ignorable if the following two conditions hold: (a) (Y (1), Y(0)) ╩ Z|X and (b) 0 < P(Z = 1|X) < 1. The first condition says that treatment assignment is independent of the potential outcomes conditional on the observed baseline covariates. The second condition says that every subject has a nonzero probability to receive either treatment. They demonstrated that if treatment assignment is strongly ignorable, conditioning on the propensity score allows one to obtain unbiased estimates of average treatment effects. The aforementioned first condition is also referred to as the “no unmeasured confounders” assumption: the assumption that all variables that affect treatment assignment and outcome have been measured. Because this is the crucial assumption that underlies propensity score analyses, Rosenbaum and Rubin (1983b) proposed analyses to assess the sensitivity of study conclusions to the assumption that there were no unmeasured confounders that influenced treatment assignment. Furthermore, Rosenbaum (1987b) proposed the use of a second control group to examine the plausibility that adjustment for measured covariates has eliminated bias in estimating treatment effects. It should be noted that although the assumption of strongly ignorable treatment assignment/no unmeasured confounding is explicitly stated in the context of propensity score analyses, this assumption also underlies regression-based approaches for estimating treatment effects in observational studies.

Propensity Score Matching

Propensity score matching entails forming matched sets of treated and untreated subjects who share a similar value of the propensity score (Rosenbaum & Rubin, 1983a, 1985). Propensity score matching allows one to estimate the ATT (Imbens, 2004). The most common implementation of propensity score matching is one-to-one or pair matching, in which pairs of treated and untreated subjects are formed, such that matched subjects have similar values of the propensity score. Although one-to-one matching appears to be the most common approach to propensity score matching, other approaches can be used. These are discussed at the end of this section. Unless stated otherwise, the following discussion is in the context of 1:1 matching.

Once a matched sample has been formed, the treatment effect can be estimated by directly comparing outcomes between treated and untreated subjects in the matched sample. If the outcome is continuous (e.g., a depression scale), the effect of treatment can be estimated as the difference between the mean outcome for treated subjects and the mean outcome for untreated subjects in the matched sample (Rosenbaum & Rubin, 1983a). If the outcome is dichotomous (self-report of the presence or absence of depression), the effect of treatment can be estimated as the difference between the proportion of subjects experiencing the event in each of the two groups (treated vs. untreated) in the matched sample. With binary outcomes, the effect of treatment can also be described using the relative risk or the NNT (Austin, 2008a, 2010; Rosenbaum & Rubin, 1983a). Thus, the reporting of treatment effects can be done in same metrics as are commonly used in RCTs.

Once the effect of treatment has been estimated in the propensity score matched sample, the variance of the estimated treatment effect and its statistical significance can be estimated. Schafer and Kang (2008) suggest that, within the matched sample, the treated and untreated subjects should be regarded as independent. In contrast to this, Imbens (2004) suggests that, when using a matched estimator, the variance should be calculated using a method appropriate for paired experiments. I argue that the propensity score matched sample does not consist of independent observations. Rather, treated and untreated subjects within the same matched set have similar values of the propensity score. Therefore, their observed baseline covariates come from the same multivariate distribution. In the presence of confounding, baseline covariates are related to outcomes. Thus, matched subjects are more likely to have similar outcomes than are randomly selected subjects. The lack of independence in the propensity score matched sample should be accounted for when estimating the variance of the treatment effect. Recent studies using Monte Carlo simulations demonstrated that, for a range of scenarios, variance estimators that account for matching more accurately reflected the sampling variability of the estimated treatment effect (Austin 2009c, in press). Thus, a paired t test could be used for assessing the statistical significance of the effect of treatment on a continuous outcome. Similarly, McNemar's test can be used to assess the statistical significance of a difference in proportions for a dichotomous outcome.

The analysis of a propensity score matched sample can mimic that of an RCT: one can directly compare outcomes between treated and untreated subjects within the propensity score matched sample. In the context of an RCT, one expects that, on average, the distribution of covariates will be similar between treatment groups. However, in individual RCTs, residual differences in baseline covariates may exist between treatment groups. Regression adjustment can be used to reduce bias due to residual differences in observed baseline covariates between treatment groups. Regression adjustment results in increased precision for continuous outcomes and increased statistical power for continuous, binary, and time-to-event outcomes (Steyerberg, 2009). Similarly, in propensity score matched samples, covariate balance is a large sample property. Propensity score matching can be combined with additional matching on prognostic factors or regression adjustment (Imbens, 2004; Rubin & Thomas, 2000).

I now discuss different methods for forming matched pairs of treated and untreated subjects when matching on the propensity score. In doing so, several decisions must be made. First, one must choose between matching without replacement and matching with replacement (Rosenbaum, 2002). When using matching without replacement, once an untreated subject has been selected to be matched to a given treated subject, that untreated subject is no longer available for consideration as a potential match for subsequent treated subjects. As a result, each untreated subject is included in at most one matched set. In contrast, matching with replacement allows a given untreated subject to be included in more than one matched set. When matching with replacement is used, variance estimation must account for the fact that the same untreated subject may be in multiple matched sets (Hill & Reiter, 2006).

A second choice is between greedy and optimal matching (Rosenbaum, 2002). In greedy matching, a treated subject is first selected at random. The untreated subject whose propensity score is closest to that of this randomly selected treated subject is chosen for matching to this treated subject. This process is then repeated until untreated subjects have been matched to all treated subjects or until one has exhausted the list of treated subjects for whom a matched untreated subject can be found. This process is called greedy because at each step in the process, the nearest untreated subject is selected for matching to the given treated subject, even if that untreated subject would better serve as a match for a subsequent treated subject. An alternative to greedy matching is optimal matching, in which matches are formed so as to minimize the total within-pair difference of the propensity score. Gu and Rosenbaum (1993) compared greedy and optimal matching and found that optimal matching did no better than greedy matching in producing balanced matched samples.

In the previous paragraphs I described two sets of options for forming propensity score matched sets. However, I have not provided criteria for selecting untreated subjects whose propensity score is “close” to that of a treated subject. There are two primary methods for this: nearest neighbor matching and nearest neighbor matching within a specified caliper distance (Rosenbaum & Rubin, 1985). Nearest neighbor matching selects for matching to a given treated subject that untreated subject whose propensity score is closest to that of the treated subject. If multiple untreated subjects have propensity scores that are equally close to that of the treated subject, one of these untreated subjects is selected at random. It is important to note that no restrictions are placed upon the maximum acceptable difference between the propensity scores of two matched subjects.

Nearest neighbor matching within a specified caliper distance is similar to nearest neighbor matching with the further restriction that the absolute difference in the propensity scores of matched subjects must be below some prespecified threshold (the caliper distance). Thus, for a given treated subject, one would identify all the untreated subjects whose propensity score lay within a specified distance of that of the treated subject. From this restricted set of untreated subjects, the untreated subject whose propensity score was closest to that of the treated subject would be selected for matching to this treated subject. If no untreated subjects had propensity scores that lay within the specified caliper distance of the propensity score of the treated subject, that treated subject would not be matched with any untreated subject. The unmatched treated subject would then be excluded from the resultant matched sample.

When using caliper matching, there is no uniformly agreed upon definition of what constitutes a maximal acceptable distance. Indeed, in the medical literature, a wide range of caliper widths have been used (Austin, 2007a, 2008b). Cochran and Rubin (1973) examined the reduction in bias due to a single normally distributed confounding variable by matching on this confounding variable using calipers whose widths were proportional to the standard deviation of the confounding variable. Based on these results, there are theoretical arguments for matching on the logit of the propensity score, as this quantity is more likely to be normally distributed, and for using a caliper width that is a proportion of the standard deviation of the logit of the propensity score. Building on the prior work of Cochran and Rubin on matching on a single normally distributed confounding variable, Rosenbaum and Rubin (1985) suggested that similar reduction in bias can be achieved by matching on the logit of the propensity score using caliper widths similar to those described by Cochran and Rubin. For instance, if the variance of the logit of the propensity score in the treated subjects is the same as the variance in the untreated subjects, using calipers of width equal to 0.2 of the pooled standard deviation of the logit of the propensity score will eliminate approximately 99% of the bias due to the measured confounders. Recently, Austin (201 1b) examined optimal caliper widths when estimating risk differences and differences in means. It was suggested that researchers use a caliper of width equal to 0.2 of the standard deviation of the logit of the propensity score as this value (or one close to it) minimized the mean squared error of the estimated treatment effect in several scenarios.

In this paragraph, I briefly describe alternatives to one-to-one pair matching when matching on the propensity score and refer the reader to the cited articles. In many-to-one (M: l) matching, M untreated subjects are matched to each treated subject. Ming and Rosenbaum (2000) modified this approach by allowing for a variable number of untreated subjects to be matched to each treated subject. They found that improved bias reduction was obtained when matching with a variable number of controls compared to matching with a fixed number of controls. Full matching (Gu & Rosenbaum, 1993; Hansen, 2004; Rosenbaum, 1991) involves forming matched sets consisting of either one treated subject and at least one untreated subject or one untreated subject and at least one treated subject. The reader is referred to Gu and Rosenbaum for an in-depth comparison of different matching methods.

Propensity score matching can be conducted using a variety of statistical packages. Methods to conduct propensity score matching using SAS® are described in Chapter 3 of Faries, Leon, Maria Haro, and Obenchain (2010). In R, the Matching (Sekhon, in press), Matchlt (Ho, Imai, King, & Stuart, 2011), and Optmatch (Hansen & Klopfer, 2006) packages allow one to implement a variety of different matching methods. In Stata®, the PSMATCH2 module can be used for propensity score matching.

Stratification on the Propensity Score

Stratification on the propensity score involves stratifying subjects into mutually exclusive subsets based on their estimated propensity score. Subjects are ranked according to their estimated propensity score. Subjects are then stratified into subsets based on previously defined thresholds of the estimated propensity score. A common approach is to divide subjects into five equal-size groups using the quintiles of the estimated propensity score. Cochran (1968) demonstrated that stratifying on the quintiles of a continuous confounding variable eliminated approximately 90% of the bias due to that variable. Rosenbaum and Rubin (1984) extended this result to stratification on the propensity score, stating that stratifying on the quintiles of the propensity score eliminates approximately 90% of the bias due to measured confounders when estimating a linear treatment effect. Increasing the number of strata used should result in improved bias reduction, although the marginal reduction in bias decreases as the number of strata increases (Cochran, 1968; Huppler Hullsiek & Louis, 2002). Within each propensity score stratum, treated and untreated subjects will have roughly similar values of the propensity score. Therefore, when the propensity score has been correctly specified, the distribution of measured baseline covariates will be approximately similar between treated and untreated subjects within the same stratum.

Stratification on the propensity can be conceptualized as a meta-analysis of a set of quasi-RCTs. Within each stratum, the effect of treatment on outcomes can be estimated by comparing outcomes directly between treated and untreated subjects. The stratum-specific estimates of treatment effect can then be pooled across stratum to estimate an overall treatment effect (Rosenbaum & Rubin, 1984). Thus, stratum-specific differences in means or risk differences can be estimated. These can be averaged to produce an overall difference in means or risk difference. In general, stratum-specific estimates of effect are weighted by the proportion of subjects who lie within that stratum. Thus, when the sample is stratified into K equal-size strata, stratum-specific weights of 1/K are commonly used when pooling the stratum-specific treatment effects, allowing one to estimate the ATE (Imbens, 2004). The use of stratum-specific weights that are equal to that proportion of treated subjects that lie within each stratum allow one to estimate the ATT (Imbens, 2004). A pooled estimate of the variance of the estimated treatment effect can be obtained by pooling the variances of the stratum-specific treatment effects. For a greater discussion of variance estimation, the reader is referred to Rosenbaum and Rubin (1984) and Lunceford and Davidian (2004). As with matching, within-stratum regression adjustment may be used to account for residual differences between treated and untreated subjects (Imbens, 2004; Lunceford & Davidian, 2004).

Inverse Probability of Treatment Weighting Using the Propensity Score

Inverse probability of treatment weighting (IPTW) using the propensity score uses weights based on the propensity score to create a synthetic sample in which the distribution of measured baseline covariates is independent of treatment assignment. The use of IPTW is similar to the use of survey sampling weights that are used to weight survey samples so that they are representative of specific populations (Morgan & Todd, 2008).

As mentioned earlier, let Zi be an indicator variable denoting whether or not the ith subject was treated; furthermore, let ei denote the propensity score for the ith subject. Weights can be defined as 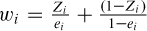Inline graphic. A subject's weight is equal to the inverse of the probability of receiving the treatment that the subject actually received. Inverse probability of treatment weighting was first proposed by Rosenbaum (1987a) as a form of model-based direct standardization.

Lunceford and Davidian (2004) review a variety of estimators for treatment effects based on IPTW. Assume that Yi denotes the outcome variable measured on the ith subject. An estimate of the ATE is 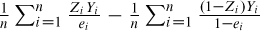Inline graphic, where n denotes the number of subjects. Lunceford and Davidian describe the theoretical properties of this estimator (along with other IPTW estimators) of the ATE and compare their performance to stratification.

Joffe, Ten Have, Feldman, and Kimmel (2004) describe how regression models can be weighted by the inverse probability of treatment to estimate causal effects of treatments. When used in this context, IPTW is part of a larger family of causal methods known as marginal structural model (Hernan, Brumback, & Robins, 2000, 2002). It is important to note that variance estimation must account for the weighted nature of the synthetic sample, with robust variance estimation commonly being used to account for the sample weights (Joffe et al., 2004).

The weights may be inaccurate or unstable for subjects with a very low probability of receiving the treatment received. To address this issue, the use of stabilizing weights has been proposed (Robins, Hernan, & Brumback, 2000). The weights described earlier allow one to estimate the ATE. However, using weights equal to 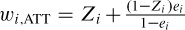Inline graphic allows one to estimate the ATT, whereas the use of weights equal to 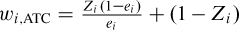Inline graphic allows one to estimate the average effect of treatment in the controls (Morgan & Todd, 2008).

Covariate Adjustment Using the Propensity Score

The fourth propensity score method is covariate adjustment using the propensity score. Using this approach, the outcome variable is regressed on an indicator variable denoting treatment status and the estimated propensity score. The choice of regression model would depend on the nature of the outcome. For continuous outcomes, a linear model would be chosen; for dichotomous outcomes, a logistic regression model may be selected. The effect of treatment is determined using the estimated regression coefficient from the fitted regression model. For a linear model, the treatment effect is an adjusted difference in means, whereas for a logistic model it is an adjusted odds ratio. Of the four propensity score methods, this is the only one that requires that a regression model relating the outcome to treatment status and a covariate (the propensity score) be specified. Furthermore, this method assumes that the nature of the relationship between the propensity score and the outcome has been correctly modeled.

Comparison of the Different Propensity Score Methods

Several studies have demonstrated that propensity score matching eliminates a greater proportion of the systematic differences in baseline characteristics between treated and untreated subjects than does stratification on the propensity score or covariate adjustment using the propensity score (Austin, 2009a; Austin, Grootendorst, & Anderson, 2007; Austin & Mamdani, 2006). In some settings propensity score matching and IPTW removed systematic differences between treated and untreated subjects to a comparable degree; however, in some settings, propensity score matching removed modestly more imbalance than did IPTW (Austin, 2009a). Lunceford and Davidian (2004) demonstrated that stratification results in estimates of average treatment effects with greater bias than does a variety of weighted estimators.

Propensity score matching, stratification on the propensity score, and IPTW differ from covariate adjustment using the propensity score in that the three former methods separate the design of the study from the analysis of the study; this separation does not occur when covariate adjustment using the propensity score is used. Appropriate diagnostics exist for each of the four propensity score methods to assess whether the propensity score model has been adequately specified. However, with propensity score matching, stratification on the propensity score, and IPTW, once one is satisfied with the specification of the propensity score model, one can directly estimate the effect of treatment on outcomes in the matched, stratified, or weighted sample. Specification of a regression model relating the outcome to treatment is not necessary. In contrast, when using covariate adjustment using the propensity score, once one is satisfied that the propensity score model has been adequately specified, one must fit a regression model relating the outcome to an indicator variable denoting treatment status and to the propensity score. In specifying the regression model, one must correctly model the relationship between the propensity score and the outcome (e.g., specifying whether the relationship is linear or nonlinear). In doing so, the outcome is always in sight because the outcome model contains both the propensity score and the outcome. As Rubin (2001) notes, when using regression modeling, the temptation to work toward the desired or anticipated result is always present. Another difference between the four propensity score approaches is that covariate adjustment using the propensity score and IPTW may be more sensitive to whether the propensity score has been accurately estimated (Rubin, 2004).

The reader is referred elsewhere to empirical studies comparing the results of analyses using the different propensity score methods on the same data set (Austin & Mamdani, 2006; Kurth et al., 2006). Prior Monte Carlo studies have compared the relative performance of the different propensity score methods for estimating risk differences, relative risks, and marginal and conditional odds ratios (Austin, 2007b, 2008c, 2010; Austin, Grootendorst, Normand, & Anderson, 2007). It is important to note that two of these studies found that stratification, matching, and covariate adjustment using the propensity score resulted in biased estimation of both conditional and marginal odds ratios.

BALANCE DIAGNOSTICS

The true propensity score is a balancing score: conditional on the true propensity score, the distribution of measured baseline covariates is independent of treatment assignment. In an observational study the true propensity score is not known. It must be estimated using the study data. An important component of any propensity score analysis is examining whether the propensity score model has been adequately specified. In this section, I discuss methods for assessing whether the propensity score model has been adequately specified.

The true propensity score is a balancing score. Therefore, in strata of subjects that have the same propensity score, the distribution of measured baseline covariates will be the same between treated and untreated subjects. Appropriate methods for assessing whether the propensity score model has been adequately specified involve examining whether the distribution of measured baseline covariates is similar between treated and untreated subjects with the same estimated propensity score. If, after conditioning on the propensity score, there remain systematic differences in baseline covariates between treated and untreated subjects, this can be an indication that the propensity score model has not been correctly specified. With propensity score matching, assessing whether the propensity score model has been adequately specified involves comparing treated and untreated subjects within the propensity score matched sample. For IPTW this assessment involves comparing treated and untreated subjects in the sample weighted by the inverse probability of treatment. For stratification on the propensity score, this assessment entails comparing treated and untreated subjects within strata of the propensity score.

In this section, I summarize an extensive previous discussion of methods for assessing the comparability of treated and untreated subjects in a propensity score matched sample (Austin, 2009b). The methods described are for use in the context of one-to-one matching on the propensity score. Adaptations for use with many-to-one matching on the propensity score are provided elsewhere (Austin, 2008d). These methods can be readily adapted to stratification on the propensity score and IPTW using the propensity score (see Joffe et al., 2004; Morgan & Todd, 2008, for use with IPTW). Goodness-of-fit diagnostics for use with covariate adjustment using the propensity score are provided elsewhere (Austin, 2008e).

Comparing the similarity of treated and untreated subjects in the matched sample should begin with a comparison of the means or medians of continuous covariates and the distribution of their categorical counterparts between treated and untreated subjects. The standardized difference can be used to compare the mean of continuous and binary variables between treatment groups (multilevel categorical variables can be represented using a set of binary indicator variables; Austin, 2009e; Flury & Riedwyl, 1986). For a continuous covariate, the standardized difference is defined as

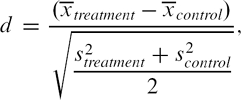graphic file with name hmbr46-399_mu1.jpg

where 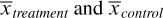Inline graphic denote the sample mean of the covariate in treated and untreated subjects, respectively, whereas s2treatment and s2control denote the sample variance of the covariate in treated and untreated subjects, respectively. For dichotomous variables, the standardized difference is defined as

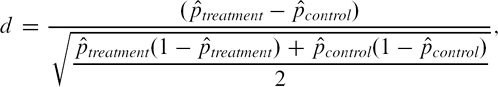graphic file with name hmbr46-399_mu2.jpg

where 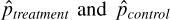Inline graphic denote the prevalence or mean of the dichotomous variable in treated and untreated subjects, respectively. The standardized difference compares the difference in means in units of the pooled standard deviation. Furthermore, it is not influenced by sample size and allows for the comparison of the relative balance of variables measured in different units. Although there is no universally agreed upon criterion as to what threshold of the standardized difference can be used to indicate important imbalance, a standard difference that is less than 0.1 has been taken to indicate a negligible difference in the mean or prevalence of a covariate between treatment groups (Normand et al., 2001).

The standardized difference provides a framework for comparing the mean or prevalence of a baseline covariate between treatment groups in the propensity score matched sample. However, a thorough examination of the comparability of treated and untreated subjects in the propensity score matched sample should not stop with a comparison of means and prevalences. The true propensity score is a balancing score: within strata matched on the true propensity score, the distribution of observed baseline covariates is independent of treatment status. Thus, the entire distribution of baseline covariates, not just means and prevalences, should be similar between treatment groups in the matched sample. Therefore, higher order moments of covariates and interactions between covariates should be compared between treatment groups (Austin, 2009b; Ho, Imai, King, & Stuart, 2007; Imai, King, & Stuart, 2008; Morgan & Todd, 2008). Similarly, graphical methods such as side-by-side boxplots, quantile-quantile plots, cumulative distribution functions, and empirical nonparametric density plots can be used to compare the distribution of continuous baseline covariates between treatment groups in the propensity score matched sample (Austin, 2009b).

Rosenbaum and Rubin (1984) describe an iterative approach to specifying a propensity score model (stratification on the propensity score was used in their illustration; in this paragraph I describe how one would proceed when using propensity score matching). One begins by specifying an initial propensity score model. The comparability of treated and untreated subjects in the resultant matched sample is then assessed. If important residual systematic differences between treated and untreated subjects are found to remain, the initial propensity score model can be modified. One can modify the propensity score by including additional covariates, by adding interactions between covariates that are already in the model, or by modeling the relationship between continuous covariates and treatment status using nonlinear terms (e.g., using cubic smoothing splines). One proceeds in an iterative fashion until systematic differences in observed baseline covariates between treated and untreated subjects have either been eliminated or reduced to an acceptable level. It is important to note that at each step of the iterative process, one is not guided by the statistical significance of the estimated regression coefficients in the propensity score model (assuming one is using a logistic regression model). Rather, one is working toward the objective of creating a matched sample in which the distribution of observed baseline covariates is similar between treated and untreated subjects.

Rubin (2001) proposed a set of criteria based on comparing the distribution of the propensity score between treated and untreated subjects in a sample to determine whether regression adjustment may inadequately eliminate bias when comparing outcomes between treatment groups. Some authors have suggested that the comparison of baseline covariates may be complemented by comparing the distribution of the estimated propensity score between treated and untreated subjects in the matched sample (Ho et al., 2007). This approach may be useful for determining the common area of support or the degree of overlap in the propensity score between treated and untreated subjects. Furthermore, it may serve as a rough assessment of whether the means of covariates included in the propensity score model are similar between treatment groups. However, recent research has found that this approach is insufficient for determining whether an important variable has been omitted from the propensity score model or for assessing whether the propensity score model has been correctly specified (Austin, 2009b). For instance, in a sample matched on a misspecified propensity score, the mean of an interaction between two covariates was unbalanced between treatment groups. Despite this imbalance, the distribution of the misspecified propensity score was similar to that of the correctly specified propensity score.

Applied authors have frequently used statistical significance testing to compare the mean of continuous covariates or the distribution of categorical variables between treated and untreated subjects in propensity score matched samples (Austin, 2007a, 2008b, 2008c). This approach has been criticized by several authors for two reasons (Imai et al., 2008; Austin, 2008b, 2009b). First, significance levels are confounded with sample size. The propensity score matched sample is almost invariably smaller than the original sample. Thus, relying on significance testing to detect imbalance may produce misleading results; findings of nonsignificant differences between groups may be due only to the diminished sample size of the matched sample (furthermore, for large samples, statistically significant differences may be found merely due to the high power of the test when covariate means are trivially different). Second, Imai et al. suggested that balance is a property of a particular sample and that reference to a superpopulation is inappropriate. For these reasons, the use of statistical significance testing to assess balance in propensity score matched samples is discouraged.

Finally, a recent review of propensity score methods (Stürmer et al., 2006) documented that many authors report the c-statistic of the propensity score model. The c-statistic indicates the degree to which the propensity score model discriminates between subjects who are treated and those who are untreated. Recent research has indicated that this statistic provides no information as to whether the propensity score model has been correctly specified (Austin, 2009b; Austin, Grootendorst, & Anderson, 2007; Weitzen, Lapane, Toledano, Hume, & Mor, 2005).

VARIABLE SELECTION FOR THE PROPENSITY SCORE MODEL

There is a lack of consensus in the applied literature as to which variables to include in the propensity score model. Possible sets of variables for inclusion in the propensity score model include the following: all measured baseline covariates, all baseline covariates that are associated with treatment assignment, all covariates that affect the outcome (i.e., the potential confounders), and all covariates that affect both treatment assignment and the outcome (i.e., the true confounders). The propensity score is defined to be the probability of treatment assignment (ei, = Pr(Zi, = 1|Xi)). Thus, there are theoretical arguments in favor of the inclusion of only those variables that affect treatment assignment.

A recent study (Austin, Grootendorst, & Anderson, 2007) examined the relative benefits of including the different sets of baseline covariates described earlier in the propensity score model. It was shown that there were merits to including only the potential confounders or the true confounders in the propensity score model. In the context of propensity-score matching, the use of any of the four different sets of covariates in the propensity score model resulted in all prognostically important variables being balanced between treated and untreated subjects in the matched sample. When only the potential confounders or only the true confounders were included in the propensity score model, the variables that were imbalanced between treated and untreated subjects were those variables that affected treatment assignment but that were independent of the outcome. However, a greater number of matched pairs were formed when these two propensity score models were used compared with when the two alternative propensity score models were used. Furthermore, these two propensity score models (i.e., the potential confounders or the true confounders) resulted in estimates of a null treatment effect that had lower mean squared error compared with estimates obtained when the other two propensity score models were used. Thus, using these two propensity score models did not result in the introduction of additional bias but resulted in estimates of treatment effect with greater precision. Similar findings were observed by Brookhart et al. (2006), who suggested that variables that do not affect exposure but that affect the outcome should always be included in the propensity score model. Furthermore, they noted that including variables that affect exposure but not the outcome will increase the variance of the estimated treatment effect without a concomitant reduction in bias.

It should be noted that, in practice, it may be difficult to accurately classify baseline variables into the true confounders, those that only affect the outcome, those that only affect exposure, and those that affect neither treatment nor the outcome. In specific settings, the published literature may provide some guidance for identifying variables that affect the outcome. In practice, in many settings, most subject-level baseline covariates likely affect both treatment assignment and the outcome. Therefore, in many settings, it is likely that one can safely include all measured baseline characteristics in the propensity score model. Variables that may require greater investigation are policy-related variables or variables denoting different temporal periods. For instance, in a study comparing the affect of an older treatment with that of a newer treatment, subjects who entered the study in an earlier period may be more likely to receive the older treatment, whereas subjects who entered the study in a later period may be more likely to receive the newer treatment. Thus a variable denoting a temporal period would affect treatment assignment. However, if the outcome was conditionally independent of temporal period, the inclusion of a variable denoting temporal period in the propensity score model could result in the formation of fewer matched pairs compared with if this variable were excluded from the propensity score model (e.g., the examination of the effect of atypical vs. typical neuroleptic agents on death in elderly nursing home residents with dementia; Austin, Grootendorst, & Anderson, 2007). Finally, one should stress that the propensity score model should only include variables that are measured at baseline and not post-baseline covariates that may be influenced or modified by the treatment.

PROPENSITY SCORE METHODS VERSUS REGRESSION ADJUSTMENT

Historically, regression adjustment has been used more frequently than propensity score methods for estimating the effects of treatments when using observational data. In this section, I compare and contrast these two competing methods for inference.

Conditional Versus Marginal Estimates of Treatment Effect

A conditional treatment effect is the average effect of treatment on the individual. A marginal treatment effect is the average effect of treatment on the population. A measure of treatment effect is said to be collapsible if the conditional and marginal effects coincide. For instance, in the absence of confounding, the difference in means and risk difference are collapsible (Greenland, 1987). Thus, an intervention that, on average, increases a student's test score by five units will, if applied to the entire population, increase the population's test scores by five units compared with if the intervention were withheld from the entire population.

Thus, in a randomized controlled trial, in which all covariates were balanced between treatment groups, the crude difference in means and the adjusted difference in means will coincide. Propensity score methods allow for estimation of the marginal treatment effect (Rosenbaum, 2005). Thus, in an observational study in which (a) there was no unmeasured confounding, (b) the outcome was continuous, and (c) the true outcome model was known, the marginal and conditional estimates would coincide. Assuming that both the outcome regression model and the propensity score model were correctly specified, it follows that propensity score methods should result in conclusions similar to those obtained using linear regression adjustment.

However, when the outcome is either binary or time-to-event in nature and if the odds ratio or the hazard ratio is used as the measure of treatment effect, then, even in the absence of confounding, the marginal and conditional estimates of the treatment effect need not coincide (Gail, Wieand, & Piantadosi, 1984; Greenland, 1987). Thus, in an observational study, even in the absence of unmeasured confounding, and even if the true outcome regression model were known, the conditional odds ratio or the conditional hazard ratio need not coincide with the estimate obtained using propensity score methods. This phenomenon was examined in greater depth in the context of propensity score methods in a previous study (Austin, Grootendorst, Normand, et al., 2007). When data were simulated to induce a specific conditional odds ratio or hazard ratio, propensity score methods were found to result in biased estimation, even when the true propensity score model was used. These findings from a Monte Carlo simulation mirror those from an empirical study that examined articles published in the medical literature that reported using both regression adjustment and propensity score methods to estimate treatment effects (Shah, Laupacis, Hux, & Austin, 2005). Although similar effect sizes were reported, estimates obtained using propensity score methods tended to be modestly closer to the null compared with when regression-based approaches were used for estimating odds ratios or hazard ratios.

The aforementioned suggest that researchers need to carefully distinguish between marginal and conditional treatment effects. In part, study design and the analytic plan should reflect which treatment effect is more meaningful in a given context. However, researchers should note that both RCTs and propensity score methods allow one to estimate marginal treatment effects. Thus, if the objective of an observational study is to answer the same question as an RCT, the marginal effect may be of greater interest to researchers using observational data.

Regression Adjustment Versus Propensity Score Methods: Practical Concerns

There are several practical reasons for preferring the use of propensity score-based methods to regression-based methods when estimating treatment effects using observational data. First, it is simpler to determine whether the propensity score model has been adequately specified than to assess whether the regression model relating treatment assignment and baseline covariates to the outcome has been correctly specified. The propensity score is a balancing score: conditional on the propensity score, the distribution of measured baseline covariates is similar between treated and untreated subjects. In a previous section I described diagnostics for assessing whether the propensity score model has been adequately specified. These diagnostics were based on comparing the distribution of measured baseline covariates between treated and untreated subjects, either in the propensity score matched sample, within strata of the propensity score, or within the weighted sample. In contrast, it is much more difficult to determine whether the regression model relating treatment selection and baseline covariates to the outcome has been correctly specified. Goodness-of-fit measures, such as model R2, do not provide a test of whether the outcome model has been correctly specified. Furthermore, goodness-of-fit tests do not allow one to determine the degree to which the fitted regression model has successfully eliminated systematic differences between treated and untreated subjects.

Second, these methods allow one to separate the design of the study from the analysis of the study. This is similar to an RCT, in which the study is designed first; only after the study has been completed is the effect of treatment on the outcome estimated. When using propensity score matching, stratification on the propensity score, and IPTW using the propensity score, the propensity score can be estimated and a matched, stratified, or weighted sample can be constructed without any reference to the outcome. Only once acceptable balance in measured baseline covariates has been achieved does one progress to estimating the effect of treatment on the outcome. However, when using regression adjustment, the outcome is always in sight, and the researcher is faced with the subtle temptation to continually modify the regression model until the desired association has been achieved (Rubin, 2001). When using matching, stratification, or weighting using the propensity score, subsequent regression adjustment may be used to eliminate residual imbalance in prognostically important covariates. However, as in an RCT, this regression may be specified prior to the analysis.

Third, there may be increased flexibility when outcomes (when binary or time-to-event in nature) are rare and treatment is common (Braitman & Rosenbaum, 2002). When outcomes are either binary or time-to-event in nature, prior research has suggested that at least 10 events should be observed for every covariate that is entered into a regression model (Peduzzi, Concato, Feinstein, & Holford, 1995; Peduzzi, Concato, Kemper, Holford, & Feinstein, 1996). Thus, in some settings, insufficient outcomes may be observed to allow one to adequately adjust for all baseline variables that one would like to include in the regression model. However, if the occurrence of treatment or nontreatment is more common than outcomes, there may be increased flexibility in modeling the propensity score.

Fourth, one can explicitly examine the degree of overlap in the distribution of baseline covariates between the two treatment groups. When using propensity score matching and stratification, one is explicitly comparing outcomes between treated and untreated subjects who have a similar distribution of observed baseline covariates. If there are substantial differences in baseline covariates between treated and untreated subjects, this will be evident by either the small number of matched subjects or by the observation that most strata consist primarily of either treated subjects or primarily of untreated subjects. When faced with the sparse overlap between the treated and untreated subjects, the analyst is faced with a choice between two alternatives: first, to restrict the analysis to comparing outcomes between the minority of treated and untreated subjects who have similar covariate patterns, and second, to discontinue the analysis, concluding that treated and untreated subjects are so different that a meaningful comparison of outcomes between the two groups is not plausible. When using regression-based approaches, it may be difficult to assess the degree of overlap between the distribution of baseline covariates for the two groups. In a setting in which there is a strong separation between the two groups, a naïve analyst may proceed with a regression-based analysis without being aware that the fitted regression model is interpolating between two distinct populations.

DISCUSSION

In this article I have introduced the concept of the propensity score and described how its use can allow one to design and analyze an observational study so as to mimic some of the characteristics of a randomized study. First, the propensity score is a balancing score: conditional on the propensity score, the distribution of observed baseline covariates is similar between treated and untreated subjects. Thus, just as randomization will, on average, result in both measured and unmeasured covariates being balanced between treatment groups, so conditioning on the propensity score will, on average, result in measured baseline covariates being balanced between treatment groups. However, it should be reinforced that conditioning on the propensity score need not balance unmeasured covariates (Austin, Mamdani, Stukel, Anderson, & Tu, 2005). Second, propensity score methods allow one to separate the design of an observational study from its analysis (Rubin, 2007). Third, similar to RCTs, propensity score methods allow one to estimate marginal (or population-average) treatment effects. This is in contrast to regression-based approaches that allow one to estimate conditional (or adjusted) estimates of treatment effects. Fourth, propensity score methods allow one to estimate treatment effects in metrics similar to those reported in RCTs. When outcomes are binary, one can report risk differences, numbers needed to treat, or the relative risk. Whereas, the odds ratio is most commonly reported when logistic regression models are used.

In this article, I have also paid attention to a frequently overlooked aspect of study design: assessing whether the propensity score model has been adequately specified. Methods for assessing the specification of the propensity score model are based on comparing the distribution of measured baseline covariates between treated and untreated subjects with similar values of the propensity score. I have also argued that balance diagnostics for assessing the specification of the propensity score are more transparent than are comparable diagnostics for assessing whether an outcome regression model has been correctly formulated. Similarly, with propensity score methods, one can more easily assess whether observed confounding has been adequately eliminated, whereas this is more difficult to assess when regression-based approaches are used.

This article was intended to provide an introductory overview of propensity score methods. The reader is referred to the following books for a more in-depth discussion (Guo & Fraser, 2009; Morgan & Winship, 2007; Rosenbaum, 2002, 2010; Rubin, 2006). Similarly, the reader is referred to previous introductory overview articles (D'Agostino, 1998; Luellen, Shadish, & Clark, 2005; Rosenbaum, 2005; Rubin, 1997; Schafer & Kang, 2008). In a recently published tutorial and case study in this journal, I illustrated the application of propensity score methods to address a specific research question (Austin, 201 la).

In conclusion, propensity score methods allow one to transparently design and analyze observational studies. I encourage greater use of these methods in applied psychological and behavioral research.

ACKNOWLEDGMENTS

This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC). The opinions, results, and conclusions reported in this article are those of the author and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred. Peter C. Austin is supported in part by a Career Investigator award from the Heart and Stroke Foundation of Ontario. This study was supported in part by an operating grant from the Canadian Institutes of Health Research (MOP 86508).

REFERENCES

  1. Austin P.C. Propensity-score matching in the cardiovascular surgery literature from 2004 to 2006: A systematic review and suggestions for improvement. Journal of Thoracic and Cardiovascular Surgery. 2007a;134:1128–1135. doi: 10.1016/j.jtcvs.2007.07.021. doi:10.1016/j.jtcvs.2007.07.021. [DOI] [PubMed] [Google Scholar]
  2. Austin P.C. The performance of different propensity score methods for estimating marginal odds ratios. Statistics in Medicine. 2007b;26:3078–3094. doi: 10.1002/sim.2781. doi:10.1002/sim.2781. [DOI] [PubMed] [Google Scholar]
  3. Austin P.C. The performance of different propensity score methods for estimating relative risks. Journal of Clinical Epidemiology. 2008a;61:537–545. doi: 10.1016/j.jclinepi.2007.07.011. doi:10.1016/j.jclinepi.2007.07.011. [DOI] [PubMed] [Google Scholar]
  4. Austin P.C. A critical appraisal of propensity score matching in the medical literature from 1996 to 2003. Statistics in Medicine. 2008b;27:2037–2049. doi: 10.1002/sim.3150. doi:10.1002/sim.3150. [DOI] [PubMed] [Google Scholar]
  5. Austin P.C. A report card on propensity-score matching in the cardiology literature from 2004 to 2006: Results of a systematic review. Circulation: Cardiovascular Quality and Outcomes. 2008c;1:62–67. doi: 10.1161/CIRCOUTCOMES.108.790634. doi:10.1161/CIRCOUTCOMES.108.790634. [DOI] [PubMed] [Google Scholar]
  6. Austin P.C. Assessing balance in baseline covariates when using many-to-one matching on the propensity-score. Pharmacoepidemiology and Drug Safety. 2008d;17:1218–1225. doi: 10.1002/pds.1674. doi:10.1002/ pds.1674. [DOI] [PubMed] [Google Scholar]
  7. Austin P.C. Goodness-of-fit diagnostics for the propensity score model when estimating treatment effects using covariate adjustment with the propensity score. Pharmacoepidemiology and Drug Safety. 2008e;17:1202–1217. doi: 10.1002/pds.1673. doi:10.1002/pds.1673. [DOI] [PubMed] [Google Scholar]
  8. Austin P.C. Type I error rates, coverage of confidence intervals, and variance estimation in propensity-score matched analyses. The International Journal of Biostatistics. 2009a;5 doi: 10.2202/1557-4679.1146. Article 13. doi:10.2202/1557-4679.1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Austin P.C. The relative ability of different propensity-score methods to balance measured covariates between treated and untreated subjects in observational studies. Medical Decision Making. 2009b;29:661–677. doi: 10.1177/0272989X09341755. doi:10.1177/0272989X09341755. [DOI] [PubMed] [Google Scholar]
  10. Austin P.C. Balance diagnostics for comparing the distribution of baseline covariates between treatment groups in propensity-score matched samples. Statistics in Medicine. 2009c;28:3083–3107. doi: 10.1002/sim.3697. doi:10.1002/sim.3697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Austin P.C. Using the standardized difference to compare the prevalence of a binary variable between two groups in observational research. Communications in Statistics— Simulation and Computation. 2009d;38:1228–1234. .doi:10.1080/03610910902859574. [Google Scholar]
  12. Austin P.C. The performance of different propensity score methods for estimating difference in proportions (risk differences or absolute risk reductions) in observational studies. Statistics in Medicine. 2010;29:2137–2148. doi: 10.1002/sim.3854. doi:10.1002/sim.3854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Austin P.C. A tutorial and case study in propensity score analysis: An application to estimating the effect of in-hospital smoking cessation counseling on mortality. Multivariate Behavioral Research. 2011a;46:119–151. doi: 10.1080/00273171.2011.540480. doi:10.1080/00273171.2011.540480. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Austin P.C. Optimal caliper widths for propensity-score matching when estimating differences in means and differences in proportions in observational studies. Pharmaceutical Statistics. 2011b;10:150–161. doi: 10.1002/pst.433. doi:10.1002/pst.433. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Austin P.C. Comparing paired vs. non-paired statistical methods of analyses when making inferences about absolute risk reductions in propensity-score matched samples, Statistics in Medicine. in press. doi:10.1002/sim.4200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Austin P.C., Grootendorst P., Anderson G.M. A comparison of the ability of different propensity score models to balance measured variables between treated and untreated subjects: A Monte Carlo study. Statistics in Medicine. 2007;26:734–753. doi: 10.1002/sim.2580. doi:10.1002/sim.2580. [DOI] [PubMed] [Google Scholar]
  17. Austin P.C., Grootendorst P., Normand S.L. T., Anderson G.M. Conditioning on the propensity score can result in biased estimation of common measures of treatment effect: A Monte Carlo study. Statistics in Medicine. 2007;26:754–768. doi: 10.1002/sim.2618. doi:10.1002/sim.2618. [DOI] [PubMed] [Google Scholar]
  18. Austin P.C., Mamdani M.M. A comparison of propensity score methods: A case-study estimating the effectiveness of post-AMI statin use. Statistics in Medicine. 2006;25:2084–2106. doi: 10.1002/sim.2328. doi: 10.1002/sim.2328. [DOI] [PubMed] [Google Scholar]
  19. Austin P.C., Mamdani M.M., Stukel T.A., Anderson G.M., Tu J.V. The use of the propensity score for estimating treatment effects: Administrative versus clinical data. Statistics in Medicine. 2005;24:1563–1578. doi: 10.1002/sim.2053. doi:10.1002/sim.2053. [DOI] [PubMed] [Google Scholar]
  20. Braitman L.E., Rosenbaum P.R. Rare outcomes, common treatments: Analytic strategies using propensity scores. Annals of Internal Medicine. 2002;137:693–695. doi: 10.7326/0003-4819-137-8-200210150-00015. [DOI] [PubMed] [Google Scholar]
  21. Brookhart M.A., Schneeweiss S., Rothman K.J., Glynn R.J., Avorn J., Stürmer T. Variable selection for propensity score models. American Journal of Epidemiology. 2006;163:1149–1156. doi: 10.1093/aje/kwj149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Cochran W.G. The planning of observational studies of human populations (with discussion) Journal of the Royal Statistical Society, Series A. 1965;128:134–155. [Google Scholar]
  23. Cochran W.G. The effectiveness of adjustment by subclassification in removing bias in observational studies. Biometrics. 1968;24:295–313. [PubMed] [Google Scholar]
  24. Cochran W.G., Rubin D.B. Controlling bias in observational studies: A review. The Indian Journal of Statistics, Series A. 1973;35:417–466. [Google Scholar]
  25. D'Agostino R.B., Jr. Propensity score methods for bias reduction in the comparison of a treatment to a non-randomized control group. Statistics in Medicine. 1998;17:2265–2281. doi: 10.1002/(sici)1097-0258(19981015)17:19<2265::aid-sim918>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
  26. Faries D.E., Leon A.C., Maria Haro J., Obenchain R.L. Analysis of observational health care data using SAS®. Cary, NC: SAS Institute Inc.; 2010. [Google Scholar]
  27. Flury B.K., Riedwyl H. Standard distance in univariate and multivariate analysis. The American Statistician. 1986;40:249–251. [Google Scholar]
  28. Gail M.H., Wieand S., Piantadosi S. Biased estimates of treatment effect in randomized experiments with nonlinear regressions and omitted covariates. Biometrika. 1984;7:431–444. [Google Scholar]
  29. Greenland S. Interpretation and choice of effect measures in epidemiologic analyses. American Journal of Epidemiology. 1987;125:761–768. doi: 10.1093/oxfordjournals.aje.a114593. [DOI] [PubMed] [Google Scholar]
  30. Greenland S., Pearl J., Robins J.M. Causal diagrams for epidemiologic research. Epidemiology. 1999;10:37–48. [PubMed] [Google Scholar]
  31. Gu X.S., Rosenbaum P.R. Comparison of multivariate matching methods: Structures, distances, and algorithms. Journal of Computational and Graphical Statistics. 1993;2:405–420. [Google Scholar]
  32. Guo S., Fraser M.W. Propensity score analysis: Statistical methods and applications. Thousand Oaks, CA: Sage; 2009. [Google Scholar]
  33. Hansen B.B. Full matching in an observational study of coaching for the SAT. Journal of the American Statistical Association. 2004;99:609–618. [Google Scholar]
  34. Hansen B.B., Klopfer S.O. Optimal full matching and related designs via network flows. Journal of Computational and Graphical Statistics. 2006;15:609–627. [Google Scholar]
  35. Hernan M.A., Brumback B., Robins J.M. Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology. 2000;11:561–570. doi: 10.1097/00001648-200009000-00012. [DOI] [PubMed] [Google Scholar]
  36. Hernan M.A., Brumback B., Robins J.M. Estimating the causal effect of zidovudine on CD4 count with a marginal structural model for repeated measures. Statistics in Medicine. 2002;21:1689–1709. doi: 10.1002/sim.1144. [DOI] [PubMed] [Google Scholar]
  37. Hill J., Reiter J.P. Interval estimation for treatment effects using propensity score matching. Statistics in Medicine. 2006;25:2230–2256. doi: 10.1002/sim.2277. [DOI] [PubMed] [Google Scholar]
  38. Ho D.E., Imai K., King G., Stuart E.A. Matching as nonparametric preprocessing for reducing model dependence in parametric causal inference. Political Analysis. 2007;15:199–236. [Google Scholar]
  39. Ho D.E., Imai K., King G., Stuart E.A. MatchIt: Nonparametric preprocessing for parametric causal inference. Journal of Statistical Software. 2011;42(8) [Google Scholar]
  40. Hong J., Yu B. Effects of kindergarten retention on children's social-emotional development: An application of propensity score method to multivariate, multilevel data. Developmental Psychology. 2008;44:407–421. doi: 10.1037/0012-1649.44.2.407. [DOI] [PubMed] [Google Scholar]
  41. Huppler Hullsiek K., Louis T.A. Propensity score modeling strategies for the causal analysis of observational data. Biostatistics. 2002;3:179–193. doi: 10.1093/biostatistics/3.2.179. [DOI] [PubMed] [Google Scholar]
  42. Imai K., King G., Stuart E.A. Misunderstandings between experimentalists and observationalists about causal inference. Journal of the Royal Statistical Society, Series A. 2008;171:481–501. [Google Scholar]
  43. Imbens G.W. Nonparametric estimation of average treatment effects under exogeneity: A review. The Review of Economics and Statistics. 2004;86:4–29. [Google Scholar]
  44. Joffe M.M., Ten Have T.R., Feldman H.I., Kimmel S.E. Model selection, confounder control, and marginal structural models: Review and new applications. The American Statistician. 2004;58:272–279. [Google Scholar]
  45. Kurth T., Walker A.M., Glynn R.J., Chan K.A., Gaziano J.M., Berger K., Robins J.M. Results of multivariable logistic regression, propensity matching, propensity adjustment, and propensity-based weighting under conditions of nonuniform effect. American Journal of Epidemiology. 2006;163:262–270. doi: 10.1093/aje/kwj047. [DOI] [PubMed] [Google Scholar]
  46. Lee B.K., Lessler J., Stuart E.A. Improving propensity score weighting using machine learning. Statistics in Medicine. 2010;29:337–346. doi: 10.1002/sim.3782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Luellen J.K., Shadish W.R., Clark M.H. Propensity scores: An introduction and experimental test. Evaluation Review. 2005;29:530–558. doi: 10.1177/0193841X05275596. [DOI] [PubMed] [Google Scholar]
  48. Lunceford J.K., Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: A comparative study. Statistics in Medicine. 2004;23:2937–2960. doi: 10.1002/sim.1903. [DOI] [PubMed] [Google Scholar]
  49. McCaffrey D.F., Ridgeway G., Morral A.R. Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychological Methods. 2004;9:403–425. doi: 10.1037/1082-989X.9.4.403. [DOI] [PubMed] [Google Scholar]
  50. Ming K., Rosenbaum P.R. Substantial gains in bias reduction from matching with a variable number of controls. Biometrics. 2000;56:118–124. doi: 10.1111/j.0006-341x.2000.00118.x. [DOI] [PubMed] [Google Scholar]
  51. Morgan S.L., Todd J.L. A diagnostic routine for the detection of consequential heterogeneity of causal effects. Sociological Methodology. 2008;38:231–281. [Google Scholar]
  52. Morgan S.L., Winship C. Counterfactuals and causal inference: Methods and principles for social research. New York, NY: Cambridge University Press; 2007. [Google Scholar]
  53. Normand S.L. T., Landrum M.B., Guadagnoli E., Ayanian J.Z., Ryan T.J., Cleary P.D., McNeil B.J. Validating recommendations for coronary angiography following an acute myocardial infarction in the elderly: A matched analysis using propensity scores. Journal of Clinical Epidemiology. 2001;54:387–398. doi: 10.1016/s0895-4356(00)00321-8. [DOI] [PubMed] [Google Scholar]
  54. Peduzzi P., Concato J., Feinstein A.R., Holford T.R. Importance of events per independent variable in proportional hazards regression analysis: II. Accuracy and precision of regression estimates. Journal of Clinical Epidemiology. 1995;48:1503–1510. doi: 10.1016/0895-4356(95)00048-8. [DOI] [PubMed] [Google Scholar]
  55. Peduzzi P., Concato J., Kemper E., Holford T.R., Feinstein A.R. A simulation study of the number of events per variable in logistic regression analysis. Journal of Clinical Epidemiology. 1996;49:1373–1379. doi: 10.1016/s0895-4356(96)00236-3. [DOI] [PubMed] [Google Scholar]
  56. Robins J.M., Hernan M.A., Brumback B. Marginal structural models and causal inference in Epidemiology. Epidemiology. 2000;11:550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
  57. Rosenbaum P.R. Model-based direct adjustment. The Journal of the American Statistician. 1987a;82:387–394. [Google Scholar]
  58. Rosenbaum P.R. The role of a second control group in an observational study. Statistical Science. 1987b;2:292–316. [Google Scholar]
  59. Rosenbaum P.R. A characterization of optimal designs for observational studies. Journal of the Royal Statistical Society, Series B. 1991;53:597–610. [Google Scholar]
  60. Rosenbaum P.R. Observational studies. 2nd ed. New York, NY: Springer-Verlag; 2002. [Google Scholar]
  61. Rosenbaum P.R. Propensity score. In: Armitage P., Colton T., editors. Encyclopedia of biostatistics. 2nd ed. Boston, MA: Wiley; 2005. pp. 4267–4272. [Google Scholar]
  62. Rosenbaum P.R. Design of observational studies. New York, NY: Springer-Verlag; 2010. [Google Scholar]
  63. Rosenbaum P.R., Rubin D.B. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983a;70:41–55. [Google Scholar]
  64. Rosenbaum P.R., Rubin D.B. Assessing sensitivity to an unobserved binary covariate in an observational study with binary outcome. Journal of the Royal Statistical Society, Series B. 1983b;45:212–218. [Google Scholar]
  65. Rosenbaum P.R., Rubin D.B. Reducing bias in observational studies using subclassification on the propensity score. Journal of the American Statistical Association. 1984;79:516–524. [Google Scholar]
  66. Rosenbaum P.R., Rubin D.B. Constructing a control group using multivariate matched sampling methods that incorporate the propensity score. The American Statistician. 1985;39:33–38. [Google Scholar]
  67. Rubin D. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
  68. Rubin D.B. Estimating causal effects from large data sets using propensity scores. Annals of Internal Medicine. 1997;127:757–763. doi: 10.7326/0003-4819-127-8_part_2-199710151-00064. [DOI] [PubMed] [Google Scholar]
  69. Rubin D.B. Using propensity scores to help design observational studies: Application to the tobacco litigation. Health Services & Outcomes Research Methodology. 2001;2:169–188. [Google Scholar]
  70. Rubin D.B. On principles for modeling propensity scores in medical research. Pharmacoepidemiology Drug Safety. 2004;13:855–857. doi: 10.1002/pds.968. [DOI] [PubMed] [Google Scholar]
  71. Rubin D.B. Matched sampling for causal effects. New York, NY: Cambridge University Press; 2006. [Google Scholar]
  72. Rubin D.B. The design versus the analysis of observational studies for causal effects: Parallels with the design of randomized trials. Statistics in Medicine. 2007;26:20–36. doi: 10.1002/sim.2739. [DOI] [PubMed] [Google Scholar]
  73. Rubin D.B., Thomas N. Combining propensity score matching with additional adjustments for prognostic covariates. Journal of the American Statistical Association. 2000;95:573–585. [Google Scholar]
  74. Schafer J.L., Kang J. Average causal effects from nonrandomized studies: A practical guide and simulated example. Psychological Methods. 2008;13:279–313. doi: 10.1037/a0014268. [DOI] [PubMed] [Google Scholar]
  75. Sekhon J.S. Multivariate and propensity score matching software with automated balance optimization: The Matching package for R, Journal of Statistical Software. in press. [Google Scholar]
  76. Setoguchi S., Schneeweiss S., Brookhart M.A., Glynn R.J., Cook E.F. Evaluating uses of data mining techniques in propensity score estimation: A simulation study. Pharmacoepidemiology and Drug Safety. 2008;17:546–555. doi: 10.1002/pds.1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Shah B.R., Laupacis A., Hux J.E., Austin P.C. Propensity score methods give similar results to traditional regression modeling in observational studies: A systematic review. Journal of Clinical Epidemiology. 2005;58:550–559. doi: 10.1016/j.jclinepi.2004.10.016. [DOI] [PubMed] [Google Scholar]
  78. Staff J., Patrick M.E., Loken E., Maggs J.L. Teenage alcohol use and educational attainment. Journal of Studies on Alcohol and Drugs. 2008;69:848–858. doi: 10.15288/jsad.2008.69.848. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Steyerberg E.W. Clinical prediction models: A practical approach to development, validation, and updating. New York, NY: Springer; 2009. [Google Scholar]
  80. Stürmer T., Joshi M., Glynn R.J., Avorn J., Rothman K.J., Schneeweiss S. A review of the application of propensity score methods yielded increasing use, advantages in specific settings, but not substantially different estimates compared with conventional multivariable methods. Journal of Clinical Epidemiology. 2006;59:437–447. doi: 10.1016/j.jclinepi.2005.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Weitzen S., Lapane K.L., Toledano A.Y., Hume A.L., Mor V. Weaknesses of goodness-of-fit tests for evaluating propensity score models: The case of the omitted confounder. Pharmacoepidemiolgy and Drug Safety. 2005;14:227–238. doi: 10.1002/pds.986. [DOI] [PubMed] [Google Scholar]
  82. Wyse A.E., Keesler V., Schneider B. Assessing the effects of small school size on mathematics achievement: A propensity score-matching approach. Teachers College Record. 2008;110:1879–1900. [Google Scholar]
  83. Ye Y., Kaskutas L.A. Using propensity scores to adjust for selection bias when assessing the effectiveness of Alcoholics Anonymous in observational studies. Drug and Alcohol Dependence. 2009;104:56–64. doi: 10.1016/j.drugalcdep.2009.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Multivariate Behavioral Research are provided here courtesy of Taylor & Francis

RESOURCES