Abstract
There are many sources of systematic variation in cDNA microarray experiments which affect the measured gene expression levels (e.g. differences in labeling efficiency between the two fluorescent dyes). The term normalization refers to the process of removing such variation. A constant adjustment is often used to force the distribution of the intensity log ratios to have a median of zero for each slide. However, such global normalization approaches are not adequate in situations where dye biases can depend on spot overall intensity and/or spatial location within the array. This article proposes normalization methods that are based on robust local regression and account for intensity and spatial dependence in dye biases for different types of cDNA microarray experiments. The selection of appropriate controls for normalization is discussed and a novel set of controls (microarray sample pool, MSP) is introduced to aid in intensity-dependent normalization. Lastly, to allow for comparisons of expression levels across slides, a robust method based on maximum likelihood estimation is proposed to adjust for scale differences among slides.
INTRODUCTION
DNA microarrays are part of a new class of biotechnologies that allow the monitoring of expression levels in cells for thousands of genes simultaneously. In a typical microarray experiment utilizing ‘spotted arrays’, the two mRNA samples to be compared are reverse transcribed into cDNA, labeled using two different fluorophores (usually a red fluorescent dye, Cy5, and a green fluorescent dye, Cy3) and then hybridized simultaneously to the glass slide. Intensity values generated from hybridization to individual DNA spots are indicative of gene expression levels, and comparisons in gene expression levels between the two samples are derived from the resulting intensity ratios (1). Applications of microarrays range from the study of gene expression in yeast under different environmental stress conditions (2,3) to the comparison of gene expression profiles for tumors from cancer patients (4–9).
In order to accurately and precisely measure gene expression changes, it is important to take into account the random (experimental) and systematic variations that occur in every microarray experiment. For example, a well-known source of systematic variation arises from biases associated with the different fluorescent dyes. This can most easily be seen in an experiment where two identical mRNA samples are labeled with different dyes and subsequently hybridized to the same slide (10). In this instance, it is rare to have the dye intensities equal across all spots between the two samples. Even though such systematic biases may be comparatively small, they may be confounding when searching for subtle biological differences. Dye biases can stem from a variety of factors, including physical properties of the dyes (heat and light sensitivity, relative half-life), efficiency of dye incorporation, experimental variability in hybridization and processing procedures, or scanner settings at the data collection step. Furthermore, the relative gene expression levels from replicate experiments may have different sample variances due to differences in experimental conditions. Many of these factors, whether internal or external to the target samples, make distinctions between differentially and constantly expressed genes difficult [in this article we adopt the definitions of ‘probe’ and ‘target’ from the January 1999 supplement to Nature Genetics (11), whereby the term target refers to the samples hybridized to the array and the term probe refers to the DNA sequences spotted on the array].
The purpose of normalization is to minimize systematic variations in the measured gene expression levels of two co-hybridized mRNA samples, so that biological differences can be more easily distinguished, as well as to allow the comparison of expression levels across slides. Current methods of normalization fail to account for important sources of systematic variation (e.g. intensity- or spatially-dependent dye biases). In this article we propose a composite normalization procedure, based on robust local regression, to accommodate different types of dye biases and the use of control sequences spotted on the array. The selection of a suitable set of control spots for use in the normalization procedure is critical for proper normalization. To this end, we introduce a novel control sample (microarray sample pool, MSP), with minimal sample-specific bias over a large intensity range, and show that it is effective in many types of microarray experiments.
MATERIALS AND METHODS
Biological samples
Preparation of RNA samples and microarray analysis. Tissues were dissected, solubilized in Trizol (Gibco BRL) and total RNA was prepared according to the manufacturer’s suggested protocol. Prior to reverse transcription and labeling, total RNA samples were treated with DNase using RQ RNase-free DNase (Promega) for 20 min at 37°C. RNA samples were reverse transcribed and labeled for microarray analysis using standard techniques (6,12). Briefly, RNA samples were reverse transcribed with Superscript II reverse transcriptase in the presence of 2-aminoallyl-dUTP. Samples were purified and coupled to Cy3 or Cy5 as described (6,12,13). Labeled targets were resuspended in hybridization buffer and applied to glass microarrays. Hybridizations were performed overnight at 50–55°C. Washed and dried slides were imaged in an Axon GenePix 4000A scanner.
Experiment A: apolipoprotein AI (apo AI) experiment. The treatment group consisted of eight mice with the apo AI gene knocked out and the control group consisted of eight control C57Bl/6 mice. For each of these 16 mice, target cDNA was obtained from mRNA by reverse transcription and labeled using a red fluorescent dye, Cy5. The reference sample used in all hybridizations was prepared by pooling cDNA from the eight control mice and was labeled with a green fluorescent dye, Cy3. Target cDNA was hybridized to microarrays containing 6384 cDNA probes, which included 257 genes thought to be related to lipid metabolism. Probes were spotted onto the glass slides using a 4 × 4 print head and each of the corresponding 16 print tip groups was laid out in a 19 × 21 array or sub-grid. For further details the reader is referred to Callow et al. (14).
Experiment B: olfactory bulb experiment. In this experiment, comparisons were made between different spatial regions of the mouse olfactory bulb to screen for possible region-specific differences in gene expression (D.M.Lin, Y.H.Yang, J.Scolnick, L.Brunet, V.Peng, T.Speed and J.Ngai, submitted for publication). The target cDNA was hybridized to glass microarrays containing ∼18 000 isolated expressed sequence tags (ESTs) from the RIKEN Release 1 mouse cDNA library (15). The olfactory bulb is an ellipsoidal structure, so in order to make a 3-dimensional representation using binary comparisons, bulbs were separately sub-dissected into three sections along each of the three orthogonal axes. RNA was collected from a number of different mice and samples from the same anatomical domains were harvested and pooled (D.M.Lin, Y.H.Yang, J.Scolnick, L.Brunet, V.Peng, T.Speed and J.Ngai, submitted for publication). Comparisons were made between maximally separated regions: anterior versus posterior, medial versus lateral and dorsal versus ventral regions.
MSP titration series. Total EST collections were generated from amplification of PCR products for microarray fabrication. Samples corresponding to all 18 816 ESTs from the RIKEN Release 1 cDNA library were pooled and precipitated. An MSP was also made from a randomly picked non-normalized plasmid library generated from mouse cerebellum (A.Finn and T.Serafini, unpublished results). Precipitated samples were resuspended and serially diluted in preparation for printing. Six steps were used in the dilution series and the samples were then spotted in the middle of the first or last row of each of the print tip groups. Microarrays were prepared as discussed previously (6).
Image processing
Each hybridization produced a pair of 16-bit images, which were processed using the software package Spot (16). The main quantities of interest produced by the image analysis methods (segmentation and background correction) are the (R,G) fluorescence intensity pairs for each gene on each array (where R = red for Cy5 and G = green for Cy3). Note that we call the spotted DNA sequences ‘genes’, whether they correspond to actual genes, ESTs or DNA sequences from other sources.
Statistical methods
An ‘MA-plot’, as described in Dudoit et al. (10), is used to represent the (R,G) data, where M = log2R/G and A = log2√(R × G). We have found MA-plots to be helpful in terms of identifying spot artifacts and detecting intensity-dependent patterns in the log ratios M. They are also very useful for the purpose of normalization, as illustrated next with several location normalization procedures. Within-slide normalization for location consists of subtracting a function c(.) from individual intensity log ratios, where the function c(.) is computed separately for each slide, using only data from that hybridization.
Global normalization. Global methods assume that the red and green intensities are related by a constant factor, i.e. R = kG, and the center of the distribution of log ratios is shifted to zero
log2R/G → log2R/G – c = log2R/(kG)
A common choice for the location parameter c = log2k is the median or mean of the intensity log ratios M for a particular gene set.
Intensity-dependent normalization. We use the robust scatter plot smoother ‘lowess’, implemented in the statistical software package R (17), to perform a local A-dependent normalization
log2R/G → log2R/G – c(A) = log2R/[k(A)G]
where c(A) is the lowess fit to the MA-plot. The lowess scatter plot smoother performs robust locally linear fits. In particular, it will not be affected by a small percentage of differentially expressed genes, which will appear as outliers in the MA-plot. The user-defined parameter f is the fraction of the data used for smoothing at each point; the larger the f value, the smoother the fit. We typically use f = 40%.
Within-print tip group normalization. Within-print tip group normalization is simply a (print tip + A)-dependent normalization, i.e.
log2R/G → log2R/G – ci(A) = log2R/[ki(A)G]
where ci(A) is the lowess fit to the MA-plot for the ith grid only (i.e. for the ith print tip group), i = 1, ..., I, and I denotes the number of print tips.
Scale normalization. Starting from data which have been location normalized as just described, we suppose that the log ratios from the ith print tip group follow a normal distribution with mean zero and variance ai2σ2, where σ2 is the variance of the true log ratios and ai2 is the scale factor for the ith print tip group. In order to perform scale normalization, the scale factors ai for the different print tip groups are estimated and then eliminated. Enforcing the natural constraint ∑Ii = 1logai2 = 0, with I denoting the total number of print tip groups on the array (or the number of slides, for multiple slide normalization discussed below), the maximum likelihood estimate for ai is
![]() i2 = (∑nij = 1Mij2)/[I√(ΠIk = 1∑nkj = 1Mkj2)]
i2 = (∑nij = 1Mij2)/[I√(ΠIk = 1∑nkj = 1Mkj2)]
where Mij denotes the jth log ratio in the ith print tip group, j = 1, ..., ni. A robust alternative to this estimate, which we find preferable, is
where the median absolute deviation MAD is defined by
MADi = medianj{½Mij – medianj(Mij) ½}
Composite normalization. For a given print tip group the composite normalization curve is a weighted average of the MSP lowess curve and the lowess curve based on all genes in the print tip group. The weights are dependent on the cumulative number of genes at different intensity levels A. An outline of this procedure for a spot in the ith print tip group is as follows. (i) Estimate ![]() i(A), the lowess fit to the MA-plot for the ith print tip group. (ii) Estimate
i(A), the lowess fit to the MA-plot for the ith print tip group. (ii) Estimate ![]() (A), the lowess fit to the MA-plot using only spots from the MSP titration series. (iii) Calculate the weighted average, ci(A) = αA
(A), the lowess fit to the MA-plot using only spots from the MSP titration series. (iii) Calculate the weighted average, ci(A) = αA ![]() (A) + (1 – αA)
(A) + (1 – αA) ![]() i(A), where αA is defined as the proportion of genes less than a given intensity A.
i(A), where αA is defined as the proportion of genes less than a given intensity A.
Comparison between different normalization methods. After image processing and normalization, the gene expression data can be summarized by a matrix X of intensity log ratios M = log2R/G, with p rows corresponding to the genes being studied and n columns corresponding to the different hybridizations. In the apo AI experiment p = 6384 and there were n1 = 8 control (C57Bl/6 mice) and n2 = 8 treatment (apo AI knockout mice) hybridizations. Differentially expressed genes were identified by computing two-sample Welch t-statistics. For gene j the t-statistic comparing gene expression in the control and treatment groups is
tj = (x2j – x1j)/√[(s1j2/n1) + (s2j2/n2)]
where `x1j and `x2j denote the average background-corrected and normalized expression level of gene j in the eight control and eight treatment hybridizations, respectively. Similarly, s1j2 and s2j2 denote the variances of gene j expression level in the control and treatment hybridizations, respectively. Large absolute t-statistics suggest that the corresponding genes have different expression levels in the control and treatment groups. The statistical significance of the results was assessed based on P-values adjusted for multiple comparisons. These adjusted P-values were estimated by permutation, using Westfall and Young’s step-down adjusted P-value procedure in algorithm 4.1 (18). The analysis of the apo AI experiment is described in detail in Dudoit et al. (10).
In order to compare the different within-slide normalization procedures, we considered their effect on the location and scale of the log ratios M using box plots. A Gaussian kernel density estimator (the ‘density’ function from the statistical software package R, bandwidth size 0.17) is also used to produce density plots of the log ratios for each of the normalization methods. For experiment A we considered the effect of the normalization procedures on the t-statistics for the knockout gene.
RESULTS
Within-slide normalization: intensity- and spatially-dependent systematic error
We first address within-slide normalization, i.e. normalization issues associated with data obtained from a single slide. A well-known source of error can be attributed to biases linked to the different dyes used at the labeling step. Current methods of global normalization assume a uniform grading of systematic error across all variables in an experiment. Two major assumptions are usually made: (i) all cDNA species within a sample will incorporate an equivalent amount of dye per mole cDNA; (ii) there are no other variables (e.g. spatial location, overall intensity, plate) that contribute to dye biases across the slide. These assumptions are too simplistic to account for the multiple sources of systematic error typically encountered in microarray experiments. The problem is best illustrated in an experiment where identical mRNA samples are labeled with Cy3 and Cy5 and subsequently hybridized to the same slide [self–self comparison; described in Dudoit et al. (10)]. In a ‘perfect’ self–self hybridization the intensity log ratios M in an MA-plot should be evenly distributed around zero across all intensity values A. However, this is rarely the case, and systematic error often manifests itself in terms of non-zero log ratios M. Furthermore, the imbalance in the red and green intensities is usually not constant across the spots and can vary according to overall spot intensity A (indicated by a curvature in the MA-plot), location on the array, plate origin and possibly other variables.
Intensity-dependent dye bias can be seen in the apo AI experiment (14). Apo AI is a gene known to play a pivotal role in high-density lipoprotein metabolism. The goal of the experiment was to identify genes with altered expression in the livers of mice with the apo AI gene knocked out compared with inbred C57Bl/6 control mice. In this instance, it was found that the vast majority of genes examined on the microarray showed no difference in expression level. The clear curvature in the MA-plot in Figure 1A strongly suggests the existence of an intensity-dependent dye bias.
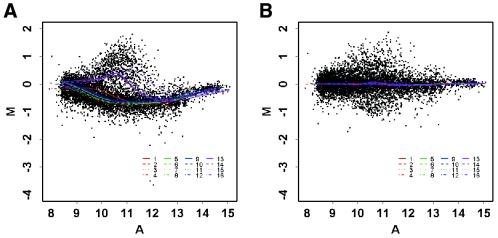
Figure 1.
Within-slide normalization. (A) MA-plot demonstrating the need for within-print tip group location normalization. (B) MA-plot after within-print tip group location normalization. Both panels display the lowess fits (f = 40%) for each of the 16 print tip groups (data from apo AI knockout mouse number 8 in experiment A).
Some systematic differences may exist between the print tips, such as slight differences in the length or in the opening of the tips, and deformation after many hours of printing. We therefore also performed individual lowess fits within each print tip group. The arrays in the apo AI experiment were printed with a 4 × 4 print head, so each lowess fit in Figure 1 corresponds to spots printed with a single print tip. Four within-print tip group lowess curves stand out from the remaining 12 curves, indicating strong print tip or spatial effects. These four curves correspond to the last row of print tips in the 4 × 4 print head (print tips 13–16). This pattern was visible in the raw images, where the bottom four grids tended to have a higher red signal. We further examined the spatial effects by considering box plots of the log ratios M for each print tip group. Figure 2 shows that print tip groups 13–16 have a larger spread in their log ratios than any of the other 12 print tip groups. Such a difference in spread may result in misidentification of genes that are differentially expressed in the knockout mice compared to the control mice. Thus, normalization for scale across print tip groups seems desirable here.
Figure 2.
Within-slide normalization: box plots displaying the intensity log ratio distribution, for each of the 16 print tip groups before and after different normalization procedures. The array was printed using a 4 × 4 print head and the print tip groups are numbered first from left to right, then from top to bottom, starting from the top left corner (data from apo AI knockout mouse number 8 in experiment A). (A) Before normalization. (B) After within-print tip group location normalization, but before scale adjustment. (C) After within-print tip group location and scale normalization.
Within-slide normalization using the majority of genes on the microarray
For the apo AI experiment considered in Figures 1 and 2, global normalization, in which a constant adjustment is used to force the distribution of the log ratios to have a median zero within each slide, would result in a vertical translation of the MA-plot. It would not correct for intensity- or spatially-dependent effects, including local differences in the spread of the log ratios M. As a first pass towards eliminating intensity and spatial biases, we considered a normalization procedure in which the majority of genes on the array are used for normalization. This is a reasonable assumption when there are good reasons to expect that (i) only a relatively small proportion of the genes will vary significantly in expression between the two co-hybridized mRNA samples or (ii) there is symmetry in the expression levels of the up/down-regulated genes. The data shown in Figures 1 and 2 are good examples of this situation.
To address both intensity and spatial normalization issues, we first incorporated an intensity modifier into our normalization procedures. We used the scatter plot smoother lowess to produce robust location estimates of the intensity log ratios M for various intensity levels A and to adjust each gene with a different normalization value depending on its overall intensity. Other variables that may contribute to systematic bias include differences in print tips and spatial location. Because every grid in an array is printed using the same print tip, print tip groups can also be used as proxies for spatial effects on the slide. Thus, we also incorporated a print tip modifier into the intensity-dependent normalization. It might be thought that the layout of genes on the slide could lead to one or more print tip groups being enriched for differentially expressed genes and, hence, invalidate the assumption underlying print tip group normalization. While we cannot rule out chance imbalances in the spatial distribution of differentially expressed genes, the mechanics of spotting cDNA onto the slide makes a large effect of this kind unlikely. Even if one had a collection of genes known or expected to be differentially expressed in one or more microtiter plates, they would be spotted evenly across the slide by the printer.
In principle, after within-print tip group location normalization, the log ratios from the different print tip groups should be centered around zero (Fig. 2B). However, it is possible that the log ratios from the various print tip groups have different spreads; if this is the case, a scale adjustment may be required. Figure 2 displays box plots of the intensity log ratios M for a slide in experiment A, before normalization (Fig. 2A), after within-print tip group location normalization (Fig. 2B) and after within-print tip group location and scale normalization (Fig. 2C). In Figure 2B there is a disproportionately large number of extreme log ratios in the lower four grids. After scale normalization, the extreme log ratios are evenly distributed on the array (Fig. 2C). Again, this procedure assumes that a relatively small proportion of the genes vary significantly in expression between the two co-hybridized mRNA samples, as would be expected when comparing samples from wild-type mice versus mice harboring a mutation in a single gene. In addition, it is assumed that the spread of the distribution of the log ratios should be roughly the same for all print tip groups. The robust statistic MAD, like the robust lowess smoother, will not be affected by a small percentage of differentially expressed genes, which will appear as outliers in the MA-plots.
In another example of within-slide location normalization, Figure 3 shows an MA-plot from experiment B, for a comparison of mRNA levels in the anterior and posterior portions of the mouse olfactory bulb. These mRNA samples are biologically very similar and very few genes are expected to be differentially expressed. Indeed, the MA-plot shows very little divergence from the lowess fit to all genes and the scatter plot is roughly symmetrical about the lowess curve. We thus performed a print tip group normalization using all genes. Figure 3 displays the intensity data before (Fig. 3, left) and after normalization (Fig. 3, right). The normalization procedure resulted in a scatter plot centered around an M value of zero across the A intensity range, thus indicating that the types of systematic errors we have identified have been minimized.
Figure 3.
Within-slide normalization: MA-plot for comparison of the anterior versus posterior portion of the olfactory bulb. These samples are very similar and we do not expect many genes to change. The cyan dots represent the MSP titration series and the cyan curve represents the corresponding lowess fit. The red curve corresponds to the lowess fit for the entire dataset. Control genes are highlighted in yellow (tubulin and GAPDH), green (mouse genomic DNA) and orange (an approximate rank-invariant set of genes with P = 0.01 and l = 25). (Left) MA-plot before normalization. (Right) MA-plot after within-print tip group location normalization.
Within-slide normalization using MSP
Frequently, the expression profiles in biological samples are more divergent in nature than in the examples investigated above. Thus, normalization based upon all genes may be inaccurate. A control sample that spans the intensity range and exhibits a relatively constant expression level across biological samples is desirable. Yeast genomic DNA has been used for normalization in that system. Since all species within an mRNA sample can hybridize to this control, sample-specific bias is reduced. The genomic DNA approach does not, however, directly extend to more complex metazoan systems, where the high ratio of non-coding to coding DNA effectively reduces the signal from such a control below the detection threshold in a microarray experiment.
We therefore constructed a novel control sample ensemble, MSP, inclusive of all genes present on the microarray. This sample should be analogous to genomic DNA without the intervening sequences and, thus, provides a potential probe for every species within a labeled cDNA target. We titrated this sample over the intensity range of a typical microarray experiment in order to account for all levels of intensity-dependent bias. The utility of this control is demonstrated in Figure 3, which highlights the MSP titration series (cyan dots) and the corresponding lowess fit to the MSP spots (cyan curve). Notice that the MSP curve is the same as the lowess fit to the MA-plot based on all genes (red curve). An intensity-dependent normalization using the MSP control as a reference would thus be similar, in this case, to that using all genes.
In experiment B we made a more divergent comparison between mRNA samples from the medial and lateral portions of the olfactory bulb. Due to the presence of vascular tissue near the medial bulb, medial samples have a higher representation of blood tissue. Figure 4A displays the MA-plot for the medial versus lateral comparison. The genetic divergence between the samples is evident in the increased spread of the log ratios, particularly in the high intensity range. The lowess curve based on all genes (red) and the lowess curve based on the MSP titration series (cyan) are different at high intensity values. In such a case, where samples are widely divergent at high intensities, normalization based on the MSP titration series appears to be more accurate. However, whereas the MSP spots produce more accurate estimates of expression levels, these estimates may be less stable in the context of spatial normalization, due to the small number of MSP spots per print tip group.
Figure 4.
Within-slide normalization: MA-plot for comparison of the medial versus lateral portion of the olfactory bulb. The cyan dots represent the MSP titration series and the cyan curve represents the corresponding lowess fit. The red curve corresponds to the lowess fit for the entire dataset. The green curve represents the composite normalization curve. Control genes are highlighted in yellow (tubulin and GAPDH), green (mouse genomic DNA) and orange (an approximate rank-invariant set of genes). (A) MA-plot before normalization. (B) MA-plot after composite normalization.
Comparisons of MSP to other control samples
In some instances a small number of known genes, for example housekeeping genes whose expression is expected to be constant across samples, are utilized for microarray normalization. Such genes are often highly expressed, as illustrated in Figure 3 for tubulin and glyceraldehyde-3-phosphate dehydrogenase (GAPDH) (yellow). Typically, housekeeping genes are not representative of all intensity values A and are therefore limited in their utility for intensity-dependent normalization. In addition, there is a sample-specific bias for many genes which may not be predictable; this is again non-ideal for use as a control.
Another approach is to select a rank-invariant set of genes. A set of genes is said to be rank-invariant if their ranks are the same for the red and green intensities. In practice, a maximal invariant set tends to be too small and an iterative procedure for finding an approximately invariant set of genes has been proposed (19,20). These genes are highlighted in orange in Figure 3 and were obtained using the method described in Tseng et al. (20) with P = 0.01 and l = 25. The value P is chosen such that a conserved set of genes is selected. Notice that this set of spots overlaps the lowess fit to the MA-plot based on all genes.
Composite within-slide normalization
We propose a composite normalization method to address the limitations of using all genes or only the MSP titration series for normalization. The composite normalization curve is a weighted average of the MSP curve and the within-print tip group lowess curve based on all genes. The weights are dependent on the cumulative number of genes at different intensity levels. Figure 4B shows the MA-plot after within-print tip group normalization. In this figure the green composite normalization curve is a weighted average of the red and cyan colored curves. Note that the divergence of the red from the green curve at high intensity values still persists after normalization. In practice, we find composite normalization necessary in the case of divergent samples. Biologically significant outliers in experiment B were more consistently identified when composite normalization was incorporated in the analysis (data not shown).
Comparison between different normalization methods
In order to compare the different within-slide normalization methods, we considered their effect on the location and scale of the log ratios M. Figure 5A shows density plots of the log ratios for different normalization methods. Without normalization (black curve) the log ratios are centered around –1, indicating a bias towards the green (Cy3) dye. A global median normalization (red curve) shifts the center of the log ratio distribution to zero, but does not affect the spread. The dependence of the log ratio M on the overall intensity A is also still present (see Fig. 1). Both the intensity-dependent (green curve) and within-print tip group (blue curve) location normalization methods reduce the spread of the log ratios compared to a global normalization. A within-print tip group scale normalization (cyan curve) further reduces the spread slightly.
Figure 5.
Within-slide normalization. (A) Density plots of the log ratios M before and after different normalization procedures. The solid black curve represents the density of the log ratios before normalization. The red, green, blue and cyan curves represent the densities after global median normalization, intensity-dependent location normalization, within-print tip group location normalization and within-print tip group scale normalization, respectively (data from apo AI knockout mouse number 8 in experiment A). (B) Plot of t-statistics for different normalization methods. The numbers 1–8 represent the differentially expressed genes identified in Dudoit et al. (10) and confirmed using RT–PCR: indices 1–3 represent the three apo AI genes spotted on the array. Empty circles represent the remaining 6376 genes where no effect is expected. Only t values less than –4 are shown.
The different methods were also evaluated based on their ability to identify genes which are known to be differentially expressed. For experiment A the apo AI gene is knocked out in the eight treatment mice, so one expects the t-statistics to take on very large negative values for this gene. Figure 5B shows a truncated plot of the extreme t-statistics for each of the methods. The global median, intensity-dependent and within-print tip group location normalization methods seem to perform best in terms of their ability to detect the three copies of the knocked out apo AI gene. A good method should enable a clear distinction between differentially and constantly expressed genes as reflected by the t-statistic, i.e. one expects a large jump in the t-statistic between the least extreme of the differentially expressed genes and the most extreme of the remaining genes. The largest jump in P-values is observed for within-print tip group location normalization. Thus, in the situation presented by experiment A, where log ratios from the different arrays have fairly similar spreads (see Fig. 2), within-print tip group location normalization enables the best separation between differentially expressed genes and noise.
Multiple slide normalization
Having addressed location and scale normalization issues within a slide, all normalized log ratios should be centered around zero. However, in many experiments expression levels must be compared across different slides. It is important to note that individual slides in a multiple slide comparison may need to be adjusted for scale when the different slides have substantially different spreads in their intensity log ratios. Failing to perform a scale normalization could lead to one or more slides having undue weight when averaging log ratios across slides. We can apply the principles used for within-slide print tip group scale normalization to multiple slide scale adjustment.
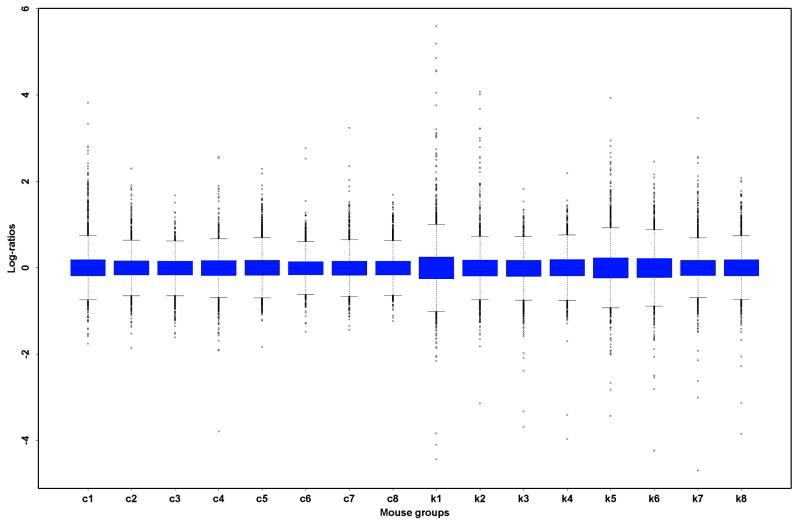
In practice, the need for scale normalization between slides will be determined empirically. Figure 6 displays box plots of the log ratios for each of the 16 slides in experiment A, after within-print tip group location and scale normalization. The box plots are centered at zero and have fairly similar spreads. In this instance we chose not to adjust for scale, as the noise introduced by a scale normalization of the different slides may be more detrimental than a small difference in scale.
Figure 6.
Multiple slide normalization: box plots displaying the intensity log ratio distribution for different slides/mice for experiment A, after within-print tip group location and scale normalization. The first eight box plots represent the data for the eight control mice and the last eight represent the data for the eight apo AI knockout mice.
DISCUSSION
Intensity data from microarray experiments are subject to a variety of random and systematic errors. This paper has introduced location and scale normalization methods for different types of cDNA microarray experiments and discussed different sets of control spots utilized in normalization. The location normalization procedure is based on robust local regression of the intensity log ratios on overall spot intensity and accounts for intensity and spatial dependence in the dye biases. A MSP titration series was constructed and used as a set of controls for normalization. The advantages of the MSP are the minimal sample-specific bias and the coverage of a wide intensity range. In addition, we have proposed a composite normalization procedure, whereby the utility of different sets of control spots and normalization methods are combined. The different normalization methods were compared using gene expression data from two experiments: the apo AI experiment (experiment A), with replicated treatment and control slides, and the mouse olfactory bulb experiment (experiment B). Normalization can be performed at three different levels: (i) within a single slide; (ii) between a pair of slides for dye-swap experiments (21); and (iii) among multiple slides.
Within-slide normalization methods
For within-slide normalization, global methods have been used as pre-processing steps in a number of papers on the identification of differentially expressed genes in single slide cDNA microarray experiments (22,23). Such procedures assume that the red and green intensities can be related by a multiplicative constant. In one of the first proposed normalization methods, Chen et al. (22) derived an iterative procedure for estimating normalization constants. Similar approaches have been implemented in widely used microarray software packages [e.g. GenePix (24)]. Kerr et al. (25) and R.D.Wolfinger, G.Gibson, E.D.Wolfinger, L.Bennett, H.Hamadeh, P.Bushel, C.Afshari and R.S.Paules (SAS Institute, unpublished data) proposed the use of ANOVA models for normalization purposes. Their methods essentially perform only a global normalization and do not correct for intensity or scale differences. We have found that the standard global median normalization can often be inadequate due to spatially- and intensity-dependent dye biases. We propose instead a within-print tip group location normalization method which is based on robust local regression of the log ratios M on overall spot intensity A (the lowess smoother for MA-plots). Compared with other normalization procedures, this approach provided a clearer distinction between the differentially and constantly expressed genes in experiment A.
Other intensity-dependent normalization methods have been proposed in recent articles. Finkelstein et al. (26) recommended an iterative linear regression procedure, which essentially amounts to robust linear regression. Sapir and Churchill (27) suggested using the orthogonal residuals from the robust regression of logR versus logG as the normalized log ratios. Since an MA-plot amounts to a 45° counterclockwise rotation of the (logG,logR) coordinate system (up to multiplicative constants), their method is similar to fitting a robust regression line through the MA-plot, instead of a lowess curve. One can view these two linear normalizations as a more constrained version of our intensity-dependent normalization. Kepler et al. (28) proposed a more general intensity-dependent normalization approach, which uses a different local regression method instead of the lowess smoother. Most methods suggested thus far do not correct for spatial biases in the log ratios. As we have shown, spatial bias is also a significant source of systematic error, due to hybridization artifacts or print tip effects during printing of the microarray. Our proposed normalization procedures correct for these artifacts.
Within-slide location normalization methods adjust the intensity log ratios M such that they are approximately zero for genes that are constantly expressed in the two co-hybridized samples. The box plots of the location normalized log ratios in each print tip group in Figure 2 suggest that some scale adjustment may also be required within slide. However, within-print tip group scale normalization seems to have decreased our ability to identify the differentially expressed genes in experiment A. We believe that this is due to an increase in the variability (the denominator of the t-statistic) of the log ratios for the eight differentially expressed genes compared to the rest of the genes.
Multiple slide normalization methods
A similar approach to that described for within-slide scale normalization may also be extended to perform scale normalization across slides. In practice, multiple slide normalization aims to adjust for different sample variances in log ratios across slides. Such adjustments are required so that the relative expression levels from one particular slide do not dominate the average relative expression levels across replicate slides. In general there is a trade-off between the gains achieved by scale normalization and the possible increase in variability introduced by this additional step. In cases where the scale differences are fairly small it may thus be preferable to perform only a location normalization. Further investigations are underway to develop an improved procedure for scale adjustment and to identify better comparison criteria to assess the effectiveness of various normalization procedures.
Comparisons of MSP to commonly used control samples
In general, the set of control spots most appropriate for normalization depends on the nature of the experiment. Traditional methods based upon intensity values of housekeeping genes often show sample-specific bias and do not address the issue of intensity-dependent dye biases. Other drawbacks include the possibility that housekeeping genes may actually be regulated within an experimental sample. Housekeeping genes also tend to be highly expressed and, hence, may not be representative of other genes of interest. It is clear that a less localized type of control is required to obtain accurate normalization. The other three types of control examined in this article were chosen for their representation of as many genes and intensity values as possible so as to minimize sample bias.
The MSP titration series was constructed with this specific aim in mind. In the yeast system, normalization is typically performed using yeast genomic DNA, which contains proportionately small amounts of non-coding DNA. In contrast, the genomes of higher organisms such as mice contain a much higher representation of non-coding DNA. The MSP is analogous to genomic DNA as a control, with the exception that non-coding regions are removed. Typically, a concentration titration is done to span as wide an intensity range as possible. However, due to limitations in the construction of the MSP, very high expression values cannot be represented. In practice, one could construct an MSP of lower complexity with a larger representation of highly expressed genes. Since most rare and low expression genes do not contribute significantly to an MSP signal, removing this population is analogous to further removal of non-coding DNA. Theoretically, all labeled cDNA sequences could hybridize to this mixed probe sample, so it is therefore minimally subject to any sample-specific bias.
The use of all genes for normalization offers the most stability in terms of estimating spatially- and intensity-dependent trends in the log ratios. However, in biological samples which show significant divergence, a lowess fit to the MA-plot based on all genes may not produce accurate normalized log ratios. In such instances, it would be more appropriate to normalize using the MSP spots alone. While the MSP and rank-invariant controls are effective for intensity-dependent normalization, we have found that normalization based on all genes is more reliable for spatial normalization . This is due in part to the low representation of MSP and rank-invariant spots per print tip group (6–12 spots per 400 spots) and is an example of bias variance trade-off.
Composite normalization and the MSP titration series
This article has proposed a composite normalization procedure which combines the utility of normalization methods based on all genes and those based on only the MSP titration spots. For low A intensity values, normalization is based on all genes in the corresponding intensity range. For higher A values, particularly in more divergent biological samples, normalization is based primarily on the MSP titration series. In other circumstances as they warrant, other normalization methods may be incorporated into the composite technique. For example, in cases where microarrays are printed without MSP titration spots, very high intensities may be normalized using housekeeping genes and median to low intensities may be normalized using all genes in the corresponding range.
The MSP spots were essential to validate the assumptions behind our various normalization procedures and are necessary for normalizing biologically divergent samples. The construction of the MSP titration series is important, as we observed intensity-dependent dye biases in many experiments. Efforts are still in progress to devise variants of this control set for scale normalization procedures. It is evident that no single control sample or normalization procedure is accurate or adequate for all types of microarray comparisons. However, it is becoming increasingly common for investigators to print microarrays with a large complement of control spots. This flexibility expands the opportunity to customize normalization procedures, depending on the experimental conditions.
The strengths and weaknesses of the normalization techniques and control samples discussed in this paper are summarized in Table 1. Finally, the methods described in the article are implemented in the package R (17), SMA (Statistics for Microarray Analysis), which may be downloaded from http://www.R-project.org. Supplementary analyses, figures and datasets are available at http://www.stat.berkeley.edu/users/terry/zarray/Html/index.html.
Table 1. The various normalization methods considered in this article.
| |
|
Within-slide | Multiple slide |
|||
|---|---|---|---|---|---|---|
| Global, location | Intensity-dependent, location | Print tip-dependent, location | Print tip, location and scale | Scale | ||
| c(.) constant, a(.) = 1 | c(.)= c(A), a(.) = 1 | c(.) = c(A, print tip), a(.) = 1 | c(.) = c(A, print tip), a(.) = a(print tip) | |||
| All genes | Assumes the majority of genes in the two mRNA samples have similar overall expression levels | Yes | Yes | Yes | Yes | Yes |
| Housekeeping genes | Usually highly expressed and do not capture intensity-dependent structure | Yes | No | No | No | No |
| MSP titration series | Doesn’t require any prior biological assumption, however, estimating c(A, print tip) based on a small number of spots may not be very stable | Yes | Yes | No | No | No |
| Rank-invariant set | May not span the whole intensity range | Yes | Yes | No | No | No |
For within-slide normalization, the log ratios are normalized by log2R/G → [log2R/G – c(.)]/a(.), where c(.) and a(.) correspond to location and scale adjustment, respectively. The columns refer to different normalization methods and the rows correspond to different sets of control spots. The Yes or No in each cell refers to the feasibility of performing the normalization in practice. For example, it is possible in practice to perform global normalization based only on housekeeping genes, but it is not advisable to perform intensity-dependent normalization on housekeeping genes only.
Acknowledgments
ACKNOWLEDGEMENTS
We would like to acknowledge Matthew J. Callow from the Lawrence Berkeley National Laboratory for providing the data we used to develop the various normalization approaches and Yasushi Okazaki and Yoshihide Hayashizaki of the RIKEN Genomics Sciences Center for graciously providing their normalized mouse cDNA clone set for our use. We would like to thank Elva Diaz, Andrew Finn, Jonathan Scolnick and Tito Serafini for discussions and assistance over the course of this project. We are also grateful to Eric Schadt and Wing Hung Wong for discussions as well as for providing the code for their rank-invariant normalization methods. This work was supported in part by the NIH through grants 5R01MH61665-02 (J.N. and T.P.S.) and 8RO1GM59506A (T.P.S.), by funds from the Department of Molecular and Cell Biology and Helen Wills Neuroscience Institute (University of California at Berkeley) and by a PMMB Burroughs-Wellcome postdoctoral fellowship (S.D.).
REFERENCES
- 1.Taniguchi M., Miura,K., Iwao,H. and Yamanaka,S. (2001) Quantitative assessment of DNA microarrays—comparison with northern blot analyses. Genomics, 71, 34–39. [DOI] [PubMed] [Google Scholar]
- 2.Hughes T.R., Marton,M.J., Jones,A.R., Roberts,C.J., Stoughton,R., Armour,C.D., Bennett,H.A., Coffey,E., Dai,H., He,Y.D., Kidd,M.J., King,A.M., Meyer,M.R., Slade,D., Lum,P.Y., Stepaniants,S.B., Shoemaker,D.D., Gachotte,D., Chakraburtty,K., Simon,J., Bard,M. and Friend,S.H. (2000) Functional discovery via a compendium of expression profiles. Cell, 102, 109–126. [DOI] [PubMed] [Google Scholar]
- 3.Spellman P.T., Sherlock,G., Zhang,M.Q., Iyer,V.R., Anders,K., Eisen,M.B., Brown,P.O., Botstein,D. and Futcher,B. (1998) Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell, 9, 3273–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Alizadeh A.A., Eisen,M.B., Davis,R.E., Ma,C., Lossos,I.S., Rosenwald,A., Boldrick,J.C., Sabet,H., Tran,T., Yu,X., Powell,J.I., Yang,L., Marti,G.E., Moore,T., Hudson,J.,Jr, Lu,L., Lewis,D.B., Tibshirani,R., Sherlock,G., Chan,W.C., Greiner,T.C., Weisenburger,D.D., Armitage,J.O., Warnke,R., Staudt,L.M. et al. (2000) Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature, 403, 503–511. [DOI] [PubMed] [Google Scholar]
- 5.Alon U., Barkai,N., Notterman,D.A., Gish,K., Ybarra,S., Mack,D. and Levine,A.J. (1999) Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc. Natl Acad. Sci. USA, 96, 6745–6750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.DeRisi J., Penland,L., Brown,P.O., Bittner,M.L., Meltzer,P.S., Ray,M., Chen,Y., Su,Y.A. and Trent,J.M. (1996) Use of a cDNA microarray to analyse gene expression patterns in human cancer. Nature Genet., 14, 457–460. [DOI] [PubMed] [Google Scholar]
- 7.Golub T.R., Slonim,D.K., Tamayo,P., Huard,C., Gaasenbeek,M., Mesirov,J.P., Coller,H., Loh,M.L., Downing,J.R., Caligiuri,M.A., Bloomfield,C.D. and Lander,E.S. (1999) Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science, 286, 531–537. [DOI] [PubMed] [Google Scholar]
- 8.Perou C.M., Jeffrey,S.S., van de Rijn,M., Rees,C.A., Eisen,M.B., Ross,D.T., Pergamenschikov,A., Williams,C.F., Zhu,S.X., Lee,J.C., Lashkari,D., Shalon,D., Brown,P.O. and Botstein,D. (1999) Distinctive gene expression patterns in human mammary epithelial cells and breast cancers. Proc. Natl Acad. Sci. USA, 96, 9212–9217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ross D.T., Scherf,U., Eisen,M.B., Perou,C.M., Rees,C., Spellman,P., Iyer,V., Jeffrey,S.S., Van de Rijn,M., Waltham,M., Pergamenschikov,A., Lee,J.C., Lashkari,D., Shalon,D., Myers,T.G., Weinstein,J.N., Botstein,D. and Brown,P.O. (2000) Systematic variation in gene expression patterns in human cancer cell lines. Nature Genet., 24, 227–235. [DOI] [PubMed] [Google Scholar]
- 10.Dudoit S., Yang,Y.H., Callow,M.J. and Speed,T.P. (2002) Statistical methods for identifying genes with differential expression in replicated cDNA microarray experiments. Stat. Sin., in press. [Google Scholar]
- 11.The Chipping forecast. (1999) Nature Genet., 21 (suppl.). [Google Scholar]
- 12.Marton M.J., DeRisi,J.L., Bennett,H.A., Iyer,V.R., Meyer,M.R., Roberts,C.J., Stoughton,R., Burchard,J., Slade,D., Dai,H., Bassett,D.E.,Jr, Hartwell,L.H., Brown,P.O. and Friend,S.H. (1998) Drug target validation and identification of secondary drug target effects using DNA microarrays. Nature Med., 4, 1293–1301. [DOI] [PubMed] [Google Scholar]
- 13.Shoemaker D.D., Schadt,E.E., Armour,C.D., He,Y.D., Garrett-Engele,P., McDonagh,P.D., Loerch,P.M., Leonardson,A., Lum,P.Y., Cavet,G., Wu,L.F., Altschuler,S.J., Edwards,S., King,J., Tsang,J.S., Schimmack,G., Schelter,J.M., Koch,J., Ziman,M., Marton,M.J., Li,B., Cundiff,P., Ward,T., Castle,J., Krolewski,M., Meyer,M.R., Mao,M., Burchard,J., Kidd,M.J., Dai,H., Phillips,J.W., Linsley,P.S., Stoughton,R., Scherer,S. and Boguski,M.S. (2001) Experimental annotation of the human genome using microarray technology. Nature, 409, 922–927. [DOI] [PubMed] [Google Scholar]
- 14.Callow M.J., Dudoit,S., Gong,E.L., Speed,T.P. and Rubin,E.M. (2000) Microarray expression profiling identifies genes with altered expression in HDL-deficient mice. Genome Res., 10, 2022–2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Miki R., Kadota,K., Bono,H., Mizuno,Y., Tomaru,Y., Carninci,P., Itoh,M., Shibata,K., Kawai,J., Konno,H., Watanabe,S., Sato,K., Tokusumi,Y., Kikuchi,N., Ishii,Y., Hamaguchi,Y., Nishizuka,I., Goto,H., Nitanda,H., Satomi,S., Yoshiki,A., Kusakabe,M., DeRisi,J.L., Eisen,M.B., Iyer,V.R., Brown,P.O., Muramatsu,M., Shimada,H., Okazaki,Y. and Hayashizaki,Y. (2001) Delineating developmental and metabolic pathways in vivo by expression profiling using the RIKEN set of 18,816 full-length enriched mouse cDNA arrays. Proc. Natl Acad. Sci. USA, 98, 2199–2204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Buckley M.J. (2000) The Spot User’s Guide. CSIRO Mathematical and Information Sciences, North Ryde, NSW 1670, Australia. http://www.cmis.csiro.au/iap/spot.htm
- 17.Ihaka R. and Gentleman,R. (1996) R: a language for data analysis and graphics. J. Comput. Graph. Statist., 5, 299–314. [Google Scholar]
- 18.Westfall P.H. and Young,S.S. (1993) Resampling-based Multiple Testing: Examples and Methods for P-value Adjustment. Wiley, New York.
- 19.Schadt E., Li,C., Ellis,B. and Wo,W.H. (1999) Feature extraction and normalization algorithms for high-density oligonucleotide gene expression array data. Department of Statistics, UCLA. Preprint 303, www.stat.ucla.edu [DOI] [PubMed]
- 20.Tseng G.C., Oh,M.K., Rohlin,L., Liao,J. and Wong,W.H. (2001) Issues in cDNA microarray analysis: quality filtering, channel normalization, models of variations and assessment of gene effects. Nucleic Acids Res., 29, 2549–2557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yang Y.H., Dudoit,S., Luu,P. and Speed,T.P. (2001) Normalization for cDNA microarray. In Bittner,M.L., Chen,Y., Dorsel,A.N. and Dougherty,E.R. (eds), Microarrays: Optical Technologies and Informatics. SPIE, Society for Optical Engineering, San Jose, CA.
- 22.Chen Y., Dougherty,E.R. and Bittner,M.L. (1997) Ratio-based decisions and the quantitative analysis of cDNA microarray images. J. Biomed. Optics, 2, 364–374. [DOI] [PubMed] [Google Scholar]
- 23.Newton M.A., Kendziorski,C.M., Richmond,C.S., Blattner,F.R. and Tsui,K.W. (2001) On differential variability of expression ratios: improving statistical inference about gene expression changes from microarray data. J. Comput. Biol., 8, 37–52. [DOI] [PubMed] [Google Scholar]
- 24.Axon Instruments Inc. (1999) GenePix 4000A User’s Guide. Axon Instruments, Union City, CA.
- 25.Kerr M.K., Martin,M. and Churchill,G.A. (2000) Analysis of variance for gene expression microarray data. J. Comput. Biol., 7, 819–837. [DOI] [PubMed] [Google Scholar]
- 26.Finkelstein D.B., Gollub,J., Ewing,R., Sterky,F., Somerville,S. and Cherry,J.M. (2000) Iterative linear regression by sector: renormalization of cDNA microarray data and cluster analysis weighted by cross homology. In CAMDA. http://afgc.stanford.edu/afgc_html/site2Stat.htm
- 27.Sapir M. and Churchill,G.A. (2000) Estimating the posterior probability of differential gene expression from microarray data, Poster. The Jackson Laboratory. www.jax.org/research/churchill/pubs
- 28.Kepler T.B., Crosby,L. and Morgan,K.T. (2000) Normalization and analysis of DNA microarray data by self-consistency and local regression. Santa Fe Institute. 00-99-055, www.santafe.edu/sfi/publications/00wplist.html [DOI] [PMC free article] [PubMed]