Prediction of plant complex traits via integration of multi-omics data

Wang, Peipei; Lehti-Shiu, Melissa D.; Lotreck, Serena; Segura Abá, Kenia; Krysan, Patrick J.; Shiu, Shin-Han

doi:10.1038/s41467-024-50701-6

Download PDF

Article
Open access
Published: 10 August 2024

Prediction of plant complex traits via integration of multi-omics data

Nature Communications volume 15, Article number: 6856 (2024) Cite this article

3877 Accesses
Metrics details

Subjects

Abstract

The formation of complex traits is the consequence of genotype and activities at multiple molecular levels. However, connecting genotypes and these activities to complex traits remains challenging. Here, we investigate whether integrating genomic, transcriptomic, and methylomic data can improve prediction for six Arabidopsis traits. We find that transcriptome- and methylome-based models have performances comparable to those of genome-based models. However, models built for flowering time using different omics data identify different benchmark genes. Nine additional genes identified as important for flowering time from our models are experimentally validated as regulating flowering. Gene contributions to flowering time prediction are accession-dependent and distinct genes contribute to trait prediction in different genotypes. Models integrating multi-omics data perform best and reveal known and additional gene interactions, extending knowledge about existing regulatory networks underlying flowering time determination. These results demonstrate the feasibility of revealing molecular mechanisms underlying complex traits through multi-omics data integration.

Crop-GPA: an integrated platform of crop gene-phenotype associations

Article Open access 12 February 2024

Transcriptome-wide association analyses reveal the impact of regulatory variants on rice panicle architecture and causal gene regulatory networks

Article Open access 18 November 2023

Dual-trait genomic analysis in highly stratified Arabidopsis thaliana populations using genome-wide association summary statistics

Article 31 May 2024

Introduction

Translating genotypes to phenotype is challenging because the genetic mechanisms underlying trait variation are complex. Although genetic variation information is commonly used to predict phenotypes (i.e., genomic prediction)^1,2, researchers have had success in using other types of data. For example, transcriptomic data have been used to predict flowering time and yield³ and pathogen resistance in plants⁴; methylomic data have been used to predict flowering time and plant height in a panel of epigenetic recombinant inbred lines of Arabidopsis thaliana^5,6; and metabolomic data have been used to predict biomass- and bioenergy-related traits in maize⁷ and yield in rice⁸. Although multi-omics datasets that align with trait variation information are scarce in non-medical, multicellular model systems, the Arabidopsis 1001 Genome Project has generated phenotypic, genomic (G, i.e., biallelic single nucleotide polymorphisms [SNPs]), transcriptomic (T, RNA sequencing), and methylomic (M, gene-body methylation [gbM], or single site-based methylation [ssM]) data for hundreds of accessions of the model plant A. thaliana^9,10. The availability of these datasets provides an opportunity to predict complex traits using machine learning approaches by integrating different data types. Through interpreting these machine learning models, gene features important for prediction of complex traits can be identified to gain a deeper insight into the mechanistic basis of complex traits beyond the few significant quantitative trait loci (QTLs) that can be revealed through genome-wide association studies (GWAS).

In this work, we assess how the G, T, and M data can be used in predicting six Arabidopsis traits (Fig. 1a, a flow chart illustrating the steps in this study is shown in Fig. 1). To obtain a rough estimate of how well the trait variation can be reflected by omics data variation, we first compare the omics similarity matrices among Arabidopsis accessions with the trait similarity matrices (Fig. 1b). Then we generate models for predicting six traits using G, T, and M data independently (Fig. 1c). To better interpret the predictive models, we compare the genes important for flowering time prediction with benchmark genes that are known to regulate flowering. Finally, feature interactions are investigated by interpreting the integrated models built using all the G, T, and M features for the benchmark genes (Fig. 1e).

**Fig. 1: Flow chart of our methodology.**

Results

Prediction of complex traits using individual omics data

The six traits, namely flowering time (days until the first flower was open), rosette leaf number (RLN), cauline leaf number (CLN), diameter of the rosette (DoR), rosette branch number (RBN), and stem length (SL), were collected for 383 Arabidopsis accessions from published studies^9,10,11 (Fig. 1a, Supplementary Data 1). Samples for G, T, and M were taken from mixed rosette leaves harvested just before bolting at 22 °C, flowering time was measured at 10 °C, and the other five traits were measured at 16 °C^9,10,11. Before investigating the utility of different omics data for plant complex trait prediction, we first examined the omics data structure among accessions (Fig. 1b), with the assumption that accessions with more similar trait values are expected to have more similar genetic information (i.e., G, T, or gbM). However, G, T, or gbM data alone explained only a small amount of variation, as there was no obvious relationship between the trait and omics similarity matrices: the Pearson’s r between phenotypic trait similarity among accessions (pCor; e.g., pCor_{flowering time} see Supplementary Fig. 1a) and the corresponding similarity of G (kinship, Supplementary Fig. 1b), T (eCor, Supplementary Fig. 1c), and gbM (mCor, Supplementary Fig. 1d) only ranged from −0.02 to 0.17 (Fig. 2a). This weak correlation is consistent with the findings in our previous study of yield, height, and flowering time in maize³, and is expected because only a subset of G/T/gbM variants (e.g., a few SNPs) are expected to contribute to the variation in a complex trait, and the linear correlation between the whole set of variants (e.g., all SNPs) and complex trait values is low. In contrast, kinship and mCor were correlated with each other at a higher level (r = 0.43, Fig. 2a), indicating that gbM is more heritable than phenotypic traits, or that the M data were confounded by G, which will be discussed later on.

**Fig. 2: Relationships between omics data and traits, and trait prediction model performance.**

While the overall correlations are low, the likelihood that predictive information is encoded within the overall G/T/gbM data led us to build machine learning models to take advantage of all features from single omics data for trait prediction. We established single omics data-based trait prediction models using the algorithms ridge regression Best Linear Unbiased Prediction (rrBLUP)¹² and Random Forest (RF)¹³, and the model performance was assessed using a hold-out test dataset and measured as the Pearson Correlation Coefficient (PCC) between true and predicted trait values (see Methods and Fig. 1c). In a previous study we found that, despite their simplicity, rrBLUP and RF outperformed other commonly used algorithms for most species and traits tested¹⁴; furthermore, RF has the advantage of allowing interpretation of the resulting models, in particular allowing identification of non-linear interactions between predictors. In addition to the whole set of features for each omics data, the similarity matrices of omics data (i.e., kinship, eCor, and mCor, which are derived from G, T, and gbM, respectively) were also used to build models. As expected, the higher the correlation between the omics data and trait values (Fig. 2a), the higher the model performance was for most traits and omics data types (Fig. 2b, Supplementary Fig. 2a–d). For each trait, model performance was similar regardless of algorithm or whether omics data values or value similarities among accessions were used as predictive features (Fig. 2b, Supplementary Fig. 2a, e). Most importantly, G-, T-, and gbM-based models had comparable performances (Fig. 2b, Supplementary Fig. 2a). For example, G- and T-based rrBLUP models had the highest performance for flowering time and CLN, respectively, whereas gbM-based RF models had the highest performance for flowering time. This is consistent with the findings of our previous maize study using both G and T data for trait prediction³.

Since CG, CHG, and CHH methylation have different regulatory mechanisms and functions in plants¹⁵, we also established models using the different gbM types as separate features. Models using individual gbM data types tended to have similar or poorer performances than models using combined gbM data, and models using CHH methylation tended to have the worst performance (Fig. 2b, Supplementary Fig. 2a). Because of the complexity of M data (e.g., heterogeneity in numbers of methylated cytosine sites within genic regions), we also explored six additional derived M features (single site-based M, hereafter referred to as ssM, see Methods) for predicting flowering time as an example. rrBLUP models using ssM features had higher prediction accuracies than those using gbM (Supplementary Fig. 3a, b), but the prediction accuracies for RF models were not higher for unknown reasons (Supplementary Fig. 3c, d). The improved prediction of ssM-based rrBLUP models may be because the ssM features captured the distribution of methylation across each gene, which provided more detailed information about methylation patterns than the gbM data. Taken together, these results indicate that, similar to G and T data^3,16, M data are also useful for predicting plant traits, and that M data need to be represented in different ways to maximize their predictive power.

Distinct contributions of omics data to complex trait predictions

To identify the informative variants embedded in the G/T/gbM data, we investigated the importance of features for trait prediction by interpreting the prediction models. Three measures were used to evaluate feature importance: (1) coefficients of features in the rrBLUP models (Supplementary Fig. 4a–c); (2) gini importances in the RF models (Fig. 3a–c); and (3) the average absolute SHapley Additive exPlanations (SHAP) values¹⁷ obtained from RF models (Supplementary Fig. 4d–f). Here, we focus on features important for predicting flowering time (for feature importances for the other five traits, see Supplementary Data 2–7) because there is abundant knowledge about the genetic control of this trait, which is crucial for interpreting the important features. To allow for a comparison of importances with T and gbM features, which are gene-based, G variants were mapped to genic regions (see Methods). Genes corresponding to or harboring important G/T/gbM features (defined as those with >95^th percentile importance values) were considered important for flowering time prediction and are hereafter referred to as important genes. We found weak or no correlation between importance scores from models built using different types of omics data, regardless of the feature importance measure examined (Spearman’s ρ: −0.07–0.11), and there was little overlap of important genes between models (Fig. 3, Supplementary Fig. 4a–f).

**Fig. 3: Correlation of feature importance between different types of omics data.**

These results suggest that the similar trait prediction accuracy of models built with different omics data is not due to shared features, consistent with the findings of the maize study³. However, the correlation between the importance of G and gbM variants (Fig. 3b, Supplementary Fig. 4b, e) was higher than that for other comparisons, consistent with the relatively higher correlation between G and gbM similarities across accessions (i.e., kinship and mCor, Pearson’s r = 0.43, Fig. 2a) and suggesting potential confounding effects of G on gbM data. To disentangle gbM from G data, we built trait prediction models with the mCor residuals to exclude the kinship effects (Methods). Consistent with a confounding effect of G on gbM, these new models had significantly lower performance compared with models based on the mCor matrix for all traits (differences in PCC scores, which were used as measures of prediction accuracy: 0.01–0.18, p from two-sided Wilcoxon rank sum test <0.05) (Supplementary Fig. 4g). However, mCor-based models with confounding effects of kinship removed still performed better at predicting flowering time and RLN than those using the first five principal components of G data to approximate population structure (Supplementary Fig. 4g, the performance of the population structure-based model is used as the baseline for trait prediction). Thus, the components of gbM independent from G are also important for trait prediction.

Benchmark flowering time genes identified as important features in flowering time prediction models

In the previous section we showed that models built using different omics data identified different important genes (Fig. 3, Supplementary Fig. 4a–f). We next asked how many genes with known functions in flowering time were identified as important genes. We downloaded 426 benchmark flowering time genes from FLOR-ID (http://www.phytosystems.ulg.ac.be/florid/)¹⁸ and TAIR (https://www.arabidopsis.org/) (Supplementary Data 8), and found that 169 were identified as important according to at least one of the three importance measures for at least one of the three individual omics datasets (Fig. 4, for full gene list, see Supplementary Data 9). Only two genes, FLOWERING LOCUS C (FLC) and its paralog MADS AFFECTING FLOWERING 2 (MAF2), were identified as important by all three independent omics datasets (orange font, Fig. 4). This is consistent with the roles of FLC^10,19,20 and MAF2^21,22 in flowering time regulation being established through studies of genetic variation, transcript levels, and methylation levels. Another 27 genes (blue font, Fig. 4) were identified by two independent omics datasets. For instance, FLOWERING CONTROL LOCUS A (FCA), which increases H3K4 dimethylation in the central region of FLC and regulates its expression²³, was considered important in the G and gbM models. The remaining 140 genes were dataset specific (black font in Fig. 4, and Supplementary Data 9), such as SUPPRESSOR OF OVEREXPRESSION OF CO 1 (SOC1), which was only identified as important in T models. This is consistent with our observations that there is little overlap between important genes identified by G, T, and gbM models (Fig. 3, Supplementary Fig. 4a–f), and that gbM data, although it is confounded with G information (Supplementary Fig. 4g), can make unique contributions.

**Fig. 4: Example benchmark flowering time genes identified using different importance measures and datasets.**

We next asked whether significantly more benchmark flowering time genes than random chance were identified by our models. When the 95^th percentile was used as the threshold, only G and T models with RF gini importance scores identified significantly higher proportions of benchmark genes (8.78% and 8.62%, respectively) than expected by random chance (p = 1.22e-03 and 1.76e-03, respectively, Fisher’s exact test, Supplementary Data 10). To understand why no more benchmark genes were identified than expected by random chance for most models and importance measures, we explored the following potential factors (for the rationale and analysis process, see Methods): cut-off threshold (95^th or 99^th percentile), the number of accessions used for training models, and difference in gene contributions to flowering in short days (SDs) and/or long days (LDs). The former two factors had little impact on the identification of benchmark genes (Supplementary Data 10–12), except for SHAP values when the 99^th percentile was used, where significantly more benchmark genes than expected by random chance were identified for the G and T models (Supplementary Data 11). In addition, genes that when mutated or overexpressed had flowering time phenotypes in two conditions (SDs and LDs) were more likely to be identified using our approaches than those that only had a phenotype when mutated or overexpressed in a single condition (SDs or LDs) (Supplementary Data 10, 11).

One thing worth noting is that gbM-based models identified no more benchmark genes as important than expected by random chance, regardless of the threshold used (Supplementary Data 10–12). This may be because gbM does not adequately represent the methylation profiles of a given gene. To assess this, we also interpreted ssM-based models in which the methylation profile across a gene region was represented (see Methods). An additional 144 benchmark flowering time genes were recovered as important by at least one ssM feature type/feature importance measure combination (Supplementary Data 9), and more benchmark genes were identified as important for a single ssM model (a maximum of 44 genes, Supplementary Data 13) than a single gbM model (a maximum of 24 genes, Supplementary Data 10). One example gene is CLEAVAGE STIMULATION FACTOR 77 (CSTF77), which is involved in the 3’ processing of antisense FLC mRNA²⁴. Accessions with CG-type methylation at two different sites in CSTF77 had significantly longer flowering times than those without (Supplementary Fig. 5a, b), but there were no significant differences in flowering time between accessions with different SNP alleles (Supplementary Fig. 5c, d). In addition, there was no correlation between the expression levels or gbM levels of CSTF77 and flowering time (Supplementary Fig. 5e–h). These results explain why CSTF77 was uniquely identified by ssM-based models (Supplementary Data 9).

Another potential reason for the low degree of enrichment of identified benchmark genes for most models is the fact that the plants scored for flowering time phenotypes were grown at 10 °C and those used for the G, T, and M data were grown at 22 °C. We also built models using the same G/T/gbM data to predict flowering time phenotypes recorded at 16 °C¹⁰, and found that the temperature at which flowering time was scored affected gene importance for flowering time prediction (Supplementary Data 14,15). For example, the expression of FRIGIDA (FRI), which, when functional, confers a vernalization requirement²⁵, had a SHAP value of zero for flowering time prediction at 10 °C but a SHAP value of 0.075 (ranked 14^th) at 16 °C (Supplementary Fig. 6a). This is consistent with the larger differences in flowering time between accessions with functional and non-functional FRI copies at 16 °C than at 10 °C (a temperature at which the vernalization requirement is met for accessions with functional FRI); the larger SHAP values for FRI in the 16 °C model indicate that it makes a higher contribution to flowering time prediction when the plants are not vernalized (Supplementary Fig. 6b). Furthermore, the higher importance rank of FRI features at 16 °C compared with 10 °C was also observed for all G- and T-models regardless of the importance measure examined (Supplementary Fig. 6c, d, and Supplementary Data 14, 15).

Since a number of benchmark flowering time genes were identified when RLN and CLN were used as proxies for flowering time in some previous studies, we also asked how many benchmark flowering time genes could be identified by the RLN and CLN models. When only G-, T-, and gbM-based models were examined, 42 genes were identified as important by all flowering time, RLN, and CLN models (Supplementary Data 16); these are generally hub genes in the flowering time regulation network, such as FT, FLC, SOC1, FRI, BROTHER OF FT AND TFL1 (BFT), and SHORT VEGETATIVE PHASE (SVP)²⁶. Consistent with the importance of FRI for predicting flowering at 16 °C, FRI was important for predicting RLN and CLN in both G- and T-models, probably because the temperature (16 °C) was the same as that at which RLN and CLN were measured. An additional 20 benchmark genes were identified as important by both RLN and CLN models, and 37 and 49 were specifically identified by RLN and CLN models, respectively. For example, TIMING OF CAB EXPRESSION 1 (TOC1) was previously shown to control photoperiodic flowering response when RLN was used as a proxy for flowering time²⁷. Consistent with this, TOC1 only had importance ranks above 95^th percentile in G models for RLN. In our prediction models, TERMINAL FLOWER 1 (TFL1) was only important for CLN prediction, which is consistent with the previous finding that tfl1 mutants showed significantly decreased CLN, but not RLN or days to bolting (another proxy for flowering time), compared with wild type (WT)²⁸. Taken together, these results indicate that different omics datasets, ways to represent data, importance measures, environmental factors, and ways to measure traits must be considered to better capture the genetic basis of Arabidopsis flowering time and likely other complex traits.

Identification of additional genes involved in regulating flowering time

To determine whether all the features relevant to benchmark flowering time genes are sufficient to predict flowering time, we built RF models using G, T and gbM features for 426 benchmark genes separately or combined (hereafter referred to as benchmark gene-based models). Compared with the corresponding full models built using the features for all genes, the benchmark gene-based models had significantly lower performance for gbM-based and the combined models (Fig. 5a), suggesting that genes in addition to the 426 benchmark genes are involved in regulating flowering time. To test this, we selected the 426 most important genes that were not benchmark genes (hereafter referred to as “top non-benchmark” genes) from the full model, which was built using G/T/gbM features combined for all genes (Supplementary Data 17). We found that the top non-benchmark gene-based gbM model (built using the gbM features of these top non-benchmark genes) performed significantly better than the benchmark gene-based gbM model, but not the corresponding G-, T-, and combined models (Fig. 5a). This may be attributed to the fact that most benchmark flowering time genes were identified using genetic approaches (e.g., via forward genetic screens or GWAS) and/or transcriptomic data (e.g., via gene differential expression analysis), rather than methylomic data.

**Fig. 5: Identification of additional genes involved in flowering time regulation.**

To validate the functions of important genes in flowering time, we took advantage of an existing dataset in our lab to compare flowering time in mutants of 21 non-benchmark genes that were identified as important and the WT (Methods, Supplementary Data 18, 19). Six of these 21 genes affected flowering time when mutated (Fig. 5b–f). For example, a loss-of-function mutant of AT4G11070 (WRKY41), which controls seed dormancy²⁹, flowered significantly earlier than WT (Fig. 5c). Consistent with this, WRKY41’s homolog Dlf1 regulates flowering in rice³⁰. Another three genes had loss-of-function effects on flowering when mutated along with their paralogs (Fig. 5g, h). The remaining 12 genes did not have a significant effect on flowering time when mutated, alone or with their paralogs (Supplementary Data 18). One potential explanation for why no flowering time phenotype was observed for these 12 important genes is that our validation experiments were conducted in the Col-0 genetic background, but the important genes were identified in models built across multiple accessions.

To check whether our models perform well in identifying genes that function in flowering time, we also measured the flowering time of the loss-of-function mutants of 37 “non-important” (importance rank ≤95^th percentile) genes and their paralogs. We found that 43.2% (16 genes) had significantly altered flowering time when mutated (Supplementary Data 18, 19). This percentage is only slightly lower than that of experimentally validated important genes (42.9%, 9 out of 21 genes). One potential explanation for the similar percentages of predicted important and “non-important” genes with experimentally validated roles in flowering time is that, as discussed above, the importance of these genes may be dependent on the accessions and/or environmental conditions. In addition, there are far more features (e.g., >20,000 T features) than instances (only 383 accessions) in our models. Therefore, we do not have enough power to detect variants with significant but lower degrees of contribution to flowering time. Our false negative rate when using importance rank as a criterion is expected to be high.

Accession-dependent contributions of genes to flowering time prediction

Thus far, we have evaluated the contribution of G, T, and gbM features associated with genes to the prediction of flowering time across accessions by dissecting the models through global interpretation³¹. However, some genes may be important contributors to flowering time only in specific accessions. To assess this, we determined the contributions of important features to flowering time in each accession (local interpretation) by examining the SHAP value for each feature in each accession (individual SHAP values, as opposed to the averaged value discussed earlier, see Methods). Here, a positive SHAP value for a feature in an accession means that the value of the feature in that accession contributed to a higher predicted trait value, i.e., longer flowering time. A negative SHAP indicates the opposite: the feature value contributed to reduced flowering time in an accession. The absolute SHAP value describes the degree of feature contribution to trait prediction. Here we first present the SHAP values of the top 20 important genes from the T model in detail as an example because more benchmark genes were among the top 20 genes in this model (Supplementary Fig. 7a) than in the G (Supplementary Fig. 7b) and gbM models (Supplementary Fig. 7c). Organizing the accessions into clusters based on SHAP values of the top 20 T features allowed us to examine the way that different features contribute to flowering time prediction. The accessions we examined formed eight clusters (Fig. 6a), and flowering time varied greatly across these clusters (Fig. 6b).

**Fig. 6: Accession-dependent effects of transcriptome features on flowering time.**

In cluster 1 and 2 accessions (Fig. 6a, b, d, e), the SHAP values for SOC1, FT, and FLC expression were all positive, indicating they contribute to longer flowering time. Their positive contribution is mainly due to lower SOC1 and FT expression and higher FLC expression compared with other accessions (Fig. 6c). In cluster 8 accessions (Fig. 6a, b), all three genes have negative SHAPs, and the shorter flowering time (Fig. 6e) is due to higher SOC1 and FT expression but lower FLC expression (Fig. 6c). This is consistent with earlier findings that SOC1 and FT promote flowering³², FLC represses flowering³³, and the expression levels of SOC1 and FT are negatively correlated with FLC expression³⁴. This coupling between SOC1, FT, and FLC in terms of expression (Fig. 6c, Supplementary Fig. 8a, b, f, g), SHAP values (Fig. 6d, Supplementary Fig. 8c), and flowering time contribution (Fig. 6e, Supplementary Fig. 8e) is the predominant flowering time regulatory mechanism for most accessions. However, the action of these components can be decoupled. For example, in cluster 4, 5, and 6 accessions (dots in the second and fourth quadrants, Fig. 6d), the SHAP values of SOC1 and FT have opposite signs, which is associated with moderate flowering time values (Fig. 6b, e). Another example is cluster 7 (orange dots in the third quadrant, Fig. 6d) where, despite the positive contribution of FLC (Fig. 6a, Supplementary Fig. 8c), both SOC1 and FT contribute negatively to flowering time (Fig. 6d). This coupling and uncoupling between SOC1, FT, and FLC expression across accessions indicates that regulation of flowering time may be more complex than what has been reported. Accession-dependent contributions of other important T features are also observed, although to a much lower extent. An example is SQUAMOSA PROMOTER BINDING PROTEIN-LIKE 15 (SPL15); clusters 2 and 4–8 can be divided into sub-clusters depending on whether SPL15 expression contributes positively to flowering time in an accession (Fig. 6a).

We also clustered accessions using SHAP values of the top 20 important features from G and gbM models, and obtained eight and nine clusters, respectively (Supplementary Fig. 9a, c), which resembled the distribution of T model-based clusters in that the clusters could be characterized by a few top features. For example, the second (AT4G38550) and the third (AT1G35610) most important genes from the gbM model can be coupled or uncoupled with FLC in a similar fashion as SOC1 and FT (Supplementary Fig. 9c). The different omics data types yielded clusters with different accessions (Supplementary Fig. 10). These findings further demonstrate that different omics data reveal different contributors to flowering time variation among accessions, and that the different effects of genes on flowering time among accessions can be disentangled through model interpretation. In addition, knowledge about flowering regulation in some accessions may not be generalizable to others, as demonstrated by the identification of different benchmark genes when different sets of accessions were used (Supplementary Data 10, 12). This may be explained by the differences in genetic backgrounds among accessions²⁵ and the high complexity of genetic interaction networks regulating flowering³⁵. The accession-dependent effects of genes on flowering may also partially explain the low degree of enrichment of benchmark genes among important genes in our original G, T, and gbM models because these benchmark genes were predominantly discovered in the Col-0 accession.

Genetic interactions revealed through integration of multi-omics data

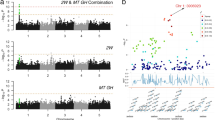
In the above sections we showed that different types of omics data revealed overlapping but mostly distinct genes impacting flowering time. Next, we asked whether combining different types of omics data improves the prediction accuracy. We found that combining G and T or all three datasets improved model performance for RF models, but not for rrBLUP models (Fig. 7a). Because the RF algorithm considers non-linear feature combinations while rrBLUP does not, the better RF model performance suggests that the inclusion of interactions between features from different omics data may have improved model performance. To evaluate this possibility, we established an additional RF model, which only included G + T + gbM features relevant to the 426 benchmark flowering time genes (see Methods) to facilitate model interpretation. We used the SHAP approach³⁶ to identify feature interactions (see Methods), where the contribution of feature X to trait prediction is influenced by values of feature Y. The SHAP feature interaction can help us identify potential genetic interactions between genes or variants, such as epistasis³⁷. We identified 7,186 feature interactions, including all six possible combinations between omics data types: G-G, T-T, gbM-gbM, G-T, G-gbM, and T-gbM (Supplementary Data 20). T-gbM, G-T, and T-T interactions were the most prevalent (Fig. 7b). The T-features of three most important genes in the T model—SOC1, FT, and FLC (Fig. 6a)—had the highest numbers of feature interactions (707, 638, and 279, respectively), consistent with their reported functions as floral integrators³², which receive floral promotion or inhibitory signaling inputs from distinct pathways (Fig. 7c, Supplementary Data 20).

**Fig. 7: Prediction models integrating all omics data types and putative interactions between flowering time genes.**

Among the top 20 interactions with the highest interaction values, five were T-T interactions of SOC1 with FT (ranked 1^st), MIR172B (2^nd), SPL5 (13^th), FLC (19^th), and PHYTOCHROME INTERACTING FACTOR 3 (PIF3) (20^th) (Fig. 7c, d, Supplementary Fig. 11a–e). SOC1 was previously shown to regulate MIR172B³⁸ and SPL5³⁹ by directly binding to their promoters. However, no direct biological interaction between SOC1 and PIF3 has been reported. Also among the top 20 interactions, two were T-gbM and T-G interactions of SOC1 with ZEITLUPE (ZTL, ranked 5^th, Fig. 7e) and Nuclear Pore Anchor (NUA, ranked 6^th, Fig. 7f). ZTL and its two homologs, LOV KELCH PROTEIN 2 (gbM-T interaction with SOC1 ranked 121^st, Supplementary Fig. 11f) and FLAVIN-BINDING, KELCH REPEAT, F-BOX 1 (gbM-T interaction with SOC1 ranked 3333^rd, Supplementary Fig. 11g), function as E3 ubiquitin ligases and regulate flowering time regulators, such as CONSTANS and FT ⁴⁰. No direct biological interaction has been reported between SOC1 and ZTL or its two homologs, whereas the interaction between SOC1 and NUA was reported before: expression of SOC1 was higher in nua-1/4 mutants compared with WT⁴¹. In addition to these T-T, T-gbM, and T-G interactions, we also observed G-G, G-gbM, and gbM-gbM interactions that have not been reported before: a G-G interaction between AT1G11520 and HASTY 1 ranked 8^th (Supplementary Fig. 11h), gbM-gbM interaction between VIN3-LIKE 3 and INDUCER OF CBF EXPRESSION 1 ranked 25^th (Supplementary Fig. 11i), and G-gbM interaction between AT1G11520 and FY ranked 45^th (Supplementary Fig. 11j). These interactions might indicate potential biological interactions between genes.

Furthermore, by examining the feature interactions in detail, we found some interesting patterns. For example, the T-gbM interaction between SOC1 and ZTL illustrates how SOC1 and ZTL interact across accessions (Fig. 7e): in accessions with higher SOC1 expression, contributions of ZTL CG-type gbM were near-zero regardless of the methylation levels of ZTL, whereas in accessions with lower SOC1 expression, the contributions were larger either positively or negatively. A similar pattern was also observed for other interactions, such as a T-T interaction between SOC1 and MIR172B (Supplementary Fig. 11b). Taken together, these findings show that potential interactions at different molecular levels can be identified on a large scale by interpreting computational models integrating multiple omics data.

Discussion

We investigated the utility of G, T, and M data in predicting complex traits in Arabidopsis, and found that models built using these data types separately had comparable performances. The flowering time prediction models built using different omics data identified different benchmark flowering time genes and other genes not previously reported to be involved in flowering. Even models built using different forms of a single type of omics data—M data—identified different sets of flowering genes. These results highlight the necessity of exploring different types of omics data when predicting complex traits. Even though there was only one time point for transcriptome data (rosette leaves right before bolting)⁹, key regulators of flowering time, such as FLC, FT, SOC1, and SPL15, were still identified in T-based rrBLUP and RF models. Considering that rrBLUP is an algorithm based on a linear model, this finding indicates that simple, linear combinations of the steady-state expression levels of these genes, which explain a significant portion of the flowering time variation among accessions, can be identified.

We identified important genes including the most well-known flowering time genes; however, the false positive and false negative rates based on the benchmarks were high. Model performance and candidate gene identification can be further improved by incorporating substantially more accessions, using additional approaches to select, combine, and represent features, and incorporating data from more than one environment. In addition, the Arabidopsis T and M data used in this study were obtained from mixed rosette leaves harvested just before bolting, which poses two potential problems for complex trait prediction: (1) gene expression and methylation can be cell-type specific, thus noise in T and M data is inevitable due to cell heterogeneity; (2) the complex traits to be predicted may be specific to certain tissues, organs, or development stages; thus, T and M variation from leaves may not reflect trait variation in other contexts. The development of single-cell and spatial omics techniques, which allow the cellular landscape of epigenomes within a tissue to be measured, is expected to improve the prediction accuracy of complex traits. In addition, omics data in addition to G, T, and M data can be used to predict complex traits; these data include chromatin architecture, chromatin accessibility, and histone modification, changes of which have been shown to regulate flowering in Arabidopsis^39,42,43,44.

The observation that the effects of genes or variants on flowering differ among accessions is known in specific cases. For example, DNA demethylation has different effects on flowering in C24 and Landsberg erecta⁴⁵; some accessions carry non-functional alleles of the FRI gene, thus have no requirement for vernalization before flowering²⁵. Here, we show that accession-specific effects of different flowering time genes can be revealed by interpreting machine learning models. The outcome also revealed accession-dependent effects that were not documented previously. Interpretation of a non-linear model (e.g., RF model) allowed the identification of known interactions and additional interactions that have not been reported previously among G, T, and gbM features of benchmark genes. These additional interactions represent hypotheses that require further experimental verification and are expected to provide insights into how these additional components and interactions contribute to the genetic basis of flowering time and potentially other complex traits.

Methods

Data preprocessing

Six traits for each Arabidopsis accession (Supplementary Data 1) were obtained from two publications: (1) flowering time at 10 °C or 16 °C, which was scored as days until the first flower was open, was from¹⁰; (2) cauline leaf number (CLN), (3) rosette leaf number (RLN), (4) rosette branch number (RBN), (5) diameter of rosette (end point after flowering, DoR), and (6) stem length (length of main flowering stem, SL) were from¹¹. For each trait, the pairwise Euclidean distances of trait values between accessions were calculated using the R package “rdist” (version 0.0.5). The Euclidean distances were first normalized between 0 and 1, and then the correlation or similarity of phenotypic trait values (pCor) among accessions was calculated as 1 - normalized Euclidean distance.

The genomic matrix (G) was downloaded from the 1001 Genomes database¹⁰ (http://1001genomes.org/data/GMI-MPI/releases/v3.1/SNP_matrix_imputed_hdf5/), which contains biallelic SNPs. SNPs with minor allele frequency <0.05 were removed. For each SNP, the major allele was encoded as 1, and the minor allele was encoded as −1. The kinship matrix was generated from G using the KinshipPlugin with the centered Identity By State method⁴⁶ implemented in TASSEL version 5.0⁴⁷. The kinship typically refers to the degree of genetic relatedness between accessions, and was used here as the proxy for the similarity of G among accessions. The first five principal components of G data (used as a proxy for population structure) were generated using the PrincipalComponentsPlugin implemented in TASSEL.

For the transcriptomic (T) data⁹, the normalized read counts were downloaded from NCBI, and were used to calculate the transcripts per million (TPM) using the function “calculateTPM” from the R package “scater” (version 4.4)⁴⁸. The TPM values were then transformed to ln(TPM + 1). The transformed TPM values were used to calculate the expression correlations (eCor) among accessions, and the resultant PCC values were normalized between 0 and 1 to make them comparable with pCor, which ranges from 0 to 1.

For the methylomic (M) data⁹, the gene-body methylation values (gbM, the number of reads with methylated cytosines in a gene body divided by the total number of reads with both cytosines and thymines) were downloaded from http://signal-genet.salk.edu/1001.php. For accessions with multiple replicates, the median values were calculated across replicates. The missing values were imputed using the k-Nearest Neighbors approach (“KNNImputer” function in sklearn.impute)⁴⁹ as follows: missing values in the training set (for the data split into training and test sets, see the Methods section “Predictive modeling”) were first imputed, then the imputation was transformed to the test set. To mitigate potential influences of the selection of k on the imputed missing values, the imputation was conducted five times with different k values (3, 4, 5, 6, and 7), and the means of imputed values were used. The imputed gbM values were used to calculate the gbM correlation (mCor) among accessions, and the resultant PCC values were normalized between 0 and 1.

Additional formats of methylomic data

The frequency of cytosine sites can vary within a genic region, and the methylation level at each cytosine site (i.e., proportion of mapped reads with methylated cytosine) can also vary because of cell heterogeneity; therefore, the gbM obscures information such as heterogeneity in methylation levels over the length of a gene. To overcome these shortcomings, we used six more types of M data (Supplementary Fig. 3) to represent single site-based methylation (ssM) for predicting flowering time: (1) methylation status of single cytosine sites (i.e., 1, indicating methylated, or 0, indicating not methylated, hereafter referred to as presence/absence [P/A] of methylation) across the whole genome; (2) methylation proportion (i.e., proportion [Prop] of reads that were methylated at that site) for single cytosine sites across the whole genome; (3,4) methylation profiles along each gene, i.e., the means of methylation status (3, mean_P/A) or the median methylation proportion (4, med_Prop) across upstream, gene-body, and downstream regions divided into 30 bins; (5,6) clusters of genes with similar methylation profiles when methylation status (5, P/A_clu) or proportion (6, Prop_clu) was considered.

The methylation base calls for each reference site⁹ were downloaded from NCBI (accession ID GSE43857). Missing values in the single cytosine site methylation matrix were treated as follows: (1) if the reference site was a cytosine and there was a SNP for this site in accession X, or if the reference site was not a cytosine and this site was not a SNP for X, the methylation call for this site in X was encoded as 0; (2) if the site’s base in accession X was unknown, or the site in X was a cytosine, but there were no reads mapped to this site, then the values were marked as missing to be imputed in the same way as for the gbM matrices, except that for the P/A of methylation for a single site, the final imputed value was rounded to either 0 or 1. After imputation, sites with the same value (either 0 or 1) in > 95% accessions (similar to 5% minor allele frequency) were removed. To balance the trade-off between the number of methylation sites included in the analysis and the number of missing data points, we first ordered the sites according to the proportion of missing values across accessions. Three thresholds were explored: 90^th, 75^th, and 50^th percentile (the corresponding datasets are referred to hereafter as 90per, 75per, and 50per, respectively), sites above which had missing values in ≤ 2, 8, and 38 accessions, respectively (Supplementary Fig. 12a). We found that the dataset 50per tended to have the highest performance in rrBLUP models while dataset 90per led to the highest performance in RF models (Supplementary Fig. 12b, c). To include more ssM information, matrices using the 50^th percentile as a threshold were used for subsequent analysis.

To bin the methylation levels of single sites for gene-based regions, the gene regions were split into 30 bins as shown in Supplementary Fig. 12d. For each bin, a summary statistic representing the methylation data was calculated: for the methylation P/A, this statistic is the mean number of methylated cytosines in the bin; for methylation proportion, this statistic is the median of the methylation proportion values (a number between 0 and 1) in a bin. To summarize the methylation profiles of genes across accessions, the binned methylation data were formatted into vectors, with one vector of length 30 (the number of bins) for each gene in each accession. These vectors were clustered using K-means clustering (“KMeans” from sklearn.cluster) with 30 clusters. For each gene in each accession, 30 new features (i.e., whether the vector of the gene [methylation profile] belongs to each of the 30 clusters, 1 for the cluster the gene belongs to, 0 for all the other clusters) were produced. Finally, for each feature matrix, columns containing only zeros were removed. These processes were performed on each methylation type separately (CG, CHG, CHH), and matrices of three methylation types were combined together, resulting in 16 final feature matrices (16 “binned” columns in Supplementary Data 9). To simplify our story, these 16 matrics were only used to establish predictive models for flowering time.

Predictive modeling

Twenty percent of the accessions were randomly held out as the test set, which was used to evaluate the performance of final models and was never used in the model training. The remaining 80% of accessions were used to train the models. A five-fold cross-validation (CV) scheme was conducted in the model training. First, the remaining 80% of accessions were randomly split into five folds. Next, accessions in four folds (referred to as the training subset) were used to build the model, and accessions in the fifth fold (validation subset) were used to evaluate the model performance. Finally, this training-validation step was conducted five times to make sure each fold was used as a validation set once. This five-fold CV scheme was repeated 10 times. The PCC was calculated between true trait values and the predicted values of these remaining 80% accessions, and the average PCC among the 10 runs was used to measure the model performance on the CV set.

The R package “rrBLUP” (ridge regression Best Linear Unbiased Prediction, version 4.6.1, installed in R version 3.5.1)¹² and the scikit-learn (version 0.23.1, implemented in Python version 3.6.9) class “RandomForestRegressor” ^13,49 were used to build the predictive models. rrBLUP is a commonly used genomic prediction approach with mixed models, and the key function used in this study was “mixed.solve”, with the equation:

$${{{\rm{y}}}}=\mu+{{{\rm{Xg}}}}+{{{\rm{e}}}}$$

(1)

where y is the vector of trait values, μ is the overall mean of trait values for the training set, X is the feature matrix, g is the feature effect vector (or coefficient vector), and e is the vector of residual effects. The coefficients of features were estimated within each fold of CV and were used to predict trait values for accessions in the validation and test set. After five folds of CV, the prediction accuracies on the test set were averaged to evaluate the model performance, and the coefficients were also averaged.

RandomForestRegressor is a meta estimator that builds various regression decision trees using a number of sub-samples of the dataset. The resulting trees are then aggregated through averaging into a single ensemble model. GridSearch was used for hyperparameter tuning using the “GridSearchCV” function from sklearn.model_selection⁴⁹, where spaces of the parameters -max_depth and -max_features were [3, 5, 10] and [0.1, 0.25, 0.5, 0.75, “sqrt”, “log2”, “None”], respectively. Considering the large numbers of features in the G, T, and M data, we decided to use these small max_depth values to avoid potential over-fitting issues. The parameter -n_estimators was set as 100 and not included in hyperparameter tuning due to high computing resource requirements for large matrices, such as G and ssM-based matrices. The best parameter combination—which was consistent and reproducible—was selected according to the model performances in CV. A final model was built using all the accessions (including accessions in both the training and validation subsets) with the best parameter combination, and was applied on the test set to evaluate the model performance.

To establish the baseline for the genomic prediction, we built predictive models based simply on population structure (defined as first five principal components from genetic markers, as mentioned above, blue dotted line in Fig. 2b) using the training set. Models based on individual omics data outperformed those based on population structure for flowering time, RLN, and CLN, but not for DoR, RBN, and SL. In addition, prediction performances for models based on individual omics data and population structure on the CV and test sets for DoR differed dramatically in both rrBLUP and RF models (Fig. 2b, Supplementary Fig. 2), which is indicative of high heterogeneity in DoR among accessions; the accessions in the training and test sets might have different genetic features affecting DoR. The prediction performances for RBN and SL were relatively low ( < 0.2 and ~0, respectively, Fig. 2b, Supplementary Fig. 2a) no matter which omics data type was used or whether population structure was used to build the models. Therefore, variation in RBN and SL might be mainly explained by the environment and/or genotype-by-environment interactions.

Since there were only 383 accessions that had all three omics data (i.e., G, T and M) and all six types of trait information, we used the data for these 383 accessions for the major analysis in this study. To check whether the data we used were sufficient to produce reasonable results, we also established additional rrBLUP G-based models for flowering time by including data from different numbers of accessions in the training set. There were 618 accessions that had all three omics data and flowering time information; thus, the numbers of accessions in the training set we tested ranged from 31 to 494 (80% of 618 accessions). We found that the prediction performance increased as more accessions were included in the training set, and the performance approached a plateau when n = 221 for both the test (Supplementary Fig. 13a) and validation (Supplementary Fig. 13b) sets. This result suggests that the data we used for our major analysis were sufficient.

To remove the potential confounding effects of kinship on mCor, we estimated linear regression models between mCor and kinship for training accessions (i.e., matrices containing only mCor and kinship values between all accessions [in both the training and test sets] with accessions in the training set) using the “lm” function in R, and then used the residuals of mCor to build a new Random Forest (RF) model.

Feature importance

Three measures were used to evaluate the importance or contributions of features to the prediction of complex traits: (1) RF “gini” importance, which reflects the impurity decrease when a feature is fed to the model⁵⁰; (2) coefficients of features in a rrBLUP regression model; and (3) SHapley Additive exPlanations (SHAP) values of features in an RF model, which reflect the contribution of a feature to the prediction of a complex trait¹⁷. The RF gini importance was obtained from the attribute “feature_importances_” of the fitted RF model, and the rrBLUP coefficient was obtained from the output ($u) of the “mixed.solve” function. The SHAP value was calculated using the function “Explainer” in the SHAP package (version 0.40.0, implemented in Python version 3.6.9). The average absolute SHAP value of a feature for all the instances (local feature importance) was used to measure the global contribution of the feature to model prediction (global feature importance). The former two measures interpret global feature contributions to the model predictions and tend to assign non-zero importance values to all or most features (Fig. 3, Supplementary Fig. 4a–c). In contrast, SHAP values provide local interpretations and tend to assign zero for features that have no contribution to the prediction of flowering time for individual instances (i.e., accessions in this study, Supplementary Fig. 4d–f). A positive SHAP value indicates an instance is predicted to have a higher trait value with a given feature than when that feature is removed from the model, and vice versa. The higher the absolute SHAP value, the more a feature contributes to trait prediction for the instance in question.

Benchmark flowering time genes

We downloaded 378 and 48 benchmark flowering time genes (Supplementary Data 2) from the FLOR-ID database (http://www.phytosystems.ulg.ac.be/florid/)¹⁸ and TAIR (https://www.arabidopsis.org), respectively; these genes are known to be involved in flowering in Arabidopsis. To compare the importance of flowering genes across models built using different omics data, the highest importance (i.e., absolute coefficient in rrBLUP models, RF feature importance, and absolute SHAP values) of all SNPs (or methylation sites) within a gene was used as the gene-based importance. When all three types of gbM data (i.e., CG, CGH, and CHH) were used together, the highest feature importance of the three types was used as the gene-based importance.

To understand why no more benchmark genes at significant levels were identified than random chance for most combinations of omics datasets and importance measures, we explored the following three potential reasons. First, we determined whether the threshold affects the number of identified benchmark genes by increasing the threshold of gene importance scores to the 99^th percentile. The higher the threshold, the fewer benchmark genes were identified, but also the fewer genes were expected (1% for threshold at 99^th percentile). We found that there were significantly more benchmark genes identified than random (1%) only when SHAP values from models built using G and T data were used to identify important genes (Supplementary Data 11), indicating that SHAP values are able to reveal the most important genes (99^th vs. 95^th percentile) for flowering time prediction. However, for all the other combinations of datasets and feature importance measures, no significant differences were observed between results when the 95^th and 99^th percentiles were used as thresholds, indicating that the choice of threshold only had a minor effect on the identification of benchmark genes.

Second, we asked whether the sample size of accessions (306 accessions in the training set, for which data for six traits and all the G, T, and M data were available) was too small. To test this, we repeated the analysis using all 618 accessions (494 accessions were used to train the model, for which all the G, T, and M data and flowering time information were available). Generally, no more benchmark genes were identified than when 306 accessions were used to train the models (Supplementary Data 12), suggesting that decreasing the number of accessions included in the model from 494 to 306 was not a major factor affecting the identification of benchmark genes.

Third, since the functions of benchmark genes in flowering may have been determined under different conditions (e.g., under a different temperature or photoperiod), we investigated whether the use of flowering time data measured under only one condition (at 10 °C)¹⁰ explained the failure to identify more benchmark genes than expected. We reasoned that benchmark genes showing effects on flowering under multiple conditions when mutated or overexpressed would be more likely to contribute to flowering at 10 °C than genes showing effects only under one condition. As expected, we found that genes contributing to flowering under two different conditions (short days [SDs] and long days [LDs], obtained from the FLOR-ID database; unfortunately there were no data for different temperatures) were more likely to be identified than those contributing to flowering only under one condition (Supplementary Data 10,11, Supplementary Fig. 14). In addition, when predicting flowering time measured at 10 °C or 16 °C, genes had different contributions (Supplementary Data 14,15). These findings suggest that the conditions under which the target traits were measured affect which genes are identified as important genes, consistent with the different QTLs identified for flowering time measured at different temperatures¹⁰.

In summary, the threshold used to call important genes and the number of accessions used to train models only had minor, if any, effects on the number of known flowering genes identified. Nevertheless, our feature importance-based approaches outperformed the GWAS approach from a previous study¹⁰, where only five QTLs were identified. Thus, we continued with our original strategy, using the important genes with feature importance scores above the 95^th percentile from models built using 306 accessions, for subsequent analysis.

Plant materials and assessment of flowering time

The potential function in flowering time of 21 genes with importance values above the 95^th percentile (for at least one model based on one of the three omics data combined with one of three importance measures) was validated experimentally. Stock numbers for single-gene T-DNA insertion mutants of these 21 important genes and another 37 non-important genes in the Arabidopsis Col-0 background are listed in Supplementary Data 18. These 58 genes were 29 pairs of paralogs, and the double-mutants of two paralogous genes were produced by crossing the corresponding single-gene mutant lines. The homozygous mutant and WT sibling plants (one to nine plants per genotype, each plant was referred to as a subline) were identified by PCR with gene-specific primers. Five seeds from a single genotype were randomly pipetted into a single cell within a block comprising four 200-cell flats that were filled with Arabidopsis mix (1:1:1 SureMix, vermiculite, and perlite). For each genotype, ≥ 40 seeds (n = 5–20 per subline) were planted. Cells in the outer two rows surrounding the four flats within a block were randomized, and were excluded from the analysis if edge effects were observed. The flats were first stratified for 5–7 days in the dark at 4 °C, and then were transferred to a growth chamber with a 16-h light/8-h dark cycle and a light intensity of 110–130 μmoles m⁻² s⁻¹ at 21 °C. Seedlings were thinned to one per cell after 1 week and plants were watered twice or thrice per week until most plants were mature.

Days to flowering (number of days from placing flats containing seeds in the growth chamber until the appearance of the first open flower) were recorded for at least 17 plants (average = 37.3) per genotype except for AT1G48620/AT3G18035 double mutants, for which flowering was recorded for only three plants (Supplementary Data 19). Within each block, days to flowering observed for plants grown in different flats was first normalized using the function “normalize” of the R package “broman” (version 0.84). Average differences in flowering time between mutants and WT were calculated, and the significance of differences was assessed using the two-sided Wilcoxon rank sum test (Supplementary Data 18).

Feature integration

To investigate interactions among G, T, and gbM features of benchmark flowering time genes, we first built a model using all the features (G + T + gbM) related to the 426 benchmark genes. Then, to simplify the analysis, only one feature each for G (i.e., the SNP having the highest importance rank among other SNPs in a gene), T, and gbM (i.e., CG-, CHG-, or CHH-type gbM, having the highest importance rank among others in a gene) was kept for each gene. This resulted in 1227 features for the 426 genes. A new model was built using these top features, and the interactions among these features were calculated using the “TreeExplainer” and “shap_interaction_values” functions of the SHAP package³⁶. The SHAP interaction between feature i and feature j can be interpreted as the difference in SHAP values of feature i between models with and without the feature j³⁶. The higher the value, the stronger the interaction.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

The biallelic SNP matrix was download from 1001 Genomes Project [https://1001genomes.org/data/GMI-MPI/releases/v3.1/SNP_matrix_imputed_hdf5/1001_SNP_MATRIX.tar.gz] and processed using the script “h5m2csv.py” provided in the same folder. The transcriptomic data (read count files) were downloaded from NCBI with the GEO accession GSE80744. The gene-body methylation data were downloaded from the 1001 Arabidopsis Genomes Project [http://neomorph.salk.edu/downloads/1001/Araport11_GB.tar], and the Arabidopsis accession ID and name information are also provided as “id_name.txt” in the same folder; the single site-based methylation information for individual accessions was downloaded from NCBI with the GEO accession GSE43857. The phenotypes were downloaded from AraPheno, where flowering times measured at 10°C and 16°C were from study:12 [https://arapheno.1001genomes.org/study/12/] and the other five traits were from study:38 [https://arapheno.1001genomes.org/study/38/]. The preprocessed omics data and some intermediate results in this study have been deposited and are freely available at Figshare [https://figshare.com/s/65e1eb61cadae8cbdd96]⁵¹. Source data are provided with this paper.

Code availability

All the scripts used to process the original omics data, build prediction models, and interpret the models in this study are available at Github [https://github.com/ShiuLab/2024_Ath_GP]⁵².

References

VanRaden, P. M. et al. Invited Review: Reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 92, 16–24 (2009).
Article PubMed CAS Google Scholar
Crossa, J. et al. Genomic selection in plant breeding: methods, models, and perspectives. Trends Plant Sci. 22, 961–975 (2017).
Article PubMed CAS Google Scholar
Azodi, C. B., Pardo, J., VanBuren, R., de los Campos, G. & Shiu, S.-H. Transcriptome-based prediction of complex traits in Maize. Plant Cell 32, 139–151 (2020).
Article PubMed CAS Google Scholar
Michel, S. et al. Merging genomics and transcriptomics for predicting fusarium head blight resistance in wheat. Genes 12, 114 (2021).
Article PubMed PubMed Central CAS Google Scholar
Johannes, F. et al. Assessing the impact of transgenerational epigenetic variation on complex traits. PLoS Genet 5, e1000530 (2009).
Article PubMed PubMed Central Google Scholar
Hu, Y., Morota, G., Rosa, G. J. M. & Gianola, D. Prediction of plant height in Arabidopsis thaliana using DNA methylation data. Genetics 201, 779–793 (2015).
Article PubMed PubMed Central CAS Google Scholar
Riedelsheimer, C. et al. Genomic and metabolic prediction of complex heterotic traits in hybrid maize. Nat. Genet 44, 217–220 (2012).
Article PubMed CAS Google Scholar
Hu, X., Xie, W., Wu, C. & Xu, S. A directed learning strategy integrating multiple omic data improves genomic prediction. Plant Biotechnol. J. 17, 2011–2020 (2019).
Article PubMed PubMed Central CAS Google Scholar
Kawakatsu, T. et al. Epigenomic diversity in a global collection of Arabidopsis thaliana accessions. Cell 166, 492–505 (2016).
Article PubMed PubMed Central CAS Google Scholar
Alonso-Blanco, C. et al. 1,135 genomes reveal the global pattern of polymorphism in Arabidopsis thaliana. Cell 166, 481–491 (2016).
Article Google Scholar
Grimm, D. G. et al. easyGWAS: A cloud-based platform for comparing the results of genome-wide association studies. Plant Cell 29, 5–19 (2017).
Article PubMed CAS Google Scholar
Endelman, J. B. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome 4, 250–255 (2011).
Article Google Scholar
Breiman, L. Random forests. Mach. Learn. 45, 5–32 (2001).
Article Google Scholar
Azodi, C. B. et al. Benchmarking parametric and machine learning models for genomic prediction of complex traits. G3 Genes Genomes Genet. 9, 3691–3702 (2019).
Article Google Scholar
Zhang, H., Lang, Z. & Zhu, J.-K. Dynamics and function of DNA methylation in plants. Nat. Rev. Mol. Cell Biol. 19, 489–506 (2018).
Article PubMed CAS Google Scholar
Chien, P.-S., Chen, P.-H., Lee, C.-R. & Chiou, T.-J. TWAS coupled with eQTL analysis reveals the genetic connection between gene expression and flowering time in Arabidopsis. J. Exp. Botany erad262 https://doi.org/10.1093/jxb/erad262 (2023).
Lundberg, S. & Lee, S.-I. A unified approach to interpreting model predictions. arXiv:1705.07874 [cs, stat] (2017).
Bouché, F., Lobet, G., Tocquin, P. & Périlleux, C. FLOR-ID: an interactive database of flowering-time gene networks in Arabidopsis thaliana. Nucleic Acids Res. 44, D1167–D1171 (2016).
Article PubMed Google Scholar
Sheldon, C. C. et al. The FLF MADS Box gene: a repressor of flowering in Arabidopsis regulated by vernalization and methylation. Plant Cell 11, 445–458 (1999).
Article PubMed PubMed Central CAS Google Scholar
Williams, B. P., Bechen, L. L., Pohlmann, D. A. & Gehring, M. Somatic DNA demethylation generates tissue-specific methylation states and impacts flowering time. Plant Cell 34, 1189–1206 (2022).
Article PubMed Google Scholar
Rosloski, S. M., Jali, S. S., Balasubramanian, S., Weigel, D. & Grbic, V. Natural diversity in flowering responses of Arabidopsis thaliana caused by variation in a tandem gene array. Genetics 186, 263–276 (2010).
Article PubMed PubMed Central CAS Google Scholar
Yang, S. et al. Nitrilases NIT1/2/3 positively regulate flowering by inhibiting MAF4 expression in Arabidopsis. Front Plant Sci. 13, 889460 (2022).
Article PubMed PubMed Central Google Scholar
Liu, F. et al. The Arabidopsis RNA-binding protein FCA requires a lysine-specific demethylase 1 homolog to downregulate. Flc. Mol. Cell 28, 398–407 (2007).
Article PubMed Google Scholar
Liu, F., Marquardt, S., Lister, C., Swiezewski, S. & Dean, C. Targeted 3′ processing of antisense transcripts triggers Arabidopsis FLC chromatin silencing. Science 327, 94–97 (2010).
Article ADS PubMed CAS Google Scholar
Zhang, L. & Jiménez‐Gómez, J. M. Functional analysis of FRIGIDA using naturally occurring variation in Arabidopsis thaliana. Plant J. 103, 154–165 (2020).
Article PubMed CAS Google Scholar
Cho, L., Yoon, J. & An, G. The control of flowering time by environmental factors. Plant J. 90, 708–719 (2017).
Article PubMed CAS Google Scholar
Strayer, C. et al. Cloning of the Arabidopsis clock. Gene TOC1 289, 768–771 (2000).
CAS Google Scholar
Cerise, M. et al. Two modes of gene regulation by TFL1 mediate its dual function in flowering time and shoot determinacy of Arabidopsis. Development 150, dev202089 (2023).
Article PubMed PubMed Central CAS Google Scholar
Ding, Z. J. et al. WRKY41 controls Arabidopsis seed dormancy via direct regulation of ABI3 transcript levels not downstream of ABA. Plant J. 79, 810–823 (2014).
Article PubMed CAS Google Scholar
Cai, Y. et al. Dlf1, a WRKY transcription factor, is involved in the control of flowering time and plant height in rice. PLoS One 9, e102529 (2014).
Article ADS PubMed PubMed Central Google Scholar
Azodi, C. B., Tang, J. & Shiu, S.-H. Opening the black box: interpretable machine learning for geneticists. Trends Genet 36, 442–455 (2020).
Article PubMed CAS Google Scholar
Lee, J. H. et al. Integration of floral inductive signals by flowering locus T and suppressor of overexpression of Constans 1. Physiol. Plant 126, 475–483 (2006).
Article CAS Google Scholar
Rouse, D. T., Sheldon, C. C., Bagnall, D. J., Peacock, W. J. & Dennis, E. S. FLC, a repressor of flowering, is regulated by genes in different inductive pathways: FLC protein levels and vernalization. Plant J. 29, 183–191 (2002).
Article PubMed CAS Google Scholar
Moon, J., Lee, H., Kim, M. & Lee, I. Analysis of flowering pathway integrators in Arabidopsis. Plant Cell Physiol. 46, 292–299 (2005).
Article PubMed CAS Google Scholar
Han, L. et al. A multi-omics integrative network map of maize. Nat. Genet 55, 144–153 (2023).
Article PubMed CAS Google Scholar
Lundberg, S. M., Erion, G. G. & Lee, S.-I. Consistent individualized feature attribution for tree ensembles. Preprint at https://doi.org/arXiv:1802.03888v3 (2019).
Aguirre, L., Hendelman, A., Hutton, S. F., McCandlish, D. M. & Lippman, Z. B. Idiosyncratic and dose-dependent epistasis drives variation in tomato fruit size. Science 382, 315–320 (2023).
Article ADS PubMed PubMed Central CAS Google Scholar
Richter, R. et al. Floral regulators FLC and SOC1 directly regulate expression of the B3-type transcription factor TARGET OF FLC AND SVP 1 at the Arabidopsis shoot apex via antagonistic chromatin modifications. PLoS Genet 15, e1008065 (2019).
Article PubMed PubMed Central CAS Google Scholar
Zhao, B., Xi, Y., Kim, J. & Sung, S. Chromatin architectural proteins regulate flowering time by precluding gene looping. Sci. Adv. 7, eabg3097 (2021).
Article ADS PubMed PubMed Central CAS Google Scholar
Ito, S., Song, Y. H. & Imaizumi, T. LOV domain-containing F-box proteins: light-dependent protein degradation modules in Arabidopsis. Mol. Plant 5, 573–582 (2012).
Article PubMed Google Scholar
Xu, X. M., Rose, A. & Meier, I. NUA activities at the plant nuclear pore. Plant Signal. Behav. 2, 553–555 (2007).
Article PubMed PubMed Central Google Scholar
He, Y. Chromatin regulation of flowering. Trends Plant Sci. 17, 556–562 (2012).
Article PubMed CAS Google Scholar
Bu, Z. et al. Regulation of Arabidopsis flowering by the histone mark readers MRG1/2 via interaction with CONSTANS to modulate FT expression. PLoS Genet 10, e1004617 (2014).
Article PubMed PubMed Central Google Scholar
Tian, H. et al. Photoperiod-responsive changes in chromatin accessibility in phloem companion and epidermis cells of Arabidopsis leaves. Plant Cell 33, 475–491 (2021).
Article PubMed PubMed Central Google Scholar
Genger, R. K., Peacock, J. W., Dennis, E. S. & Finnegan, J. E. Opposing effects of reduced DNA methylation on flowering time in Arabidopsis thaliana. Planta 216, 461–466 (2003).
Article PubMed CAS Google Scholar
Endelman, J. B. & Jannink, J.-L. Shrinkage estimation of the realized relationship matrix. G3 (Bethesda) 2, 1405–1413 (2012).
Article PubMed Google Scholar
Bradbury, P. J. et al. TASSEL: software for association mapping of complex traits in diverse samples. Bioinformatics 23, 2633–2635 (2007).
Article PubMed CAS Google Scholar
McCarthy, D. J., Campbell, K. R., Lun, A. T. L. & Wills, Q. F. Scater: pre-processing, quality control, normalization and visualization of single-cell RNA-seq data in R. Bioinformatics 33, 1179–1186 (2017).
Article PubMed PubMed Central CAS Google Scholar
Pedregosa, F. et al. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).
MathSciNet Google Scholar
Strobl, C., Boulesteix, A.-L. & Augustin, T. Unbiased split selection for classification trees based on the Gini Index. Comput. Stat. Data Anal. 52, 483–501 (2007).
Article MathSciNet Google Scholar
Wang, P. et al. Source data: Prediction of plant complex traits via integration of multi-omics data. figshare https://doi.org/10.6084/m9.figshare.26113933 (2024).
Wang, P. et al. Prediction of plant complex traits via integration of multi-omics data. https://github.com/ShiuLab/2024_Ath_GP. Zenodo https://doi.org/10.5281/ZENODO.12602565 (2024).

Download references

Acknowledgements

We thank Elyse Vischulis for help in data collection, and Chad Niederhuth and Sunil Kumar Kenchanmane Raju for helpful discussions on DNA methylation. We thank three reviewers for their valuable suggestions and comments that helped us to improve the quality of this manuscript. This work was supported by the U.S. Department of Energy Great Lakes Bioenergy Research Center (BER DE-SC0018409 to SHS), the National Science Foundation (DGE-1828149 and IOS-2218206 to S.H.S., K.S.A. and S.L.; IOS-2107215 and MCB-2210431 to M.D.L. and S.H.S.; DEB-1655630 to P.J.K.), the Scientific Research Foundation of and the Major Scientific Research Tasks from Kunpeng Institute of Modern Agriculture at Foshan (KIMAQD2022003 and KIMA-ZDKY2022004 to P.W.) and National Natural Science Foundation of China (32370241 to P.W.).

Author information

Authors and Affiliations

DOE Great Lakes Bioenergy Research Center, Michigan State University, East Lansing, MI, USA
Peipei Wang, Kenia Segura Abá & Shin-Han Shiu
Kunpeng Institute of Modern Agriculture at Foshan, Agricultural Genomics Institute at Shenzhen, Chinese Academy of Agricultural Sciences, Shenzhen, Guangdong, China
Peipei Wang
Department of Plant Biology, Michigan State University, East Lansing, MI, USA
Peipei Wang, Melissa D. Lehti-Shiu, Serena Lotreck & Shin-Han Shiu
Department of Computational Mathematics, Science, and Engineering, Michigan State University, East Lansing, MI, USA
Serena Lotreck & Shin-Han Shiu
Genetics and Genome Sciences Program, Michigan State University, East Lansing, MI, USA
Kenia Segura Abá & Shin-Han Shiu
Department of Plant and Agroecosystem Sciences, University of Wisconsin-Madison, Madison, WI, USA
Patrick J. Krysan

Authors

Peipei Wang
View author publications
You can also search for this author in PubMed Google Scholar
Melissa D. Lehti-Shiu
View author publications
You can also search for this author in PubMed Google Scholar
Serena Lotreck
View author publications
You can also search for this author in PubMed Google Scholar
Kenia Segura Abá
View author publications
You can also search for this author in PubMed Google Scholar
Patrick J. Krysan
View author publications
You can also search for this author in PubMed Google Scholar
Shin-Han Shiu
View author publications
You can also search for this author in PubMed Google Scholar

Contributions

P.W. and S.H.S. conceived and designed the study with input from S.L., K.S.A., and M.D.L.; P.W. and S.L. performed the methylation-related analysis; P.W. and K.S.A. analyzed the feature importance; P.J.K. created the gene mutants, and M.D.L. conducted the assessment of flowering time for loss-of-function mutant plants; P.W. conducted all other analyses. P.W., S.L., K.S.A., M.D.L., and S.H.S. wrote the paper. All authors read and approved the final manuscript.

Corresponding authors

Correspondence to Peipei Wang or Shin-Han Shiu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Maarten Koornneef and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Peer Review File

Description of Additional Supplementary Files

Supplementary Data 1

Supplementary Data 2

Supplementary Data 3

Supplementary Data 4

Supplementary Data 5

Supplementary Data 6

Supplementary Data 7

Supplementary Data 8

Supplementary Data 9

Supplementary Data 10

Supplementary Data 11

Supplementary Data 12

Supplementary Data 13

Supplementary Data 14

Supplementary Data 15

Supplementary Data 16

Supplementary Data 17

Supplementary Data 18

Supplementary Data 19

Supplementary Data 20

Reporting Summary

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Wang, P., Lehti-Shiu, M.D., Lotreck, S. et al. Prediction of plant complex traits via integration of multi-omics data. Nat Commun 15, 6856 (2024). https://doi.org/10.1038/s41467-024-50701-6

Download citation

Received: 19 November 2023
Accepted: 18 July 2024
Published: 10 August 2024
DOI: https://doi.org/10.1038/s41467-024-50701-6