Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 1998 Oct 13;95(21):12390-7.
doi: 10.1073/pnas.95.21.12390.

The optimization principle in phylogenetic analysis tends to give incorrect topologies when the number of nucleotides or amino acids used is small

M Nei  1 , S Kumar, K Takahashi
Affiliations

The optimization principle in phylogenetic analysis tends to give incorrect topologies when the number of nucleotides or amino acids used is small

M Nei et al. Proc Natl Acad Sci U S A. .

Abstract

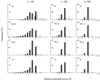
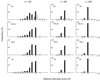
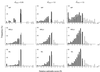
In the maximum parsimony (MP) and minimum evolution (ME) methods of phylogenetic inference, evolutionary trees are constructed by searching for the topology that shows the minimum number of mutational changes required (M) and the smallest sum of branch lengths (S), respectively, whereas in the maximum likelihood (ML) method the topology showing the highest maximum likelihood (A) of observing a given data set is chosen. However, the theoretical basis of the optimization principle remains unclear. We therefore examined the relationships of M, S, and A for the MP, ME, and ML trees with those for the true tree by using computer simulation. The results show that M and S are generally greater for the true tree than for the MP and ME trees when the number of nucleotides examined (n) is relatively small, whereas A is generally lower for the true tree than for the ML tree. This finding indicates that the optimization principle tends to give incorrect topologies when n is small. To deal with this disturbing property of the optimization principle, we suggest that more attention should be given to testing the statistical reliability of an estimated tree rather than to finding the optimal tree with excessive efforts. When a reliability test is conducted, simplified MP, ME, and ML algorithms such as the neighbor-joining method generally give conclusions about phylogenetic inference very similar to those obtained by the more extensive tree search algorithms.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Model trees used for computer simulation. Trees A, C, and D represent cases of constant rate of evolution, and tree B represents a case of varying rate of evolution. Trees D1 and D2 are incorrect topologies reconstructed from simulated sequences by using model tree D. Branch lengths for model trees are expressed in terms of the expected number of nucleotide substitutions per site. Values of a were determined from the pairwise distances between the two most distantly related sequences (dmax).
Figure 2
Figure 2
Distributions of relative optimality scores (R) of the MP, ME, and ML trees inferred by the exhaustive search (solid bars) and the single-tree search (open bars) algorithms. These results were obtained from 500 replications of computer simulation following model tree A in Fig. 1 with dmax = 1.0. n represents the number of nucleotides used. ME(JC) and ME(p) refer to ME trees with the Jukes–Cantor distance and the p-distance, respectively. R values for MP and ME (or NJ) trees are multiplied by c = 100, whereas those for ML trees are multiplied by c = 1,000. cR = 0 represents the case where the correct topology was obtained. Except for cR = 0, cR = x represents the cR values in the range of x − 1 < cR ≤ x for a positive integer x and in the range of x ≤ cR < x + 1 for a negative integer x. Thus, cR = 1 represents the cR values between 0 and 1 excluding cR = 0, cR = 2 represents the cR values between 1 and 2 excluding cR = 1, and cR = −1 represents the cR values between −1 and 0 excluding 0. We used c = 1,000 for ML trees, because the scale of R for ML trees was much finer than that for MP and ME trees.
Figure 3
Figure 3
Distributions of relative optimality scores (R) of the trees obtained by the MP, ME, and ML methods (solid bars) and the single-tree algorithms (open bars) when model tree B with dmax = 1.0 was used. See the legend of Fig. 2 for details.
Figure 4
Figure 4
Distributions of relative optimality scores (R) of the trees obtained by the MP, ME, and ML methods (solid bars) and the single-tree algorithms (open bars) when model tree C with n = 300 was used. When dmax = 1.5, the Jukes–Cantor distance was often undefinable so that p-distance was used. See the legend of Fig. 2 for details.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Eck R V, Dayhoff M O. Atlas of Protein Sequence and Structure. Silver Spring, MD: National Biomedical Research Foundation; 1966.
    1. Fitch W M. Syst Zool. 1971;20:406–416.
    1. Sober E. Reconstructing the Past: Parsimony, Evolution, and Inference. Cambridge, MA: MIT Press; 1988.
    1. Edwards A W F, Cavalli-Sforza L L. Heredity. 1963;18:553. (abstr.).
    1. Saitou N, Imanishi M. Mol Biol Evol. 1989;6:514–525.

Publication types

LinkOut - more resources