Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Comparative Study
. 2020 Nov 1;37(11):3292-3307.
doi: 10.1093/molbev/msaa139.

ASTRAL-Pro: Quartet-Based Species-Tree Inference despite Paralogy

Chao Zhang  1 , Celine Scornavacca  2 , Erin K Molloy  3 , Siavash Mirarab  4
Affiliations
Comparative Study

ASTRAL-Pro: Quartet-Based Species-Tree Inference despite Paralogy

Chao Zhang et al. Mol Biol Evol. .

Erratum in

Abstract

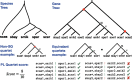
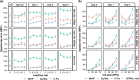
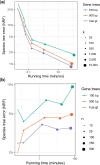
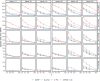
Phylogenetic inference from genome-wide data (phylogenomics) has revolutionized the study of evolution because it enables accounting for discordance among evolutionary histories across the genome. To this end, summary methods have been developed to allow accurate and scalable inference of species trees from gene trees. However, most of these methods, including the widely used ASTRAL, can only handle single-copy gene trees and do not attempt to model gene duplication and gene loss. As a result, most phylogenomic studies have focused on single-copy genes and have discarded large parts of the data. Here, we first propose a measure of quartet similarity between single-copy and multicopy trees that accounts for orthology and paralogy. We then introduce a method called ASTRAL-Pro (ASTRAL for PaRalogs and Orthologs) to find the species tree that optimizes our quartet similarity measure using dynamic programing. By studying its performance on an extensive collection of simulated data sets and on real data sets, we show that ASTRAL-Pro is more accurate than alternative methods.

Keywords: gene duplication and loss; incomplete lineage sorting; species-tree inference.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
Per-locus quartet score. Example gene family tree from the fungi data set (Butler et al. 2009) restricted to five species and a potential species tree. Two nodes of the gene tree are tagged as duplication (red dots) and others as speciation. Quartet scas1, sbay1 | smik1, scer1 is anchored by nodes u and v, where u is the anchor LCA. Because the LCAs of any three leaves (u or v) are speciation nodes, this quartet is a SQ. Quartet scas1, sbay2 | smik1, scer1 is anchored by node v and a duplication (top red dot). Since the duplication node is the LCA of three leaves, this quartet is a non-SQ that does not count toward the per-Locus (PL) quartet score. Note u is the anchor LCA of both scas1, sbay1 | smik1, scer1 and scas2, sbay1 | smik1, scer1; thus, they form the equivalence class scas*, sbay1 | smik1, scer1. In this example, there are ten equivalence classes of SQ quartets, eight of which match the species tree; thus, the PL quartet similarity is 8. The goal of ASTRAL-Pro is to find the species tree that maximizes this score summed over all input trees.
Fig. 2.
Fig. 2.
Species tree error on the S25 data set for n = 25 ingroup species, k = 1,000 gene trees, and both true and estimated gene trees from 100 and 500 bp alignments. (a) Controlling duplication rate (box columns; labeled by C) and the loss rate (x-axis; ratio of the loss rate to duplication rate). (b) Controlling the duplication rate (columns; labeled by C) and the ILS level (x-axis; NRF between true gene trees and the species tree for λ+=0). A-Pro and ASTRAL-multi are identical with λ+=0. See table 1 for parameters and supplementary figure S7, Supplementary Material online, for iGTP-DupLoss.
Fig. 3.
Fig. 3.
Accuracy (y-axis) and running time (x-axis) of A-Pro as the number of genes k (a) or the number of species n (b) changes. Both axes are in log-scale. As k increases, accuracy increases (see also supplementary figure S9, Supplementary Material online).
Fig. 4.
Fig. 4.
Species tree error on S100 data set. We compare the species tree error of the four methods, showing mean and standard error over ten replicates for each model condition, with varying numbers of genes (k) and sequence lengths (with Inf signifying true gene trees). Model conditions are labeled as a/b where a is the level of ILS (1 or 5) and b is the duplication/loss rate (1, 2, or 5).
Fig. 5.
Fig. 5.
Biological data set. (a) Plant data set (1kp). Right: ASTRAL on 424 single-copy gene trees. Left: ASTRAL-Pro on 9,683 multicopy gene trees. Three genomes (noted by * and dashed lines) were present in multicopy data set but not in the single-copy data. The single-copy tree includes 23 species that were not in the multicopy data and are pruned from the species tree (localPP support is recomputed using gene trees pruned to the 80 common species). Five branches (red) differ between the two trees. LocalPP support shown except when equal to 1. For the main highly supported conflict (Gnetifer vs. Gnepine), we show quartet support of alternative topologies among single-copy gene trees using DiscoVista (Sayyari et al. 2018). (b) Fungi data set. Right: Concatenation of 706 single-copy gene trees with the red branch enforced as a constraint (Butler et al. 2009). Left: ASTRAL-Pro on 7,280 multicopy gene trees.
Fig. 6.
Fig. 6.
Accuracy of the estimated species tree (y-axis) versus the number of single-copy genes (x-axis) across all 50 replicates of the S25 data set with k = 10,000 gene trees (from the experiment varying k). The “Multicopy” line, representing A-Pro, is using all gene trees, whereas the “Single-copy” line, representing ASTRAL, is only using the single-copy gene trees.
Fig. 7.
Fig. 7.
(1) An example of a quartet Q={a,b,c,d} with (a) unbalanced topology (Q ∠ G) and (b) balanced topology (Q⊥G). Anchors are u and v, and w is the anchor LCA. Although w has to be a speciation for Q to be considered a SQ, u and v (when different from w) can be either speciation or duplication. (2) An example of equivalence classes. Three equivalence classes are anchored on z: all eight quartets of the form {ai,bj,dk,e3}, of the form {ai,cj,dk,e3}, and of the form {bi,cj,dk,e3}, all with balanced topology. Anchored on x: two equivalence classes with unbalanced topology: {a1,b1,c1,d1}∼{a1,b1,c1,d3} and {a1,b1,c1,e3}. Anchored on y: two equivalence classes: {a2,b2,c2,d1}∼{a2,b2,c2,d3} and {a2,b2,c2,e3}.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. An J, Zhu L, Zhang Y, Tang H.. 2013. Efficient visible light photo-fenton-like degradation of organic pollutants using in situ surface-modified BiFeO3 as a catalyst. J Environ Sci (China )25(6):1213–1225. - PubMed
    1. Arvestad L, Berglund A-C, Lagergren J, Sennblad B.. 2004. Gene tree reconstruction and orthology analysis based on an integrated model for duplications and sequence evolution. In: Proceedings of the eighth annual international conference on computational molecular biology—RECOMB ’04; New York: ACM Press. p. 326–335.
    1. Arvestad L, Lagergren J, Sennblad B.. 2009. The gene evolution model and computing its associated probabilities. J ACM 56(2):1–44.
    1. Ballesteros JA, Hormiga G.. 2016. A new orthology assessment method for phylogenomic data: unrooted phylogenetic orthology. Mol Biol Evol. 33(8):2117–2134. - PubMed
    1. Ballesteros JA, Sharma PP.. 2019. A critical appraisal of the placement of Xiphosura (Chelicerata) with account of known sources of phylogenetic error. Syst Biol. 68(6):896–862. - PubMed

Publication types