Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Sep 12;15(9):e1007305.
doi: 10.1371/journal.pcbi.1007305. eCollection 2019 Sep.

Long-term dynamics of measles in London: Titrating the impact of wars, the 1918 pandemic, and vaccination

Alexander D Becker  1 , Amy Wesolowski  2 , Ottar N Bjørnstad  3   4 , Bryan T Grenfell  1   4   5
Affiliations

Long-term dynamics of measles in London: Titrating the impact of wars, the 1918 pandemic, and vaccination

Alexander D Becker et al. PLoS Comput Biol. .

Abstract

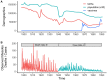
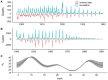
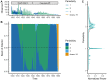
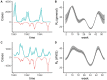
A key question in ecology is the relative impact of internal nonlinear dynamics and external perturbations on the long-term trajectories of natural systems. Measles has been analyzed extensively as a paradigm for consumer-resource dynamics due to the oscillatory nature of the host-pathogen life cycle, the abundance of rich data to test theory, and public health relevance. The dynamics of measles in London, in particular, has acted as a prototypical test bed for such analysis using incidence data from the pre-vaccination era (1944-1967). However, during this timeframe there were few external large-scale perturbations, limiting an assessment of the relative impact of internal and extra demographic perturbations to the host population. Here, we extended the previous London analyses to include nearly a century of data that also contains four major demographic changes: the First and Second World Wars, the 1918 influenza pandemic, and the start of a measles mass vaccination program. By combining mortality and incidence data using particle filtering methods, we show that a simple stochastic epidemic model, with minimal historical specifications, can capture the nearly 100 years of dynamics including changes caused by each of the major perturbations. We show that the majority of dynamic changes are explainable by the internal nonlinear dynamics of the system, tuned by demographic changes. In addition, the 1918 influenza pandemic and World War II acted as extra perturbations to this basic epidemic oscillator. Our analysis underlines that long-term ecological and epidemiological dynamics can follow very simple rules, even in a non-stationary population subject to significant perturbations and major secular changes.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. The demographic, vaccination, and measles data analyzed.
A) The observed population dynamics shown on a yearly scale. The major demographic fluctuations to births (red) and population counts (green) caused by WWII can be seen starting in 1940. B) Measles dynamics for London 1897–1991, shown on a weekly time scale with mortality (red) until 1940, and incidence (blue) through 1990. Note the case data are shown on a square root scale. Unscaled data are shown (inverted) in Fig 2.
Fig 2
Fig 2. The comparison of predicted against observed weekly measles dynamics for London 1897–1991.
A) The 75% quantile fit (blue ribbon) from the forward-simulated fitted model against the inverted death data (red) from 1897 to 1940 while B) shows the fit against the case data from 1940 through 1990. Note that although different data sources are used, the simulation shown here is a fully forward prediction starting in 1897. C) The inferred annual transmission pattern, shown in solid black. The mean yearly transmission rate here is 29. Confidence intervals (95% calculated using the chi-square approximation of the likelihood ratio test) on the inferred seasonality pattern are shown in shaded gray.
Fig 3
Fig 3. A comparison of predicted against observed measles dynamics for London 1897–1991 based on periodicity inferred from wavelet analysis.
A) The observed measles dynamics (death data: 1897–1940, case data: 1940–1991 shown on a square root scale) color coded by the dominant periodicity (in years). B) The density of attractor basins via the simulated stochastic model fitted to the data, also color coded temporally by dominant periodicity. C) The global power spectra of the data (red) against the simulated stochastic model calibrated against the data (blue). Periodicity for all figures is in years (e.g. periodicity 1 in A) and B) refers to annual dynamics). Note, that each simulation shown here is a forward simulation starting from 1897. This figure style is adapted from [12].
Fig 4
Fig 4. A comparison of predicted against observed measles dynamics for the subsetted WWII time period (1940 to 1946).
A) The predicted dynamics using the fitted model against the whole time series with the same visual fit information as Fig 2. B) The inferred seasonality across the whole-time series with mean R0 = 29. C) The predicted dynamics fit to just the WWII time period with the inferred seasonality in D). D) The inferred seasonality in just the WWII time period with average R0 = 33. Note the local WWII fit produces a lower amplitude seasonality pattern. In both B) and D) 95% confidence intervals (calculated using the chi-square approximation of the likelihood ratio test) on the inferred seasonality pattern are shown in shaded gray, while the inferred values are shown in solid black. Note that the seasonality pattern in D) yields a stronger fit the data while maintaining a generally lower amplitude.
Fig 5
Fig 5. A comparison of predicted against observed measles Lyapunov exponents for two biennial attractors.
A) Local Lyapunov exponents (LLEs) across the 1920–1935 biennial attractor predicted for mean birth rates. The filled blue circles indicate positive values with red indicating negative values. The size of the circle corresponds to the absolute value of the exponent. B) The observed LLEs across the 1920–1935 range using the true birth rates. C) Predicted LLE for the 1950–1965 biennial attractor using mean birth rates. D) Observed LLEs for the 1950–1965 data using the true birth rates.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Bjørnstad ON, Grenfell BT. Noisy clockwork: time series analysis of population fluctuations in animals. Science. 2001;293: 638–43. 10.1126/science.1062226 - DOI - PubMed
    1. Liu W, Hethcote HW, Levin SA. Dynamical behavior of epidemiological models with nonlinear incidence rates. J Math Biol. 1987;25: 359–380. 10.1007/BF00277162 - DOI - PubMed
    1. Olsen LF, Truty GL, Schaffer WM. Oscillations and chaos in epidemics: A nonlinear dynamic study of six childhood diseases in Copenhagen, Denmark. Theor Popul Biol. 1988;33: 344–370. 10.1016/0040-5809(88)90019-6 - DOI - PubMed
    1. Rohani P, Green CJ, Mantilla-Beniers NB, Grenfell BT. Ecological interference between fatal diseases. Nature. 2003;422: 885–888. 10.1038/nature01542 - DOI - PubMed
    1. Dalziel BD, Bjørnstad ON, van Panhuis WG, Burke DS, Metcalf CJE, Grenfell BT. Persistent Chaos of Measles Epidemics in the Prevaccination United States Caused by a Small Change in Seasonal Transmission Patterns. Ferguson NM, editor. PLOS Comput Biol. 2016;12: e1004655 10.1371/journal.pcbi.1004655 - DOI - PMC - PubMed

Publication types