Combining Graphical and Analytical Methods with Molecular Simulations To Analyze Time-Resolved FRET Measurements of Labeled Macromolecules Accurately
- PMID: 28709377
- PMCID: PMC5592652
- DOI: 10.1021/acs.jpcb.7b03441
Combining Graphical and Analytical Methods with Molecular Simulations To Analyze Time-Resolved FRET Measurements of Labeled Macromolecules Accurately
Abstract
Förster resonance energy transfer (FRET) measurements from a donor, D, to an acceptor, A, fluorophore are frequently used in vitro and in live cells to reveal information on the structure and dynamics of DA labeled macromolecules. Accurate descriptions of FRET measurements by molecular models are complicated because the fluorophores are usually coupled to the macromolecule via flexible long linkers allowing for diffusional exchange between multiple states with different fluorescence properties caused by distinct environmental quenching, dye mobilities, and variable DA distances. It is often assumed for the analysis of fluorescence intensity decays that DA distances and D quenching are uncorrelated (homogeneous quenching by FRET) and that the exchange between distinct fluorophore states is slow (quasistatic). This allows us to introduce the FRET-induced donor decay, εD(t), a function solely depending on the species fraction distribution of the rate constants of energy transfer by FRET, for a convenient joint analysis of fluorescence decays of FRET and reference samples by integrated graphical and analytical procedures. Additionally, we developed a simulation toolkit to model dye diffusion, fluorescence quenching by the protein surface, and FRET. A benchmark study with simulated fluorescence decays of 500 protein structures demonstrates that the quasistatic homogeneous model works very well and recovers for single conformations the average DA distances with an accuracy of < 2%. For more complex cases, where proteins adopt multiple conformations with significantly different dye environments (heterogeneous case), we introduce a general analysis framework and evaluate its power in resolving heterogeneities in DA distances. The developed fast simulation methods, relying on Brownian dynamics of a coarse-grained dye in its sterically accessible volume, allow us to incorporate structural information in the decay analysis for heterogeneous cases by relating dye states with protein conformations to pave the way for fluorescence and FRET-based dynamic structural biology. Finally, we present theories and simulations to assess the accuracy and precision of steady-state and time-resolved FRET measurements in resolving DA distances on the single-molecule and ensemble level and provide a rigorous framework for estimating approximation, systematic, and statistical errors.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
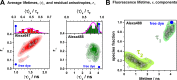
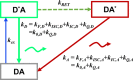

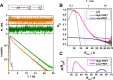




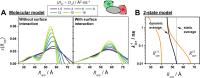


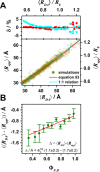
 and
and  , fluorescence
lifetime τD(0) = 4 ns, and a time-window of 12.5τD(0). (A) Relative
standard error δ per 106 photons of the distances
, fluorescence
lifetime τD(0) = 4 ns, and a time-window of 12.5τD(0). (A) Relative
standard error δ per 106 photons of the distances  (blue, left),
(blue, left),  (green, middle),
and their difference ΔRDA (red,
right). White lines are isolines
δ = 0.5 (also shown at panel D). (B) Isolines of δ(
(green, middle),
and their difference ΔRDA (red,
right). White lines are isolines
δ = 0.5 (also shown at panel D). (B) Isolines of δ( )) = 0.5 (blue line), δ(
)) = 0.5 (blue line), δ( ) = 0.5 (green
line), and δ(ΔRDA)=0.5 (red
line) for 106 counted photons (the same as white lines
at panel A). The isolines
partition the parameter space in four regions: (i) All three parameters
are resolved. (ii) The distances
) = 0.5 (green
line), and δ(ΔRDA)=0.5 (red
line) for 106 counted photons (the same as white lines
at panel A). The isolines
partition the parameter space in four regions: (i) All three parameters
are resolved. (ii) The distances  ,
,  can be reliably
determined while the relative
standard error of their difference δ(ΔRDA) increases above value 0.5. (iii) Only the shorter
distance
can be reliably
determined while the relative
standard error of their difference δ(ΔRDA) increases above value 0.5. (iii) Only the shorter
distance  is reliably estimated. The distance distribution
is only partially resolved, and the species with small FRET rate constant
cannot be distinguished from non-FRET species. (iv) None of the parameters
is resolved. The vertical lines indicate limiting distances
is reliably estimated. The distance distribution
is only partially resolved, and the species with small FRET rate constant
cannot be distinguished from non-FRET species. (iv) None of the parameters
is resolved. The vertical lines indicate limiting distances  of the region
i (red) and
of the region
i (red) and  of the region
ii (green). (C) Dependence
of the limiting distances
of the region
ii (green). (C) Dependence
of the limiting distances  and
and  on the number of detected photons.
on the number of detected photons.
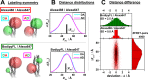
 . (B, left) The 2D probability distribution
function (counterfeit normal) of observed estimates of parameters
. (B, left) The 2D probability distribution
function (counterfeit normal) of observed estimates of parameters  ,
,  for expectations
for expectations  ,
,  . (B, right) The marginal (1D projections)
probability distribution functions of estimations of
. (B, right) The marginal (1D projections)
probability distribution functions of estimations of  (blue),
(blue),  (green),
and the probability distribution
functions of ΔRDA estimation (red,
shifted for comparison) for 4 sets of expected parameters marked by
circles in Figure 14A,B and here in panel A. Indices (i, ii, iii) correspond to the regions
defined in Figure 14B.
(green),
and the probability distribution
functions of ΔRDA estimation (red,
shifted for comparison) for 4 sets of expected parameters marked by
circles in Figure 14A,B and here in panel A. Indices (i, ii, iii) correspond to the regions
defined in Figure 14B.Similar articles
-
Accurate distance determination of nucleic acids via Förster resonance energy transfer: implications of dye linker length and rigidity.J Am Chem Soc. 2011 Mar 2;133(8):2463-80. doi: 10.1021/ja105725e. Epub 2011 Feb 3. J Am Chem Soc. 2011. PMID: 21291253
-
Fluorescence resonance energy transfer (FRET) and competing processes in donor-acceptor substituted DNA strands: a comparative study of ensemble and single-molecule data.J Biotechnol. 2002 Jan;82(3):211-31. doi: 10.1016/s1389-0352(01)00039-3. J Biotechnol. 2002. PMID: 11999691 Review.
-
Contribution of fluorophore dynamics and solvation to resonant energy transfer in protein-DNA complexes: a molecular-dynamics study.Biophys J. 2014 Aug 5;107(3):700-710. doi: 10.1016/j.bpj.2014.06.023. Biophys J. 2014. PMID: 25099809 Free PMC article.
-
Complete Kinetic Theory of FRET.J Phys Chem B. 2018 Dec 13;122(49):11677-11694. doi: 10.1021/acs.jpcb.8b07719. Epub 2018 Oct 30. J Phys Chem B. 2018. PMID: 30351105
-
Imaging protein-protein interactions using fluorescence resonance energy transfer microscopy.Methods. 2001 Jul;24(3):289-96. doi: 10.1006/meth.2001.1189. Methods. 2001. PMID: 11403577 Review.
Cited by
-
Cross-validation of distance measurements in proteins by PELDOR/DEER and single-molecule FRET.Nat Commun. 2022 Jul 29;13(1):4396. doi: 10.1038/s41467-022-31945-6. Nat Commun. 2022. PMID: 35906222 Free PMC article.
-
Chromophoric Dendrimer-Based Materials: An Overview of Holistic-Integrated Molecular Systems for Fluorescence Resonance Energy Transfer (FRET) Phenomenon.Polymers (Basel). 2021 Dec 15;13(24):4404. doi: 10.3390/polym13244404. Polymers (Basel). 2021. PMID: 34960954 Free PMC article. Review.
-
FRET-based dynamic structural biology: Challenges, perspectives and an appeal for open-science practices.Elife. 2021 Mar 29;10:e60416. doi: 10.7554/eLife.60416. Elife. 2021. PMID: 33779550 Free PMC article. Review.
-
On the necessity of an integrative approach to understand protein structural dynamics.J Zhejiang Univ Sci B. 2019 Jun;20(6):496-502. doi: 10.1631/jzus.B1900135. J Zhejiang Univ Sci B. 2019. PMID: 31090275 Free PMC article. Review.
-
Reliability and accuracy of single-molecule FRET studies for characterization of structural dynamics and distances in proteins.Nat Methods. 2023 Apr;20(4):523-535. doi: 10.1038/s41592-023-01807-0. Epub 2023 Mar 27. Nat Methods. 2023. PMID: 36973549 Free PMC article.
References
-
- Förster T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 1948, 437, 55–75. 10.1002/andp.19484370105. - DOI
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

