Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Dec;73(4):1199-1209.
doi: 10.1111/biom.12676. Epub 2017 Feb 17.

A general statistical framework for subgroup identification and comparative treatment scoring

Shuai Chen  1 , Lu Tian  2 , Tianxi Cai  3 , Menggang Yu  1
Affiliations

A general statistical framework for subgroup identification and comparative treatment scoring

Shuai Chen et al. Biometrics. 2017 Dec.

Abstract

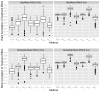
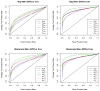
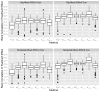
Many statistical methods have recently been developed for identifying subgroups of patients who may benefit from different available treatments. Compared with the traditional outcome-modeling approaches, these methods focus on modeling interactions between the treatments and covariates while by-pass or minimize modeling the main effects of covariates because the subgroup identification only depends on the sign of the interaction. However, these methods are scattered and often narrow in scope. In this article, we propose a general framework, by weighting and A-learning, for subgroup identification in both randomized clinical trials and observational studies. Our framework involves minimum modeling for the relationship between the outcome and covariates pertinent to the subgroup identification. Under the proposed framework, we may also estimate the magnitude of the interaction, which leads to the construction of scoring system measuring the individualized treatment effect. The proposed methods are quite flexible and include many recently proposed estimators as special cases. As a result, some estimators originally proposed for randomized clinical trials can be extended to observational studies, and procedures based on the weighting method can be converted to an A-learning method and vice versa. Our approaches also allow straightforward incorporation of regularization methods for high-dimensional data, as well as possible efficiency augmentation and generalization to multiple treatments. We examine the empirical performance of several procedures belonging to the proposed framework through extensive numerical studies.

Keywords: A-learning; Individualized treatment rules; Observational studies; Propensity score; Regularization.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Boxplots for the rank correlation coefficients between the estimated benefit scores and true treatment effects for continuous outcomes. Method “Full” uses the full regression; Method “Wsq–L” uses the weighting method with squared loss M(y, v) = (y − v)2 and a linear f ; Method “Wsq–A” uses the weighting method with squared loss M(y, v) = (y − v)2 and a nonparametric additive f ; Method “Wflo–L” uses the weighting method with flipping outcome-weighted logistic loss M(y, v) = |y| log[1 + exp{−sign(y)v}] and a linear f ; Method “Asq–L” uses the A-learning method with M(y, v) = (y − v)2 and a linear f ; Method “Asq–A” uses the A-learning method with M(y, v) = (y − v)2 and a nonparametric additive f ; Method “Aflo–L” uses the A-learning method with flipping outcome-weighted logistic loss M(y, v) = |y| log[1 + exp{−sign(y)v}] and a linear f.
Figure 2
Figure 2
ROC curves of estimated benefit scores for subgroup identification when the outcomes are continuous. Method “Full” uses the full regression; Method “Wsq–L” uses the weighting method with squared loss M(y, v) = (y−v)2 and a linear f ;Method “Wsq–A” uses the weighting method with squared loss M(y, v) = (y−v)2 and a nonparametric additive f ;Method “Wflo–L” uses the weighting method with flipping outcome-weighted logistic loss M(y, v) = |y| log[1 + exp{−sign(y)v}] and a linear f ; Method “Asq–L” uses the A-learning method with M(y, v) = (y − v)2 and a linear f ; Method “Asq–A” uses the A-learning method with M(y, v) = (y − v)2 and a nonparametric additive f ; Method “Aflo–L” uses the A-learning method with flipping outcome-weighted logistic loss M(y, v) = |y| log[1 + exp{−sign(y)v}] and a linear f.
Figure 3
Figure 3
Boxplots for the rank correlation coefficients between the estimated benefit scores and true treatment effects for binary outcomes. Method “Full” uses the full logistic regression; Method “Wlo–L” uses the weighting method with logistic loss M(y, v) = −[yv − log{1 + exp(v)}] and a linear f ; Method “Wlo–A” uses the weighting method with logistic loss M(y, v) = −[yv − log{1 + exp(v)}] and a nonparametric additive f ;Method “Wflo–L” uses the weighting method with flipping outcome weighted logistic loss M(y, v) = |y| log[1+exp{−sign(y)v}] and a linear f ;Method “Alo–L” uses the A-learning method with logistic loss M(y, v) = −[yv − log{1 + exp(v)}] and a linear f ; Method “Alo–A” uses the A-learning method with logistic loss M(y, v) = −[yv − log{1 + exp(v)}] and a nonparametric additive f ;Method “Aflo–L” uses the A-learning method with flipping outcome weighted logistic loss M(y, v) = |y| log[1 + exp{−sign(y)v}] and a linear f.
Figure 4
Figure 4
ROC curves of estimated benefit scores for subgroup identification when outcomes are binary. Method “Full” uses the full logistic regression; Method “Wlo–L” uses the weighting method with logistic loss M(y, v) = −[yv − log{1 + exp(v)}] and a linear f ; Method “Wlo–A” uses the weighting method with logistic loss M(y, v) = −[yv − log{1 + exp(v)}] and a nonparametric additive f ; Method “Wflo–L” uses the weighting method with flipping outcome-weighted logistic loss M(y, v) = |y| log[1 + exp{−sign(y)v}] and a linear f ; Method “Alo–L” uses the A-learning method with logistic loss M(y, v) = −[yv − log{1 + exp(v)}] and a linear f ; Method “Alo–A” uses the A-learning method with logistic loss M(y, v) = −[yv − log{1 + exp(v)}] and a nonparametric additive f ; Method “Aflo–L” uses the A-learning method with flipping outcome-weighted logistic loss M(y, v) = |y| log[1 + exp{−sign(y)v}] and a linear f.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Cai T, Tian L, Wong PH, Wei L. Analysis of randomized comparative clinical trial data for personalized treatment selections. Biostatistics. 2011;12:270–282. - PMC - PubMed
    1. Ciarleglio A, Petkova E, Ogden RT, Tarpey T. Treatment decisions based on scalar and functional baseline covariates. Biometrics. 2015;71:884–94. - PMC - PubMed
    1. Foster JC, Taylor JM, Ruberg SJ. Subgroup identification from randomized clinical trial data. Statistics in medicine. 2011;30:2867–2880. - PMC - PubMed
    1. Gabriel S, Normand S. Getting the methods right–the foundation of patient-centered outcomes research. N Engl J Med. 2012;367:787–90. - PubMed
    1. Hastie TJ, Tibshirani RJ, Friedman JH. Springer series in statistics. Springer; New York: 2009. The elements of statistical learning: data mining, inference, and prediction.

Publication types