Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 Jun;9(3):95-103.
doi: 10.1049/iet-syb.2014.0046.

Global stability of infection-free state and endemic infection state of a modified human immunodeficiency virus infection model

Qilin Sun  1 , Lequan Min  2 , Yang Kuang  3
Affiliations

Global stability of infection-free state and endemic infection state of a modified human immunodeficiency virus infection model

Qilin Sun et al. IET Syst Biol. 2015 Jun.

Abstract

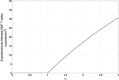
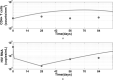
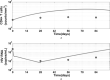
This study proposes a modified human immunodeficiency virus (HIV) infection differential equation model with a saturated infection rate. This model has an infection-free equilibrium point and an endemic infection equilibrium point. Using Lyapunov functions and LaSalle's invariance principle shows that if the model's basic reproductive number R0 < 1, the infection-free equilibrium point is globally asymptotically stable, otherwise the endemic infection equilibrium point is globally asymptotically stable. It is shown that a forward bifurcation will occur when R0 = 1. The basic reproductive number R0 of the modified model is independent of plasma total CD4⁺ T cell counts and thus the modified model is more reasonable than the original model proposed by Buonomo and Vargas-De-León. Based on the clinical data from HIV drug resistance database of Stanford University, using the proposed model simulates the dynamics of two group patients' anti-HIV infection treatments. The simulation results have shown that the first 4 weeks' treatments made the two group patients' R'0 < 1, respectively. After the period, drug resistance made the two group patients' R'0 > 1. The results explain why the two group patients' mean CD4⁺ T cell counts raised and mean HIV RNA levels declined in the first period, but contrary in the following weeks.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Forward bifurcation
Fig. 2
Fig. 2
Outcomes of the treatment efficacy of Group I; circles: clinical data; solid line: numerical simulation of (14) a Mean uninfected CD4+ T cell counts b Mean HIV RNA levels
Fig. 3
Fig. 3
Outcomes of the treatment efficacy of Group II; circles: clinical data; solid line: numerical simulation of (14) a Mean uninfected CD4+ T cell counts b Mean HIV RNA levels
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. ‘World Health Organization HIV/AIDS Key facts’, http://www.who.int/mediacentre/factsheets/fs360/en/index.html, accessed July 2014
    1. Nowak M.A. Bonhoeffer S. Shaw G.M., and May R.M.: ‘Anti‐viral drug treatment: Dynamics of resistance in free virus and infected cell populations’, J. Theor. Biol., 1997, 184, (2), pp. 203–217 (doi: 10.1006/jtbi.1996.0307) - DOI - PubMed
    1. Mittler J.E. Sulzer B. Neumann A.U., and Perelson A.S.: ‘Influence of delayed viral production on viral dynamics in HIV‐1 infected patients’, Math. Biosci., 1998, 152, (2), pp. 143–163 (doi: 10.1016/S0025-5564(98)10027-5) - DOI - PubMed
    1. Nowak M.A., and May R.M.: ‘Virus dynamics’ (Oxford University Press, 2000)
    1. Nelson P.W., and Perelson A.S.: ‘Mathematical analysis of delay differential equation models of HIV‐1 infection’, Math. Biosci., 2002, 179, (1), pp. 73–94 (doi: 10.1016/S0025-5564(02)00099-8) - DOI - PubMed

Publication types