Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2015 Dec:119:218-30.
doi: 10.1016/j.biochi.2014.12.007. Epub 2014 Dec 18.

Evolution, energy landscapes and the paradoxes of protein folding

Peter G Wolynes  1
Affiliations
Review

Evolution, energy landscapes and the paradoxes of protein folding

Peter G Wolynes. Biochimie. 2015 Dec.

Abstract

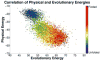
Protein folding has been viewed as a difficult problem of molecular self-organization. The search problem involved in folding however has been simplified through the evolution of folding energy landscapes that are funneled. The funnel hypothesis can be quantified using energy landscape theory based on the minimal frustration principle. Strong quantitative predictions that follow from energy landscape theory have been widely confirmed both through laboratory folding experiments and from detailed simulations. Energy landscape ideas also have allowed successful protein structure prediction algorithms to be developed. The selection constraint of having funneled folding landscapes has left its imprint on the sequences of existing protein structural families. Quantitative analysis of co-evolution patterns allows us to infer the statistical characteristics of the folding landscape. These turn out to be consistent with what has been obtained from laboratory physicochemical folding experiments signaling a beautiful confluence of genomics and chemical physics.

Keywords: Folding landscape; Natural selection; Structure prediction.

PubMed Disclaimer

Figures

Fig 1
Fig 1. The Funnel Diagram
A schematic diagram of the energy landscape of a protein, here illustrated with the PDZ domain whose native structure is shown at the bottom of the funnel. The energy landscape exists in a very high dimensional space. The diagram can only give a sense of this through its representation of two dimensions. The radial coordinate measures the configurational entropy which decreases as the protein takes on a more fully folded structure. The energy of individual configurations is represented by the vertical axis. The values of the energy indicated on this axis are strongly correlated with the fraction of native structures that has formed which is often measured by the fraction of correct native-like contacts called Q. Q also typically increases as the structures descend in the funnel. The energy and entropy oppose each other so that at high temperature the protein is found in an ensemble of states near the top of the funnel. Structures of denatured configurations thus are shown near the top of the funnel. At low temperature, in contrast, an ensemble clustered around the native structures becomes thermally occupied at the bottom of the funnel. The imperfect matching of entropy and energy leads typically to a free energy barrier that separates these two ensembles of states. Surmounting this barrier limits the folding rate. The small mini-funnels on the sides of the funnel represent trap states. These traps typically possess some native structure but also they contain energetically favorable alternative non-native contacts. Because the non-native contacts are not consistent with each other, rarely are such mini-funnels competitive in an energetic sense with the native basin. The stability of non-native interactions in any one of these traps is an unusual rare accident while the interactions that are formed in native structure have evolved in order for the individual natively folded structure to be especially stable.
Fig 2
Fig 2. The Distribution of Energies on a Funneled Folding Landscape
A schematic spectrum showing the density of states of a minimally frustrated protein. Compact alternative or decoy states are distributed with a nearly Gaussian distribution of energies through the random addition of conflicting contributions. At a temperature T, the thermally occupied decoys will be diminished in number but they will still have a Gaussian distribution of energies that is shifted downwards. At the glass temperature Tg only a very small number of such trap states would be thermally occupied. The energy Eg at Tg can be estimated from the width of the unbiased decoy distribution ΔE. For a minimally frustrated protein an evolved sequence fits the target structure quite well so that at a folding temperature TF the Boltzmann weight for the target structure competes with the entire collection of states in the unfolded ensemble. For most random heteropolymers no significant gap in the spectrum exists. As the extra stability of the target δEF increases, relative to the width of decoy distribution ΔE, the folded structure can be more and more easily picked out from the alternatives. By maximizing δEF/ΔE over a set of sequences one finds more and more stable “well-designed” sequences. Conversely if many sequence/structure pairs are known the parameters in the energy function can be varied so as to maximize the energy of δEF/ΔE for the set. The resulting energy function summarizes the structural sequence correlations in the training set. In this way structural data allow us to learn transferable energy functions. Energy landscape theory provides us a theoretical “license to do bioinformatics.”
Fig 3
Fig 3. Predictions of Globular Protein Tertiary Structure
A gallery of globular protein structures predicted by the AWSEM energy landscape optimized force field are shown overlapped with the correct x-ray structures. The agreement is comparable to what can be found via homology modeling but no homology information was used in making these predictions. The examples are 3ICB: vitamin D-dependent calcium-binding protein; 2MHR: myohemerythrin; 1JWE: N-terminal domain of E. coli DNAB helicase; 1R69: aminoterminal domain of phage 434 repressor; 256bB: cytochrome B562; 1utg: uteroglobin; 1MBA: aplysia limacina myoglobin; and 4CPV: carp parvalbuminCARP. For details please see Ref .
Fig 4
Fig 4. Predictions of Membrane Protein Structures
A gallery of membrane proteins structure predicted by the AWSEM-Membrane force field shown overlapped with the correct x-ray structures. The examples are 1IWG: subdomain of multidrug efux transporter; 1J4N: subdomain of aquaporin water channel AQP1; 1PV6: subdomain of lactose permease transporter; 1PY6SD: subdomain of bacteriorhodopsin; 1OCC: subdomain of cytochrome C oxidase aa3; 2RH1: 2-Adrenergic GPCR; 2BG9: subdomain of nicotinic acetylcholine receptor; and 2BL2: subdomain of V-type Na+-ATPase. For details please see Ref .
Fig 5
Fig 5. The Folding Super Landscape
The super-energy landscape of proteins is pictured here. Ideally this would be shown as a function of both sequence and conformation simultaneously. The large funnels are pictured as a function of sequence space with the radial sizes connoting sequence entropy. Energy is again the vertical axis. Natural proteins are not necessarily the lowest energy designs. These would be found at the bottom of the super funnel. For each target the configuration space landscape is funneled, but only to an energy EF. This structural energy landscape is, however, shown superimposed on the sequence space landscape. Disordered compact structures and sequence scrambled decoys have comparable energy statistics. They are shown near the top of the landscape. The funnels to other structures start from these same high energy states but again would finally reach energies near EF if they have sufficiently evolved under the minimal frustration selection constraint. The energy of the traps EG can be estimated by scrambling sequences within the native structure. This diagram shows how the evolutionary and physical configurational landscapes are related to each other. Notice that sequence space is cosmologically bigger than the structure space is as reflected by the large sequence entropy at EF. This excess coding space allows minimally frustrated landscapes to be found through the random processes of natural selection.
Fig 6
Fig 6. The Distributions of Energies in Sequence and Configuration Space
The schematic spectrum in sequence space is shown superimposed on the configurational energy spectrum. Notice that there are many sequences that fold to the same target structure because the selection temperature Tsel is greater than the sequence space glass transition temperature. This temperature in turn is lower than the structuralspace glass transition at Tg.
Fig 7
Fig 7. The Correlation between Physical and Evolutionary Folding Landscapes
We evaluate the energies, on using the physics based AWSEM energy function, the other using the direct contact approximation genomic based energy function both for scrambled sequences and for natural sequences in the 1r69 repressor family. These pairs of energies are then plotted. We see that both the physical and evolutionary energy landscapes have sizable gaps showing the minimally frustrated nature of the proteins. For details please see Ref .
Fig 8
Fig 8. The Correlation between the Evolutionary and Physical Folding Landscape
We evaluate the energies of structures using both a physical and a genomic energy function. The pairs shown in the figures correspond to partially folded protein structures generated via molecular simulation using the AWSEM energy function for the Ir69 family. Again the two landscapes turn out to be funneled and strongly correlated as would be expected from the minimal frustration principle. The colors of the points correspond to the fraction of native contacts formed in the sampled structure. For details please see Ref .
Fig 9
Fig 9. The Smoothness of the Folding Funnel Quantified by Coevolutionary Information
The Tf/Tg ratios for several protein families are inferred using genomics and landscape theory shown. The families are denoted by the PDB ID codes of the representative structures which are described in Ref . Tf/Tg measures the smoothness of a folding landscape. Higher values correspond to more ideal funnels. The red circle is an alternate way of making an estimate by comparing changes in evolutionary energies and experimentally measured stability changes. The estimated Tf/Tg ratios for all the natural protein families studied are larger than one so the folding landscape is confirmed to be a funnel. The estimates are clustered around the value of Tf/Tg = 2.5 that was estimated by Clementi and Plotkin through a comparison of measured Φ values with simulated ones. For details please see Ref .
Fig 10
Fig 10. Frustration Serves a Functional Purpose
A diagram showing the minimally frustrated web of interactions in two structural forms of – RhoA an allosteric protein. This web is indicated in green. The frustrated interactions in the regions shown in red lead to alternate nearly energetically degenerate configurations that allow these regions to function as hinges. The lower panel shows the frustration levels at different sequence locations, the red line indicating the number of frustrated contacts, green the number of minimally frustrated contacts. The black line indicates the local overlap of the two interconnecting structures. Notice the regions that move (and have low Q:) correspond to the most energetically frustrated regions. For details please see Ref .
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Wolynes PG. Three Paradoxes of Protein Folding. In: Bohr H, Brunak S, editors. Proceedings on Symposium on Protein Folds: A Distance-Based Approach, Symposium Distance-Based Approaches to Protein Structure Determination II; Copenhagen. November 1994; Boca Raton, FL: CRC Press; 1995. pp. 3–17.
    1. Anfinsen CB. Nobel Lecture. Bethesda, MD: National Institutes Of Health; Dec 11, 1972. Studies On The Principles That Govern The Folding Of Protein Chains. http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1972/anfinsen....
    1. Stent G. That was the molecular biology that was. Science. 1968;160:390–395. - PubMed
    1. Service RF. Problem -Solved* (*Sort of) Science. 2008;321:784–786. - PubMed
    1. Schafer NP, Kim BL, Zheng W, Wolynes PG. Learning to Fold Proteins Using Energy Landscape Theory. Isr J Chem. 2013;53:1–28. - PMC - PubMed

Publication types

LinkOut - more resources