Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Jun;1(2):115-130.
doi: 10.1007/s40484-013-0012-4.

Modeling the specificity of protein-DNA interactions

Gary D Stormo

Modeling the specificity of protein-DNA interactions

Gary D Stormo. Quant Biol. 2013 Jun.

Abstract

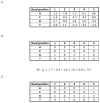
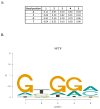
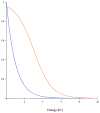
The specificity of protein-DNA interactions is most commonly modeled using position weight matrices (PWMs). First introduced in 1982, they have been adapted to many new types of data and many different approaches have been developed to determine the parameters of the PWM. New high-throughput technologies provide a large amount of data rapidly and offer an unprecedented opportunity to determine accurately the specificities of many transcription factors (TFs). But taking full advantage of the new data requires advanced algorithms that take into account the biophysical processes involved in generating the data. The new large datasets can also aid in determining when the PWM model is inadequate and must be extended to provide accurate predictions of binding sites. This article provides a general mathematical description of a PWM and how it is used to score potential binding sites, a brief history of the approaches that have been developed and the types of data that are used with an emphasis on algorithms that we have developed for analyzing high-throughput datasets from several new technologies. It also describes extensions that can be added when the simple PWM model is inadequate and further enhancements that may be necessary. It briefly describes some applications of PWMs in the discovery and modeling of in vivo regulatory networks.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Weight matrices and sequence encoding. A. The weight matrix for a hypothetical transcription factor (YFTF). Scores are provided for each possible base at each position in a five-long binding site. B. The encoding of a particular sequence, GCGGA, with a 1 for the base that occurs at each position and all other elements are 0. The score of the sequence, given the matrix in part A, is shown. C. An alternative weight matrix for the consensus sequence GCGRM (R=A or T, M=A or C). Any sequence that matches the consensus will get a score of 5, allowing one mismatch requires a score of at least 4, etc. This shows how any consensus sequence can be converted into an equivalent weight matrix that will return exactly the same set of sites.
Figure 2
Figure 2
Position frequency matrix (PFM) and information content logo. A. The position frequency matrix (PFM) for the YFTF log-odds matrix from Figure 1A. The sum of the base frequencies for each position is 1. B. An information content logo for YFTF based on the PFM of part A. The height of the column at each position is the information content (IC) and the individual base heights are in proportion to their frequencies.
Figure 3
Figure 3
Binding Probabilities as a function of binding energy. Blue line is the relative binding probability, compared to the consensus sequence (with E=0), for sequences with energy on the X-axis. Red line is the absolute binding probability under conditions where the consensus is about 95% bound (μ = 2).
Figure 4
Figure 4
Energy modeling. A. The energy matrix for YFTF. The average energy at each position is defined as 0 in this matrix, and bases with negative values are preferred, and those with positive values are discriminated against, compared to the average. B. An energy logo showing the energies of each base at each position, with an average of 0 as in the matrix of part A. Note that the Y-axis is −E, so the preferred bases are on top. C. The PFM for binding sites under conditions where the preferred sequence is 95% bound. D. The log-odds matrix based on the PFM of part C (assuming an equal frequency background). F. The information content logo for the PFM of part C.
Figure 4
Figure 4
Energy modeling. A. The energy matrix for YFTF. The average energy at each position is defined as 0 in this matrix, and bases with negative values are preferred, and those with positive values are discriminated against, compared to the average. B. An energy logo showing the energies of each base at each position, with an average of 0 as in the matrix of part A. Note that the Y-axis is −E, so the preferred bases are on top. C. The PFM for binding sites under conditions where the preferred sequence is 95% bound. D. The log-odds matrix based on the PFM of part C (assuming an equal frequency background). F. The information content logo for the PFM of part C.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Stormo GD, Schneider TD, Gold L, Ehrenfeucht A. Use of the ‘Perceptron’ algorithm to distinguish translational initiation sites in E. coli. Nucleic acids research. 1982;10:2997–3011. - PMC - PubMed
    1. Benos PV, Lapedes AS, Stormo GD. Probabilistic code for DNA recognition by proteins of the EGR family. Journal of molecular biology. 2002;323:701–727. - PubMed
    1. Kaplan T, Friedman N, Margalit H. Ab initio prediction of transcription factor targets using structural knowledge. PLoS computational biology. 2005;1:e1. - PMC - PubMed
    1. Wolfe SA, Nekludova L, Pabo CO. DNA recognition by Cys2His2 zinc finger proteins. Annual review of biophysics and biomolecular structure. 2000;29:183–212. - PubMed
    1. Klug A. The discovery of zinc fingers and their development for practical applications in gene regulation and genome manipulation. Quarterly reviews of biophysics. 2010;43:1–21. - PubMed