Probabilistic PCA of censored data: accounting for uncertainties in the visualization of high-throughput single-cell qPCR data
- PMID: 24618470
- PMCID: PMC4071202
- DOI: 10.1093/bioinformatics/btu134
Probabilistic PCA of censored data: accounting for uncertainties in the visualization of high-throughput single-cell qPCR data
Abstract
Motivation: High-throughput single-cell quantitative real-time polymerase chain reaction (qPCR) is a promising technique allowing for new insights in complex cellular processes. However, the PCR reaction can be detected only up to a certain detection limit, whereas failed reactions could be due to low or absent expression, and the true expression level is unknown. Because this censoring can occur for high proportions of the data, it is one of the main challenges when dealing with single-cell qPCR data. Principal component analysis (PCA) is an important tool for visualizing the structure of high-dimensional data as well as for identifying subpopulations of cells. However, to date it is not clear how to perform a PCA of censored data. We present a probabilistic approach that accounts for the censoring and evaluate it for two typical datasets containing single-cell qPCR data.
Results: We use the Gaussian process latent variable model framework to account for censoring by introducing an appropriate noise model and allowing a different kernel for each dimension. We evaluate this new approach for two typical qPCR datasets (of mouse embryonic stem cells and blood stem/progenitor cells, respectively) by performing linear and non-linear probabilistic PCA. Taking the censoring into account results in a 2D representation of the data, which better reflects its known structure: in both datasets, our new approach results in a better separation of known cell types and is able to reveal subpopulations in one dataset that could not be resolved using standard PCA.
Availability and implementation: The implementation was based on the existing Gaussian process latent variable model toolbox (https://github.com/SheffieldML/GPmat); extensions for noise models and kernels accounting for censoring are available at http://icb.helmholtz-muenchen.de/censgplvm.
© The Author 2014. Published by Oxford University Press. All rights reserved.
Figures
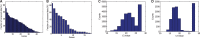

 (B)
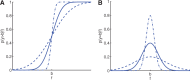
(B)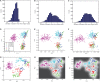

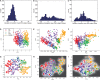
Similar articles
-
Diffusion maps for high-dimensional single-cell analysis of differentiation data.Bioinformatics. 2015 Sep 15;31(18):2989-98. doi: 10.1093/bioinformatics/btv325. Epub 2015 May 21. Bioinformatics. 2015. PMID: 26002886
-
A novel approach for resolving differences in single-cell gene expression patterns from zygote to blastocyst.Bioinformatics. 2012 Sep 15;28(18):i626-i632. doi: 10.1093/bioinformatics/bts385. Bioinformatics. 2012. PMID: 22962491 Free PMC article.
-
Probabilistic count matrix factorization for single cell expression data analysis.Bioinformatics. 2019 Oct 15;35(20):4011-4019. doi: 10.1093/bioinformatics/btz177. Bioinformatics. 2019. PMID: 30865271
-
Applying stability selection to consistently estimate sparse principal components in high-dimensional molecular data.Bioinformatics. 2015 Aug 15;31(16):2683-90. doi: 10.1093/bioinformatics/btv197. Epub 2015 Apr 10. Bioinformatics. 2015. PMID: 25861969 Free PMC article.
-
Estimation of low quantity genes: a hierarchical model for analyzing censored quantitative real-time PCR data.PLoS One. 2013 May 31;8(5):e64900. doi: 10.1371/journal.pone.0064900. Print 2013. PLoS One. 2013. PMID: 23741414 Free PMC article.
Cited by
-
qRT-PCR evaluation of the transcriptional response of zebra mussel to heavy metals.BMC Genomics. 2015 May 6;16(1):354. doi: 10.1186/s12864-015-1567-4. BMC Genomics. 2015. PMID: 25943386 Free PMC article.
-
MISC: missing imputation for single-cell RNA sequencing data.BMC Syst Biol. 2018 Dec 14;12(Suppl 7):114. doi: 10.1186/s12918-018-0638-y. BMC Syst Biol. 2018. PMID: 30547798 Free PMC article.
-
Single-cell gene expression profiling and cell state dynamics: collecting data, correlating data points and connecting the dots.Curr Opin Biotechnol. 2016 Jun;39:207-214. doi: 10.1016/j.copbio.2016.04.015. Epub 2016 May 23. Curr Opin Biotechnol. 2016. PMID: 27152696 Free PMC article. Review.
-
Revealing the vectors of cellular identity with single-cell genomics.Nat Biotechnol. 2016 Nov 8;34(11):1145-1160. doi: 10.1038/nbt.3711. Nat Biotechnol. 2016. PMID: 27824854 Free PMC article. Review.
-
Dimension Reduction and Clustering Models for Single-Cell RNA Sequencing Data: A Comparative Study.Int J Mol Sci. 2020 Mar 22;21(6):2181. doi: 10.3390/ijms21062181. Int J Mol Sci. 2020. PMID: 32235704 Free PMC article.
References
-
- Bishop CM. Pattern Recognition and Machine Learning (Information Science and Statistics) New York: Springer; 2006.
-
- Brennecke P, et al. Accounting for technical noise in single-cell RNA-seq experiments. Nat. Methods. 2013;10:1093–1095. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

