Optimizing water permeability through the hourglass shape of aquaporins
- PMID: 24067650
- PMCID: PMC3799357
- DOI: 10.1073/pnas.1306447110
Optimizing water permeability through the hourglass shape of aquaporins
Abstract
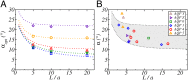
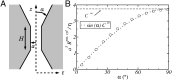
The ubiquitous aquaporin channels are able to conduct water across cell membranes, combining the seemingly antagonist functions of a very high selectivity with a remarkable permeability. Whereas molecular details are obvious keys to perform these tasks, the overall efficiency of transport in such nanopores is also strongly limited by viscous dissipation arising at the connection between the nanoconstriction and the nearby bulk reservoirs. In this contribution, we focus on these so-called entrance effects and specifically examine whether the characteristic hourglass shape of aquaporins may arise from a geometrical optimum for such hydrodynamic dissipation. Using a combination of finite-element calculations and analytical modeling, we show that conical entrances with suitable opening angle can indeed provide a large increase of the overall channel permeability. Moreover, the optimal opening angles that maximize the permeability are found to compare well with the angles measured in a large variety of aquaporins. This suggests that the hourglass shape of aquaporins could be the result of a natural selection process toward optimal hydrodynamic transport. Finally, in a biomimetic perspective, these results provide guidelines to design artificial nanopores with optimal performances.
Keywords: biochannels; hydrodynamic permeability; nanofluidics.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
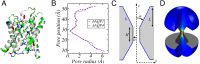
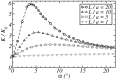
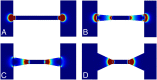
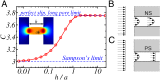
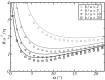
 (see text) as a function of the pore length h for a perfectly slipping cylindrical channel, obtained with FE calculations (points). The red line is a guide for the eyes. (Inset) Velocity field in the considered channel. Color represents the amplitude of the fluid velocity, from blue (slow flow) to red (fast flow). (B and C) Schematic profiles of axial velocity in a channel with no slip (NS) and perfect-slip (PS) BC. From left to right: outside far field, entry profile and inside far field.
(see text) as a function of the pore length h for a perfectly slipping cylindrical channel, obtained with FE calculations (points). The red line is a guide for the eyes. (Inset) Velocity field in the considered channel. Color represents the amplitude of the fluid velocity, from blue (slow flow) to red (fast flow). (B and C) Schematic profiles of axial velocity in a channel with no slip (NS) and perfect-slip (PS) BC. From left to right: outside far field, entry profile and inside far field.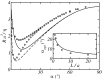
Similar articles
-
[Optimal permeability of aquaporins: a question of shape?].Med Sci (Paris). 2015 Feb;31(2):174-9. doi: 10.1051/medsci/20153102014. Epub 2015 Mar 4. Med Sci (Paris). 2015. PMID: 25744264 Review. French.
-
Molecular Dynamics Simulation of the Effect of Angle Variation on Water Permeability through Hourglass-Shaped Nanopores.Materials (Basel). 2015 Oct 29;8(11):7257-7268. doi: 10.3390/ma8115380. Materials (Basel). 2015. PMID: 28793636 Free PMC article.
-
Large permeabilities of hourglass nanopores: from hydrodynamics to single file transport.J Chem Phys. 2014 Nov 14;141(18):18C526. doi: 10.1063/1.4897253. J Chem Phys. 2014. PMID: 25399191
-
The dynamics and energetics of water permeation and proton exclusion in aquaporins.Curr Opin Struct Biol. 2005 Apr;15(2):176-83. doi: 10.1016/j.sbi.2005.02.003. Curr Opin Struct Biol. 2005. PMID: 15837176 Review.
-
Exploring fast water permeation through aquaporin-mimicking membranes.Phys Chem Chem Phys. 2020 Jan 21;22(3):1333-1348. doi: 10.1039/c9cp05496k. Epub 2019 Dec 19. Phys Chem Chem Phys. 2020. PMID: 31854415
Cited by
-
Water desalination with a single-layer MoS2 nanopore.Nat Commun. 2015 Oct 14;6:8616. doi: 10.1038/ncomms9616. Nat Commun. 2015. PMID: 26465062 Free PMC article.
-
Water permeation through the internal water pathway in activated GPCR rhodopsin.PLoS One. 2017 May 11;12(5):e0176876. doi: 10.1371/journal.pone.0176876. eCollection 2017. PLoS One. 2017. PMID: 28493967 Free PMC article.
-
Experimental and Theoretical Analysis of Metal Complex Diffusion through Cell Monolayer.Entropy (Basel). 2021 Mar 17;23(3):360. doi: 10.3390/e23030360. Entropy (Basel). 2021. PMID: 33802897 Free PMC article.
-
Single-layer membranes for organic solvent nanofiltration: a molecular dynamics simulation and comparative experimental study.RSC Adv. 2022 Mar 2;12(12):7189-7198. doi: 10.1039/d1ra09061e. eCollection 2022 Mar 1. RSC Adv. 2022. PMID: 35424694 Free PMC article.
-
Determination of the Membrane Transport Properties of Jurkat Cells with a Microfluidic Device.Micromachines (Basel). 2019 Nov 29;10(12):832. doi: 10.3390/mi10120832. Micromachines (Basel). 2019. PMID: 31795446 Free PMC article.
References
-
- Borgnia M, Nielsen S, Engel A, Agre P. Cellular and molecular biology of the aquaporin water channels. Annu Rev Biochem. 1999;68:425–458. - PubMed
-
- Agre P. Aquaporin water channels (Nobel Lecture) Angew Chem Int Ed Engl. 2004;43(33):4278–4290. - PubMed
-
- Murata K, et al. Structural determinants of water permeation through aquaporin-1. Nature. 2000;407(6804):599–605. - PubMed
-
- Sui HX, Han BG, Lee JK, Walian P, Jap BK. Structural basis of water-specific transport through the AQP1 water channel. Nature. 2001;414(6866):872–878. - PubMed
-
- Rasaiah JC, Garde S, Hummer G. Water in nonpolar confinement: From nanotubes to proteins and beyond. Annu Rev Phys Chem. 2008;59:713–740. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

