Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Jul 31:13:101.
doi: 10.1186/1471-2288-13-101.

A counterfactual approach to bias and effect modification in terms of response types

Etsuji Suzuki  1 , Toshiharu Mitsuhashi, Toshihide Tsuda, Eiji Yamamoto
Affiliations

A counterfactual approach to bias and effect modification in terms of response types

Etsuji Suzuki et al. BMC Med Res Methodol. .

Abstract

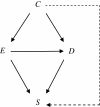
Background: The counterfactual approach provides a clear and coherent framework to think about a variety of important concepts related to causation. Meanwhile, directed acyclic graphs have been used as causal diagrams in epidemiologic research to visually summarize hypothetical relations among variables of interest, providing a clear understanding of underlying causal structures of bias and effect modification. In this study, the authors aim to further clarify the concepts of bias (confounding bias and selection bias) and effect modification in the counterfactual framework.

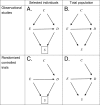
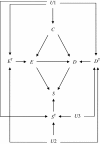
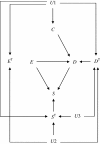
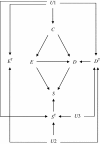
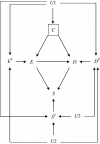
Methods: The authors show how theoretical data frequencies can be described by using unobservable response types both in observational studies and in randomized controlled trials. By using the descriptions of data frequencies, the authors show epidemiologic measures in terms of response types, demonstrating significant distinctions between association measures and effect measures. These descriptions also demonstrate sufficient conditions to estimate effect measures in observational studies. To illustrate the ideas, the authors show how directed acyclic graphs can be extended by integrating response types and observed variables.

Results: This study shows a hitherto unrecognized sufficient condition to estimate effect measures in observational studies by adjusting for confounding bias. The present findings would provide a further understanding of the assumption of conditional exchangeability, clarifying the link between the assumptions for making causal inferences in observational studies and the counterfactual approach. The extension of directed acyclic graphs using response types maintains the integrity of the original directed acyclic graphs, which allows one to understand the underlying causal structure discussed in this study.

Conclusions: The present findings highlight that analytic adjustment for confounders in observational studies has consequences quite different from those of physical control in randomized controlled trials. In particular, the present findings would be of great use when demonstrating the inherent distinctions between observational studies and randomized controlled trials.

PubMed Disclaimer

Figures

Figure 1
Figure 1
A causal diagram depicting a hypothetical example.E, D, C, and S denote exposure, disease, confounder, and selection variable, respectively. C may act as a direct effect modifier simultaneously. In this paper, S is assumed not to be influenced directly by C (i.e., the dashed arrow is absent). The present discussion, however, can be readily extended to the situations in which one assumes that the dashed arrow is present.
Figure 2
Figure 2
Four causal diagrams depicting hypothetical situations.E, D, C, and S denote exposure, disease, confounder, and selection variable, respectively. C may act as a direct effect modifier simultaneously. The square around S in Figure 2A and C indicates that the analysis is restricted to those who do not drop out (i.e., S = 1). By contrast, 2 diagrams in Figure 2B and D show the situations in which information about total population is available to researchers. See text for details.
Figure 3
Figure 3
Frequencies of individuals with 1,024 possible EDS response types in observational studies. We consider 4 binary variables as follows: exposure E, outcome D, confounder C, and selection variable S (see Figure 1). As shown in Tables 1, 2 and 3, we consider 4 response types for E, 16 response types for D, and 16 response types for S. We let EiDjSk denote the EDS response type of [ET = i, DT = j, ST = k], and let PEiDjSk denote a prevalence of the individuals of EiDjSk response type in the total population. We also let PC|EiDjSk and PC¯|EiDjSk denote probabilities of being exposed and unexposed to C among the individuals of EiDjSk response type, respectively. Further, N denotes the number of total population. Those who are classified into inner dashed rectangles represent individuals selected for analyses (i.e., S = 1) while those who are not classified into the rectangles represent non-selected individuals (i.e., S = 0). See text for details.
Figure 4
Figure 4
Frequencies of individuals with 256 possible DS response types in randomized controlled trials. We consider 4 binary variables as follows: exposure E, outcome D, confounder C, and selection variable S (see Figure 1). As shown in Tables 2 and 3, we consider 16 response types for D and 16 response types for S. We let PE and PE¯ denote the probabilities of E and E¯ in the total population, respectively. For the definition of other notations, see Figure 3. Those who are classified into inner dashed rectangles represent individuals selected for analyses (i.e., S = 1) while those who are not classified into the rectangles represent non-selected individuals (i.e., S = 0). See text for details.
Figure 5
Figure 5
An extended causal diagram depicting a hypothetical example.
Figure 6
Figure 6
An extended causal diagram depicting a hypothetical situation under marginal randomization.
Figure 7
Figure 7
An extended causal diagram depicting a hypothetical situation under stratified randomization.
Figure 8
Figure 8
An extended causal diagram depicting a hypothetical situation in observational studies.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Little RJ, Rubin DB. Causal effects in clinical and epidemiological studies via potential outcomes: concepts and analytical approaches. Annu Rev Public Health. 2000;21:121–145. doi: 10.1146/annurev.publhealth.21.1.121. - DOI - PubMed
    1. Pearl J. Causality: Models, Reasoning, and Inference. 2. New York, NY: Cambridge University Press; 2009.
    1. Greenland S, Robins JM. Identifiability, exchangeability, and epidemiological confounding. Int J Epidemiol. 1986;15:413–419. doi: 10.1093/ije/15.3.413. - DOI - PubMed
    1. Greenland S, Robins JM, Pearl J. Confounding and collapsibility in causal inference. Stat Sci. 1999;14:29–46. doi: 10.1214/ss/1009211805. - DOI
    1. Kaufman JS, Poole C. Looking back on "causal thinking in the health sciences". Annu Rev Public Health. 2000;21:101–119. doi: 10.1146/annurev.publhealth.21.1.101. - DOI - PubMed

LinkOut - more resources