Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Jun;41(11):5555-68.
doi: 10.1093/nar/gkt250. Epub 2013 Apr 16.

TherMos: Estimating protein-DNA binding energies from in vivo binding profiles

Wenjie Sun  1 , Xiaoming Hu, Michael H K Lim, Calista K L Ng, Siew Hua Choo, Diogo S Castro, Daniela Drechsel, François Guillemot, Prasanna R Kolatkar, Ralf Jauch, Shyam Prabhakar
Affiliations

TherMos: Estimating protein-DNA binding energies from in vivo binding profiles

Wenjie Sun et al. Nucleic Acids Res. 2013 Jun.

Abstract

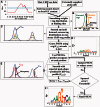
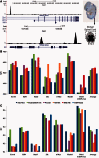
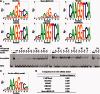
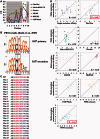
Accurately characterizing transcription factor (TF)-DNA affinity is a central goal of regulatory genomics. Although thermodynamics provides the most natural language for describing the continuous range of TF-DNA affinity, traditional motif discovery algorithms focus instead on classification paradigms that aim to discriminate 'bound' and 'unbound' sequences. Moreover, these algorithms do not directly model the distribution of tags in ChIP-seq data. Here, we present a new algorithm named Thermodynamic Modeling of ChIP-seq (TherMos), which directly estimates a position-specific binding energy matrix (PSEM) from ChIP-seq/exo tag profiles. In cross-validation tests on seven genome-wide TF-DNA binding profiles, one of which we generated via ChIP-seq on a complex developing tissue, TherMos predicted quantitative TF-DNA binding with greater accuracy than five well-known algorithms. We experimentally validated TherMos binding energy models for Klf4 and Esrrb, using a novel protocol to measure PSEMs in vitro. Strikingly, our measurements revealed strong non-additivity at multiple positions within the two PSEMs. Among the algorithms tested, only TherMos was able to model the entire binding energy landscape of Klf4 and Esrrb. Our study reveals new insights into the energetics of TF-DNA binding in vivo and provides an accurate first-principles approach to binding energy inference from ChIP-seq and ChIP-exo data.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
Workflow of the TherMos algorithm. (A) Enrichment of tags in the control library as a function of local GC content. (B) Forward and reverse smoothing weights (tag distribution at binding sites) estimated using an iterative peak refinement procedure. Most tag fragments are <100 bp from the binding site. (C) Construction of ChIP-seq profile (Yobs) from per base pair tag profile. (D) Initial guess of PSEM. (E) Theoretically predicted ChIP-seq profile (Ypred), based on PSEM and inferred average peak shape. (F) PSEM that best fits the Yobs.
Figure 2.
Figure 2.
(A) Mash1 in vivo ChIP-seq profile (E12.5 mouse spinal cord) shows strong peaks at known targets of Mash1. (B, C) Performance of TherMos and other algorithms in 10-fold cross-validation testing on the seven whole-genome TF binding profiles. For each algorithm and each TF, the bar height indicates the average SPE or rank correlation coefficient across the 10 test sets. The summary bars at the end indicate average performance across all seven TFs. (B) SPE is calculated between predicted (motif) and observed (experimental data) ChIP-seq binding profile. Smaller SPE indicates higher accuracy. (C) Rank correlation coefficient is calculated between predicted (motif) and observed (experimental data) ChIP-seq tag counts. Average rank correlation coefficients below zero for some of the algorithms are not shown.
Figure 3.
Figure 3.
In vitro binding energy model for Esrrb and comparison with algorithmic predictions from ChIP-seq. (A) Sequence logos of Esrrb motifs predicted by TherMos, MatrixREDUCE, Weeder, MEME, DREME and ChIPMunk. (B) Results of the EMSA competition assays. (C) The sequence logo of the Esrrb affinity model measured in vitro by EMSA competition assays. (D) Euclidean distance between in vitro motif and the motifs predicted by various algorithms.
Figure 4.
Figure 4.
Position interdependence in Esrrb binding. (A) Euclidean distance at each nucleotide position between in vitro motif and the motifs predicted by various algorithms. (B) Esrra primary and secondary motifs measured using PBM (29). The nucleotides showing positional interdependence are highlighted in the box. (C) The measured affinity by single or multiple mutation EMSA (i.e. the measured log ratio of the Kd of the mutant sequences to Kd of the reference sequence) versus the predicted affinity (i.e. the corresponding predicted log ratio) by single mutation EMSA. Twenty-seven single mutant (diamond) and two multiple mutant (circle) sequences were tested in EMSA competition assays. The consensus (reference) sequence is highlighted in red with the mutated nucleotides highlighted in blue. Error bars for the two multiple-mutant sequences are too small to be visible in this plot.
Figure 5.
Figure 5.
In vitro binding energy model for Klf4 and comparison with the algorithmic predictions from ChIP-seq. (A) Sequence logos of Klf4 motifs predicted by TherMos, MatrixREDUCE, Weeder, MEME, DREME and ChIPMunk. (B) Results of the EMSA competition assays. (C) The sequence logo of the Klf4 affinity model measured in vitro by EMSA competition assays. (D) Euclidean distance between the in vitro motif and the motifs predicted by various algorithms.
Figure 6.
Figure 6.
Position interdependence in Klf4 binding. (A) Euclidean distance at each nucleotide position between the in vitro motif and the motifs predicted by various algorithms from ChIP-seq data. (B) Klf7 primary and secondary motifs measured using PBM (29). The nucleotides showing positional interdependence are highlighted in the box. (C) Twenty-five mutant sequences were tested in multiple mutations EMSA competition assays. The 10-bp consensus sequence is highlighted in red with two flanking nucleotides (in black) at both ends. The mutated nucleotides are highlighted in blue. (D) The multi-mutation measured affinity (i.e. the observed log ratio of the Kd of the 25 mutant sequences to Kd of the Mut 10) versus the corresponding log ratio predicted by single mutation affinity model, TherMos, MatrixREDUCE, Weeder, MEME, DREME, ChIPMunk, PBM primary motif and PBM secondary motif (29). The Pearson correlation coefficient is also shown in the plot.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Stormo GD. Consensus patterns in DNA. Methods Enzymol. 1990;183:211–221. - PubMed
    1. Man TK, Stormo G. Non-independence of Mnt repressor-operator interaction determined by a new quantitative multiple fluorescence relative affinity (QuMFRA) assay. Nucleic Acids Res. 2001;29:2471–2478. - PMC - PubMed
    1. Bulyk ML, Johnson PLF, Church GM. Nucleotides of transcription factor binding sites exert interdependent effects on the binding affinities of transcription factors. Nucleic Acids Res. 2002;30:1255–1261. - PMC - PubMed
    1. Oliphant AR, Brandl CJ, Struhl K. Defining the sequence specificity of DNA-binding proteins by selecting binding sites from random-sequence oligonucleotides: analysis of yeast GCN4 protein. Mol. Cell Biol. 1989;9:2944–2949. - PMC - PubMed
    1. Bailey TL, Elkan C. Proceedings of the Second International Conference on Intelligent Systems for Molecular Biology. Menlo Park, CA: August. AAAI Press; 1994. Fitting a mixture model by expectation maximization to discover motifs in biopolymers; pp. 28–36. - PubMed

Publication types