Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2012 Jul 3;109(27):10849-54.
doi: 10.1073/pnas.1200160109. Epub 2012 Jun 18.

Theory of active transport in filopodia and stereocilia

Pavel I Zhuravlev  1 , Yueheng Lan, Maria S Minakova, Garegin A Papoian
Affiliations

Theory of active transport in filopodia and stereocilia

Pavel I Zhuravlev et al. Proc Natl Acad Sci U S A. .

Abstract

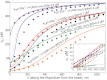
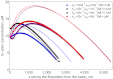
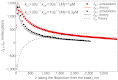
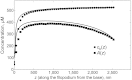
The biological processes in elongated organelles of living cells are often regulated by molecular motor transport. We determined spatial distributions of motors in such organelles, corresponding to a basic scenario when motors only walk along the substrate, bind, unbind, and diffuse. We developed a mean-field model, which quantitatively reproduces elaborate stochastic simulation results as well as provides a physical interpretation of experimentally observed distributions of Myosin IIIa in stereocilia and filopodia. The mean-field model showed that the jamming of the walking motors is conspicuous, and therefore damps the active motor flux. However, when the motor distributions are coupled to the delivery of actin monomers toward the tip, even the concentration bump of G actin that they create before they jam is enough to speed up the diffusion to allow for severalfold longer filopodia. We found that the concentration profile of G actin along the filopodium is rather nontrivial, containing a narrow minimum near the base followed by a broad maximum. For efficient enough actin transport, this nonmonotonous shape is expected to occur under a broad set of conditions. We also find that the stationary motor distribution is universal for the given set of model parameters regardless of the organelle length, which follows from the form of the kinetic equations and the boundary conditions.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Fig. 1.
Fig. 1.
A representation of the filopodial model is shown with kinetics scheme of chemical reactions. A filopodium is a cylindrical tube with a bundle of parallel actin filaments inside enveloped by cell’s membrane. The motors can walk on filaments (with speed v determined by forward and backward stepping rates) or diffuse in the solution (with diffusion constant of 5 μm2/s). They can bind and unbind to the filaments (with rates kon and koff) and, when on filaments, load, and unload G actin (with rates kl and kul). A loaded motor can detach from the filament simultaneously releasing G actin. Thus, there is no G actin bound to motors in the solution, fulfilling the nonsequestrating regime condition.
Fig. 2.
Fig. 2.
Comparison of the mean-field analytical models with the stochastic simulation results. The dashed line is the phantom motors model, the solid line is the FFC model, where limited number of binding sites on the filaments is taken into account. Circles are simulation results for cb, and squares for cf. Inset zooms into low concentration region to show curves for cf.
Fig. 3.
Fig. 3.
Motor concentration profiles inside a filopodium are shown according to stochastic simulations and jammed motors model for various parameter sets (motor affinity to filaments, motor speed, motor concentration). For each set of parameters, the simulations points continue up to the filopodial length from the corresponding simulation. Theoretical curves were computed for all lengths. Inset zooms into low concentration region to show curves for cf. Circles correspond to simulations, solid lines to the numerical solution of the mean-field theory, and dashed lines to analytical solution of the mean-field theory using the approximation of weakly violated detailed balance.
Fig. 4.
Fig. 4.
G-actin concentration profiles for different parameter values are shown. Circles represent the results of stochastic simulations and lines are the solutions of Eq. 6 for a(z). All the profiles end when the concentration drops below atip (Eq. 5), which is about 2.3 μM for our parameter values.
Fig. 5.
Fig. 5.
Active transport fluxes for different parameter values are calculated as JAT(z) = (v[1 - cb(z)/cs] - vr)A(z). Symbols correspond to A(z) and cb(z) taken from the results of stochastic simulations, and lines are plotted by taking cb(z) and A(z) from the solutions of Eqs. 2 and 6. Active transport flux decreases after the traffic jam is formed. The retrograde flow flux Jr of 415 molecules per second determines the flux of G-actin monomers, which need to be delivered to the tip at steady state. Dashed line shows the diffusional forward flux of G actin for kul = 30 s-1, koff = 10 s-1, [M] = 0.3 μM (corresponding to the black curve on Fig. 4). Active flux is still significant even far from the start of the jam, however, starts to vanish near the tip.
Fig. 6.
Fig. 6.
Concentration profiles for actin-on-the-motors A(z) and motors cb(z) are shown for kul = 30 s-1, koff = 10 s-1, [M] = 0.3 μM (corresponding to the black curve on Fig. 4) from analytical solution. The concentration of F-actin binding sites cs = N/Sδ = 558 μM caps cb(z), while A(z) is in turn capped by cb(z). Symbols correspond to A(z) and cb(z) taken from the results of stochastic simulations, and lines are plotted by taking cb(z) and A(z) from the solutions of Eqs. 2 and 6.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Bagnard D, editor. Axon growth and guidance. Adv Exp Med Biol. 2007;621:5–6. - PubMed
    1. Riedel-Kruse IH, Hilfinger A, Howard J, Jülicher F. How molecular motors shape the flagellar beat. HFSP J. 2007;1:192–208. - PMC - PubMed
    1. Sousa AD, Cheney RE. Myosin-X: A molecular motor at the cell’s fingertips. Trends Cell Biol. 2005;15:533–539. - PubMed
    1. Prost J, Barbetta C, Joanny JF. Dynamical control of the shape and size of stereocilia and microvilli. Biophys J. 2007;93:1124–1133. - PMC - PubMed
    1. Salles FT, et al. Myosin IIIa boosts elongation of stereocilia by transporting espin 1 to the plus ends of actin filaments. Nat Cell Biol. 2009;11:443–450. - PMC - PubMed

Publication types

LinkOut - more resources