Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2012;8(3):e1002392.
doi: 10.1371/journal.pcbi.1002392. Epub 2012 Mar 15.

Cell shape dynamics: from waves to migration

Meghan K Driscoll  1 , Colin McCann, Rael Kopace, Tess Homan, John T Fourkas, Carole Parent, Wolfgang Losert
Affiliations

Cell shape dynamics: from waves to migration

Meghan K Driscoll et al. PLoS Comput Biol. 2012.

Abstract

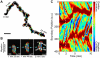
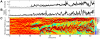
We observe and quantify wave-like characteristics of amoeboid migration. Using the amoeba Dictyostelium discoideum, a model system for the study of chemotaxis, we demonstrate that cell shape changes in a wave-like manner. Cells have regions of high boundary curvature that propagate from the leading edge toward the back, usually along alternating sides of the cell. Curvature waves are easily seen in cells that do not adhere to a surface, such as cells that are electrostatically repelled from surfaces or cells that extend over the edge of micro-fabricated cliffs. Without surface contact, curvature waves travel from the leading edge to the back of a cell at -35 µm/min. Non-adherent myosin II null cells do not exhibit these curvature waves. At the leading edge of adherent cells, curvature waves are associated with protrusive activity. Like regions of high curvature, protrusive activity travels along the boundary in a wave-like manner. Upon contact with a surface, the protrusions stop moving relative to the surface, and the boundary shape thus reflects the history of protrusive motion. The wave-like character of protrusions provides a plausible mechanism for the zig-zagging of pseudopods and for the ability of cells both to swim in viscous fluids and to navigate complex three dimensional topography.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Figure 1
Figure 1. The boundary curvature of a self-aggregating wild-type Dictyostelium cell.
(A) The overlapped light gray boundaries show the shape every 4 seconds, while the alternating dark gray and colored boundaries show the shape every 2 minutes. Colored boundaries represent curvature. (Scale bar, 20 µm.) (B) The boundary curvature overlaid on the original fluorescence images (video S1). Two curvature peaks, indicated by teal arrows, remain at the same location as the cell migrates through them. Numbers label the indices of every 100th boundary point (video S2). (Scale bar, 5 µm.) (C) The spatial and temporal evolution of boundary curvature can be visualized in a kymograph. Peaks in boundary curvature propagate from the cell front (initially near boundary point 150) to the cell back (initially near boundary point 350).
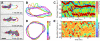
Figure 2
Figure 2. The interaction of boundary curvature waves with the substrate.
(A) An IRM image sequence overlaid with the boundary of the surface contact region, shown in purple, and the boundary of the entire cell, shown colored by curvature (video S4). At the sides of cells, peaks in cell boundary curvature are located near peaks in surface contact region boundary curvature. Both of these curvature peaks are stationary with respect to the substrate. (Scale bar, 5 µm.) (B) The overlaid shapes of an aca − (non cAMP releasing) cell that is electrostatically repulsed from the substrate, and so is not adhered to the surface. The curvature peak that travels from the cell front to the cell back is moving with respect to the substrate. The centroid positions were aligned to account for drift. (4 sec. apart.) (C) The boundary curvature kymograph of this non-adherent cell (video S5). (D) The overlaid shapes of a non-adherent, myosin II null cell. While the cell extends regions of transient protrusive activity, it has no apparent curvature waves. (4 sec. apart.) (E) The boundary curvature kymograph of this non-adherent myosin II null cell.
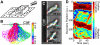
Figure 3
Figure 3. Boundary curvature waves on cells that are extended over the edge of a cliff.
(A) A schematic of the 3-D surface on which cells are guided over a cliff edge. The surface closest to a cAMP-releasing needle is the cliff edge. (B) The overlaid boundaries show a cell extended over the edge of a cliff and wiggling rapidly (boundaries are 1.6 seconds apart). (C) An image sequence of a propagating curvature wave. (video S5). (Scale bar, 5 µm.) (D) The corresponding curvature kymograph, showing multiple curvature waves.
Figure 4
Figure 4. Polarity symmetry breaking of an aca − (non cAMP releasing) cell.
(A) During polarization, non-circularity, the normalized ratio of perimeter to the perimeter of a circle with the same area, increases in an oscillatory fashion. (B) The speed of the cell centroid. (C) Boundary curvature, which prior to polarization is mostly static, begins exhibiting organized curvature waves (video S7).
Figure 5
Figure 5. The initialization of curvature waves is associated with protrusive motion.
(A) The boundary curvature kymograph of the cell shown in figure 2a . Curvature waves, shown as dashed black lines, are drawn on. (B) One measure of local boundary speed is the magnitude of the motion mapping. Here, the cell shape at 6 minutes is shown as the black boundary, while the shape 12 seconds later is the gray boundary. The motion mapping vectors, shown here colored by magnitude (colormap as in c), connect the boundary points in the earlier frame to boundary points in the later frame. Only every eighth mapping vector is shown. (C) The local motion kymograph with the overlaid position of the curvature waves, which appear as dashed black lines. Protrusive events usually coincide with the initialization of curvature waves.
Figure 6
Figure 6. Boundary motion can be analyzed as a series of discrete protrusive and retractive events or as continuous movement.
(A) In this plot of the evolution of local boundary motion, protrusive motion appears red, while retractive motion appears blue (video S9). (B) Extracted individual protrusions are shown as black dots, while extracted retractions are shown as white dots. (C) The averaged location of protrusive and retractive motion, which is defined in each frame where boundary motion is above a noise threshold, are shown here. This cell is also shown in figure 1 . (D) The mean squared displacement of the mean protrusive location is ballistic on short time-scales. The black lines, from left to right, have slopes of 2, 1 and 0 micrometers/min.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Wagle MA, Tranquillo RT. A self-consistent cell flux expression for simultaneous chemotaxis and contact guidance in tissues. J Math Biol. 2000;41:315–330. - PubMed
    1. Yang X, Dormann D, Munsterberg AE, Weijer CJ. Cell movement patterns during gastrulation in the chick are controlled by positive and negative chemotaxis mediated by FGF4 and FGF8. Dev Cell. 2002;3:425–437. - PubMed
    1. Capogrosso Sansone B, Scalerandi M, Condat CA. Emergence of taxis and synergy in angiogenesis. Phys Rev Lett. 2001;87:128102. - PubMed
    1. Kassis J, Lauffenburger DA, Turner T, Wells A. Tumor invasion as dysregulated cell motility. Semin Cancer Biol. 2001;11:105–117. - PubMed
    1. Bagorda A, Parent CA. Eukaryotic chemotaxis at a glance. J Cell Sci. 2008;121:2621–2624. - PMC - PubMed

Publication types