Mechanisms for Phase Shifting in Cortical Networks and their Role in Communication through Coherence
- PMID: 21103013
- PMCID: PMC2987601
- DOI: 10.3389/fnhum.2010.00196
Mechanisms for Phase Shifting in Cortical Networks and their Role in Communication through Coherence
Abstract
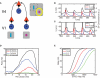
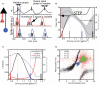
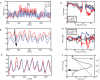
In the primate visual cortex, the phase of spikes relative to oscillations in the local field potential (LFP) in the gamma frequency range (30-80 Hz) can be shifted by stimulus features such as orientation and thus the phase may carry information about stimulus identity. According to the principle of communication through coherence (CTC), the relative LFP phase between the LFPs in the sending and receiving circuits affects the effectiveness of the transmission. CTC predicts that phase shifting can be used for stimulus selection. We review and investigate phase shifting in models of periodically driven single neurons and compare it with phase shifting in models of cortical networks. In a single neuron, as the driving current is increased, the spike phase varies systematically while the firing rate remains constant. In a network model of reciprocally connected excitatory (E) and inhibitory (I) cells phase shifting occurs in response to both injection of constant depolarizing currents and to brief pulses to I cells. These simple models provide an account for phase-shifting observed experimentally and suggest a mechanism for implementing CTC. We discuss how this hypothesis can be tested experimentally using optogenetic techniques.
Keywords: attention; gamma oscillations; phase locking; phase shifting; synchrony.
Figures

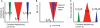
Similar articles
-
Inhibitory synchrony as a mechanism for attentional gain modulation.J Physiol Paris. 2004 Jul-Nov;98(4-6):296-314. doi: 10.1016/j.jphysparis.2005.09.002. Epub 2005 Nov 7. J Physiol Paris. 2004. PMID: 16274973 Free PMC article.
-
Cortical dynamics during naturalistic sensory stimulations: experiments and models.J Physiol Paris. 2011 Jan-Jun;105(1-3):2-15. doi: 10.1016/j.jphysparis.2011.07.014. Epub 2011 Aug 31. J Physiol Paris. 2011. PMID: 21907800
-
Role of frequency mismatch in neuronal communication through coherence.J Comput Neurosci. 2014 Oct;37(2):193-208. doi: 10.1007/s10827-014-0495-7. Epub 2014 Feb 12. J Comput Neurosci. 2014. PMID: 24519733
-
Spike-Gamma Phase Relationship in the Visual Cortex.Annu Rev Vis Sci. 2022 Sep 15;8:361-381. doi: 10.1146/annurev-vision-100419-104530. Epub 2022 Jun 6. Annu Rev Vis Sci. 2022. PMID: 35667158 Review.
-
From mechanisms to functions: The role of theta and gamma coherence in the intrahippocampal circuits.Hippocampus. 2022 May;32(5):342-358. doi: 10.1002/hipo.23410. Epub 2022 Feb 22. Hippocampus. 2022. PMID: 35192228 Review.
Cited by
-
Analytical insights on theta-gamma coupled neural oscillators.J Math Neurosci. 2013 Aug 14;3(1):16. doi: 10.1186/2190-8567-3-16. J Math Neurosci. 2013. PMID: 23945442 Free PMC article.
-
Dynamic circuit motifs underlying rhythmic gain control, gating and integration.Nat Neurosci. 2014 Aug;17(8):1031-9. doi: 10.1038/nn.3764. Epub 2014 Jul 28. Nat Neurosci. 2014. PMID: 25065440 Review.
-
Controlling the oscillation phase through precisely timed closed-loop optogenetic stimulation: a computational study.Front Neural Circuits. 2013 Apr 17;7:49. doi: 10.3389/fncir.2013.00049. eCollection 2013. Front Neural Circuits. 2013. PMID: 23616748 Free PMC article.
-
Switching neuronal inputs by differential modulations of gamma-band phase-coherence.J Neurosci. 2012 Nov 14;32(46):16172-80. doi: 10.1523/JNEUROSCI.0890-12.2012. J Neurosci. 2012. PMID: 23152601 Free PMC article.
-
Phase-locking patterns underlying effective communication in exact firing rate models of neural networks.PLoS Comput Biol. 2022 May 18;18(5):e1009342. doi: 10.1371/journal.pcbi.1009342. eCollection 2022 May. PLoS Comput Biol. 2022. PMID: 35584147 Free PMC article.
References
-
- Ardid S., Wang X. J., Gomez-Cabrero D., Compte A. (2010). Reconciling coherent oscillation with modulation of irregular spiking activity in selective attention: gamma-range synchronization between sensory and executive cortical areas. J. Neurosci. 30, 2856–287010.1523/JNEUROSCI.4222-09.2010 - DOI - PMC - PubMed
-
- Bernander O., Koch C., Usher M. (1994). The effect of synchronized inputs at the single neuron level. Neural Comput. 6, 622–64110.1162/neco.1994.6.4.622 - DOI
LinkOut - more resources
Full Text Sources

