Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2011 Jun 7;278(1712):1661-9.
doi: 10.1098/rspb.2010.2020. Epub 2010 Nov 10.

Epidemic malaria and warmer temperatures in recent decades in an East African highland

David Alonso  1 , Menno J Bouma, Mercedes Pascual
Affiliations

Epidemic malaria and warmer temperatures in recent decades in an East African highland

David Alonso et al. Proc Biol Sci. .

Abstract

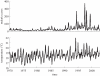
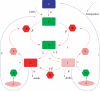
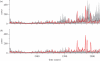
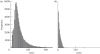
Climate change impacts on malaria are typically assessed with scenarios for the long-term future. Here we focus instead on the recent past (1970-2003) to address whether warmer temperatures have already increased the incidence of malaria in a highland region of East Africa. Our analyses rely on a new coupled mosquito-human model of malaria, which we use to compare projected disease levels with and without the observed temperature trend. Predicted malaria cases exhibit a highly nonlinear response to warming, with a significant increase from the 1970s to the 1990s, although typical epidemic sizes are below those observed. These findings suggest that climate change has already played an important role in the exacerbation of malaria in this region. As the observed changes in malaria are even larger than those predicted by our model, other factors previously suggested to explain all of the increase in malaria may be enhancing the impact of climate change.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
Monthly time series for (a) malaria cases and (b) mean temperatures. The malaria data consist of confirmed cases for inpatients from the admission records for 1966–2002 at the hospital serving a tea plantation composed of several estates (Brooke Bond Farms, now Unilever Tea Kenya Ltd; latitude 0.3° S, longitude 35.37° E, elevation 1780–2225 m) [15]. The temperature data were obtained by dovetailing the records from two meteorological stations within the tea estates, together with adjustments for altitude based on mean temperature data from a number of stations in Kenya spanning a broader altitude range (see §2 and electronic supplementary material, figure S1 and §5 for details). The data from the Tea Research Foundation (TRF) meteorological station were used up to 1992, and from December 1997 to March 1998 when the second record was missing; the data from the official meteorological station were used from 1992 onwards by adjusting these to the altitude of the TRF time series. The graph shows the temperature time series adjusted for 1780 m.
Figure 2.
Figure 2.
Coupled mosquito–human model of malaria dynamics. The population is subdivided into a number of classes. In particular, two types of infected individual are considered: those who present symptoms and therefore receive some sort of clinical treatment (C), and those who acquire asymptomatic infection (I) but are nevertheless infectious and can transmit the parasite to the vector. A recovered class (R) consists of individuals who have cleared parasitaemia, or have too low a level of parasitaemia to effectively infect the vector. The replenishment of susceptibles through immigration or births (B) and individual losses owing to mortality—or more generally, population turnover (δ)—are considered to balance each other so that the total population N remains constant. A constant maximum size of the worker population and their dependants in the tea estates supports this assumption [15]. The coupling to the mosquito component of the model occurs through the ‘force of infection’ (β), the per capita rate at which susceptible individuals become infected. This rate contains two terms to allow for two different sources of infection, for local and external transmission, respectively (electronic supplementary material). The local force of infection depends on the number of infected mosquitoes W, and the mosquito population is subdivided into larvae (L), and adults, with uninfected adults (X) becoming exposed (V) when they bite an infectious human (electronic supplementary material). Only a fraction of infections in humans (ξ) fully develops severe malaria symptoms and then receives clinical treatment (C). Asymptomatic but infectious individuals (I) can present a relapse of severe malaria symptoms if they are bitten again, but the per capita transmission rate (β) of this process is decreased by a factor η. The clearance or recovery rate for treated infected and sick (C) and non-treated infected individuals (I) are ρ and r, respectively. Recovered individuals in R lose immunity at rate σ and return to S with a relaxation time that depends on mosquito exposure (see electronic supplementary material for details).
Figure 3.
Figure 3.
Numerical simulations of the model (a) with and (b) without the trend in temperature. The numerical simulations generate a distribution of cases for each month reflecting the uncertainty in parameter values of the model (electronic supplementary material). There are three sources of uncertainty in these simulations. First, our parameter search produces a family of solutions. We use this whole family of parameter sets to simulate the model repeatedly. Second, each simulation without the trend considers a different random sample of temperatures in the 1970s. Third, the model includes an error model to account for uncontrolled, unavoidable variability from processes not explicitly modelled in our deterministic approach. Thus, the resulting simulations give us a distribution of cases (as well as infected numbers) for each month. We plot here the median number of cases (50% percentile, dark grey line), together with the range from the 5 to 95% percentiles (light grey shading) of the distribution of predicted cases for each month. Comparison of (a) with (b) shows the effect of warmer temperatures on the dynamics of the malaria model. The observed cases are plotted in red.
Figure 4.
Figure 4.
Histograms of predicted cases at the seasonal peaks for the model (a) with and (b) without the trend in temperatures.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. MacDonald G. 1957. The epidemiology and control of malaria. Oxford, UK: Oxford University Press
    1. Metselaar D., van Theil P. M. 1959. Classification of malaria. Trop. Geogr. Med. 11, 157–161
    1. Detinova T. 1962. Age-grouping methods in Diptera of medical importance, vol. 47 World Health Organization Monograph Series Geneva, Switzerland: World Health Organization - PubMed
    1. Lindsay S. W., Birley M. H. 1996. Climate change and malaria transmission. Ann. Trop. Med. Parasitol. 90, 573–588 - PubMed
    1. Rogers D. J., Randolph S. E. 2000. The global spread of malaria in a future, warmer world. Science 289, 1763–176610.1126/science.289.5478.391b (doi:10.1126/science.289.5478.391b) - DOI - DOI - PubMed

Publication types