Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2009 Oct;38(8):1079-99.
doi: 10.1007/s00249-009-0514-1. Epub 2009 Jul 31.

On the analysis of sedimentation velocity in the study of protein complexes

Patrick H Brown  1 , Andrea Balbo, Peter Schuck
Affiliations

On the analysis of sedimentation velocity in the study of protein complexes

Patrick H Brown et al. Eur Biophys J. 2009 Oct.

Abstract

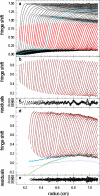
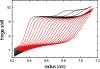
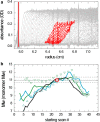
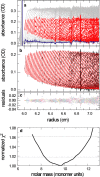
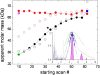
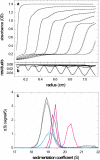
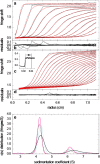
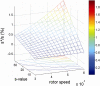
Sedimentation velocity analytical ultracentrifugation has experienced a significant transformation, precipitated by the possibility of efficiently fitting Lamm equation solutions to the experimental data. The precision of this approach depends on the ability to account for the imperfections of the experiment, both regarding the sample and the instrument. In the present work, we explore in more detail the relationship between the sedimentation process, its detection, and the model used in the mathematical data analysis. We focus on configurations that produce steep and fast-moving sedimentation boundaries, such as frequently encountered when studying large multi-protein complexes. First, as a computational tool facilitating the analysis of heterogeneous samples, we introduce the strategy of partial boundary modeling. It can simplify the modeling by restricting the direct boundary analysis to species with sedimentation coefficients in a predefined range. Next, we examine factors related to the experimental detection, including the magnitude of optical aberrations generated by out-of-focus solution columns at high protein concentrations, the relationship between the experimentally recorded signature of the meniscus and the meniscus parameter in the data analysis, and the consequences of the limited radial and temporal resolution of the absorbance optical scanning system. Surprisingly, we find that large errors can be caused by the finite scanning speed of the commercial absorbance optics, exceeding the statistical errors in the measured sedimentation coefficients by more than an order of magnitude. We describe how these effects can be computationally accounted for in SEDFIT and SEDPHAT.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
a Sedimentation profiles of thyroglobulin sedimenting at 50,000 rpm. For clarity, TI and RI noise contributions initially estimated from a standard c(s) analysis of the whole profiles were subtracted. Highlighted in red are the partial boundary segments defined with the apparent s-values of 17 and 20 S. In order to demonstrate the shape of the boundary and the relative location of the slow- and fast-moving boundaries at a single point in time, one profile is highlighted in blue. b The PBM region of the raw data (black lines) being fit with the partial boundary model (dashed red lines) using a single-species model. The residuals are shown in c. d A larger analysis window in PBM (15–21 S) is used for PBM accounting directly for TI and RI noise. The data are shown in black, the fit as red dashed line. The first several scans are eliminated due to insufficient overlap. The best-fit TI noise profile is shown as a green line, which can be compared to the TI noise estimate from the whole boundary c(s) model in gray. After eliminating the RI noise from scan alignment with a preliminary whole boundary analysis, the TI noise estimate derived from PBM is shown as a blue solid line. e Residuals from d
Fig. 2
Fig. 2
Schematic of the selection of PBM limits for heterogeneous systems that exhibit both small and large species. To illustrate the recommended strategy, the black solid lines are simulated sedimentation data for three species of 0.3, 6, and 20 S. The red portion highlights the partial boundary for apparent s-values ranging from 1 to 8 S, which includes a large portion of the boundary spread from the small species, such that their influence on the main boundary can be accurately assessed, but no signal from the large species that can be excluded from consideration in the model
Fig. 3a, b
Fig. 3a, b
Analysis of the absorbance data from the sedimentation of TRAP used as a model system by Philo (2006). a Overlay of all experimental absorbance scans (gray) and the selection subjected to the data analysis by Philo (red) (Philo 2006), consisting of data with apparent s*-values between 4.39 and 6.28 S from scans #23 to #34. The meniscus value assumed in Philo’s analysis is indicated as bold vertical red line. b Dependence of the result from Philo’s approach on the particular set of scans included in the analysis. Shown are the molar mass estimates for sequences of scans starting with the number indicated in the abscissa, for total scan numbers of 8 scans (bold black line), 12 scans (green line), or 16 scans (blue line). Also indicated are the results obtained for 12 scans with a shift of the assumed meniscus position by –0.01 cm and a slightly narrower analysis interval including s*-values from 4.65 to 6.03 S (down triangles), and for 12 scans with a shift of the assumed meniscus position by +0.01 cm and a slightly wider analysis interval including s*-values from 4.03 to 6.91 S (up triangles). The thin black horizontal line indicates the expected value from the literature (11.0), and the red circle indicates the conditions for which the results were reported by Philo. The dashed black lines are the limits of the 95% confidence interval reported by Philo
Fig. 4a–d
Fig. 4a–d
Analysis of the same absorbance data as in Fig. 3, but considering the information from all scans. a Overlay of all experimental absorbance scans (gray) and segments with apparent s*-values between 4.39 and 6.28 S (equivalent to those in Fig. 3). The PBM analysis permits calculating the best-fit meniscus position, as indicated by the black vertical line. The best-fit estimate of the TI noise profile is indicated by the blue line. b Enhanced view of the data (black lines) and fit (red lines) of the PBM analysis, for clarity with the TI noise estimates subtracted. c Residuals of the fit, using different colors in consecutive scans. d Normalized χ2 as a function of molar mass in monomer units, calculated with the error surface projection method of fixing the molar mass value to the values indicated while floating all other parameters. The horizontal dashed lines are the critical χ2-values for one and two standard deviation confidence levels
Fig. 5
Fig. 5
Dependence of the best-fit apparent molar mass value, as determined from a single-species Lamm equation model in PBM of the raw data (red), on the choice of scan subsets. For comparison, the results are shown of the analogous analysis when using the improved g(s*) fit with transformed Lamm equation solutions (black). All scan subsets use scan #69 as the last scan, with an interval starting with the scan number indicated in the abscissa (i.e., using 60 scans for the first data point, and only 8 scans for the last data point). The sedimentation coefficient range used in the analysis by both approaches was either fixed to the interval from 3.568 S to 5.593 S (filled circles), or adjusted for each scan selection such as to represent the width of the normalized g(s*) distribution at half-height (open circles). Shown at the coordinate 51.2 kDa/scan #32 (black star) is the best-fit apparent mass resulting from the single-species fit of the g(s*) distribution for the subset of scans from #32 to #43 suggested by the dcdt+ wizard. The fixed s-value interval from 3.5681 to 5.5933 S corresponds to the half-height of the g(s*) peak for these conditions. The inset shows the g(s*) curve for the wizard-selected conditions (dashed gray), with all scans included (green), and with the smallest subset (blue), all normalized to the same peak height. Solid lines indicate their adjusted s-range. A PBM c(s) distribution derived from the widest scan set with the adjusted s-range is shown as magenta area plot. It leads to a frictional ratio that yields a peak M-value as indicated by the magenta circle in the main plot
Fig. 6a–c
Fig. 6a–c
The time-delay of scanning in the absorbance optical system. a Experimental absorbance profiles of thyroglobulin sedimenting at 50,000 rpm (solid lines) recorded with standard 0.003-cm radial increment. Data were fit with a superposition of Lamm equation solution accounting for the finite scanning velocity of 2.5 cm/min, which allowed to predict the theoretical absorbance profiles that would have been recorded with instantaneous detection (dashed line). b Difference between experimental and theoretical curves. c Best-fit uncorrected c(s) traces of SV data from three cells with absorbance optical data acquisition in radial increments of 0.003 cm and single (magenta solid line), double (magenta dotted line), and quadruple (magenta dashed line) acquisition at each radial point. The c(s) traces from the interference optical data acquired simultaneously from the same cells are shown in black. After corrections were applied to the c(s) distribution for the predicted scanner velocity, the blue curves were obtained
Fig. 7a–e
Fig. 7a–e
Interference optical data from a sedimentation experiment with convection. BSA was sedimented at 50,000 rpm at 20°C after preincubation of the rotor at 25°C. a Experimental fringe profiles (black lines) and best-fit c(s) model (red lines) with the meniscus fixed to the optical meniscus artifact. Due to the presence of convection, a poor fit is obtained with RMSD of 0.0195 fringes. b Residuals of the fit. c Constraining the analysis to the experimental scans recorded after 3,800 s (black lines) leads to an improved fit quality (red lines) with RMSD of 0.0061 fringes. The inset shows the meniscus region with the best-fit meniscus position indicated as a red vertical line. If the meniscus is fixed to the optical artifact (blue line in the inset), a significantly worse fit with RMSD of 0.0079 fringes is obtained (data not shown). d Residuals of the fit. ec(s) distributions from different analyses of the data: the complete data with graphically constrained meniscus as shown in a (solid black line) leading to s1 = 4.31 S, f/f0 = 1.54, and M1 = 77.4 kDa; the late data with floating meniscus as shown in c (solid magenta line) leading to s1 = 4.2 S, f/f0 = 1.47, and M1 = 69.2 kDa; the late data with constrained meniscus (dotted blue line) leading to s1 = 4.31 S, f/f0 = 1.47, and M1 = 71.4 kDa; and the c(s) distribution of a reference experiment without convection (dotted black line) leading to s1 = 4.21 S, f/f0 = 1.47, and M1 = 68.9 kDa
Fig. 8
Fig. 8
Predicted relative error in the apparent sedimentation coefficient as a function of true s-value (in S) and rotor speed (in rpm) when uncorrected for the finite time of scanning. Standard conditions are assumed, with a solution column corresponding to a 400 μl sample and a scanning speed of 2.5 cm/min, approximately that obtained with standard acquisition parameters with a 0.003 cm radial increment and continuous acquisition of a single reading per radial value
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Balbo A, Brown P et al (2007) Step-by-step protocol for sedimentation velocity analytical ultracentrifugation. http://www.analyticalultracentrifugation.com/svprotocols.htm
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1073/pnas.0408399102', 'is_inner': False, 'url': 'https://doi.org/10.1073/pnas.0408399102'}, {'type': 'PMC', 'value': 'PMC538923', 'is_inner': False, 'url': 'https://pmc.ncbi.nlm.nih.gov/articles/PMC538923/'}, {'type': 'PubMed', 'value': '15613487', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/15613487/'}]}
    2. Balbo A, Minor KH et al (2005) Studying multi-protein complexes by multi-signal sedimentation velocity analytical ultracentrifugation. Proc Natl Acad Sci USA 102:81–86 - PMC - PubMed
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1016/S0301-4622(01)00248-4', 'is_inner': False, 'url': 'https://doi.org/10.1016/s0301-4622(01)00248-4'}, {'type': 'PubMed', 'value': '11880173', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/11880173/'}]}
    2. Behlke J, Ristau O (2002) A new approximate whole boundary solution of the Lamm differential equation for the analysis of sedimentation velocity experiments. Biophys Chem 95(1):59–68 - PubMed
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1208/aapsj080368', 'is_inner': False, 'url': 'https://doi.org/10.1208/aapsj080368'}, {'type': 'PMC', 'value': 'PMC2761066', 'is_inner': False, 'url': 'https://pmc.ncbi.nlm.nih.gov/articles/PMC2761066/'}, {'type': 'PubMed', 'value': '17025277', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/17025277/'}]}
    2. Berkowitz SA (2006) Role of analytical ultracentrifugation in assessing the aggregation of protein biopharmaceuticals. AAPS J 8(3):E590–E605 - PMC - PubMed
    1. {'text': '', 'ref_index': 1, 'ids': [{'type': 'DOI', 'value': '10.1529/biophysj.106.081372', 'is_inner': False, 'url': 'https://doi.org/10.1529/biophysj.106.081372'}, {'type': 'PMC', 'value': 'PMC1471869', 'is_inner': False, 'url': 'https://pmc.ncbi.nlm.nih.gov/articles/PMC1471869/'}, {'type': 'PubMed', 'value': '16565040', 'is_inner': True, 'url': 'https://pubmed.ncbi.nlm.nih.gov/16565040/'}]}
    2. Brown PH, Schuck P (2006) Macromolecular size-and-shape distributions by sedimentation velocity analytical ultracentrifugation. Biophys J 90:4651–4661 - PMC - PubMed

Publication types

Substances

LinkOut - more resources