Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2008 Aug 28;59(4):530-45.
doi: 10.1016/j.neuron.2008.07.012.

Making an effort to listen: mechanical amplification in the ear

A J Hudspeth  1
Affiliations
Review

Making an effort to listen: mechanical amplification in the ear

A J Hudspeth. Neuron. .

Abstract

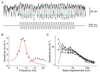
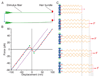
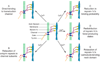
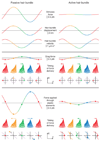
The inner ear's performance is greatly enhanced by an active process defined by four features: amplification, frequency selectivity, compressive nonlinearity, and spontaneous otoacoustic emission. These characteristics emerge naturally if the mechanoelectrical transduction process operates near a dynamical instability, the Hopf bifurcation, whose mathematical properties account for specific aspects of our hearing. The active process of nonmammalian tetrapods depends upon active hair-bundle motility, which emerges from the interaction of negative hair-bundle stiffness and myosin-based adaptation motors. Taken together, these phenomena explain the four characteristics of the ear's active process. In the high-frequency region of the mammalian cochlea, the active process is dominated instead by the phenomenon of electromotility, in which the cell bodies of outer hair cells extend and contract as the protein prestin alters its membrane surface area in response to changes in membrane potential.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Hair cells and their transduction process (A) The sensory epithelium of the chicken's cochea displays a regular, hexagonal array of short hair cells bordered by narrow, microvillus-bearing supporting cells. These short hair cells, which receive no afferent innervation but copious efferent innervation, are thought to contribute to transduction through active hair-bundle motility. (B) A lateral view of hair bundles from the same preparation emphasizes the systematic increase in stereociliary length across each hair bundle. Deflecting the top of any of these bundles to the right would depolarize the associated hair cell; leftward motion would produce a hyperpolarization. (C) A higher-power view of a single hair bundle shows the orderly array of stereocilia, some of which remain connected by tip links (arrowhead). (D) This schematic depiction of a resting hair bundle shows two stereocilia connected by a tip link attached to a transduction channel (left diagram). Deflection of the bundle by a positively directed mechanical stimulus bends the stereociliary pivots, tenses the tip link, and opens the transduction channel, allowing K+ and Ca2+ to enter the cytoplasm and depolarize the hair cell (middle diagram). Ca2+ that enters through the channel then interacts with a molecular motor comprising myosin-1c molecules and causes it to slip down the stereocilium’s actin cytoskeleton. The reduced tension in the tip link permits the channel to reclose in the process of adaptation (right diagram).
Figure 2
Figure 2
Characteristics of the ear's active process (A) An input-output relation for the mammalian cochlea relates the magnitude of vibration at a specific position along the basilar membrane to the frequency of stimulation at a particular intensity. Amplification by the active process renders the actual cochlear response (red) over one-hundredfold as great as the passive response (blue). Note the logarithmic scales in this and the subsequent panels. (B) As a result of the active process, the observed basilar-membrane response (red) is far more sharply tuned to a specific frequency of stimulation, the natural frequency, than is a passive response driven to the same peak magnitude by far stronger stimulation (blue). (C) Each time the amplitude of stimulation is increased tenfold, the passive response distant from the natural frequency grows by an identical amount (green arrows). For the natural frequency at which the active process dominates, however, the maximal response of the basilar membrane increases by only 103, a factor of about 2.15 (orange arrowheads). This compressive nonlinearity implies that the basilar membrane is far more sensitive than a passive system at low stimulus levels, but approaches the passive level of responsiveness as the active process saturates for loud sounds. (D) The fourth characteristic of the active process is spontaneous otoacoustic emission, the unprovoked production of one or more pure tones by the ear in a very quiet environment. For humans and many other species, the emitted sounds differ between individuals and from ear to ear but are stable over months or even years.
Figure 3
Figure 3
Properties and consequences of the Hopf bifurcation A dynamical system that undergoes a Hopf bifurcation can be described by the relation dzdt=μz+iω0z−|z|2z, in which z is a complex variable that represents hair-bundle or basilar-membrane motion. The nature of the system's responses can be appreciated by evaluating successively the contributions of the three terms on its right side. (A) The real part of the solution for the simplified equation with only the initial term on the right displays exponential decay for negative values of the control parameter μ or exponential growth for positive values. (B) Including only the second term on the right leads to solutions that are sine and cosine waves at the natural frequency ω0. (C) Combination of the initial two terms produces oscillatory solutions that decline or grow exponentially. (D) For positive values of the control parameter, the complete equation yields spontaneous limit-cycle oscillation at the natural frequency ω0. This unforced activity may underlie spontaneous otoacoustic emission. The final term on the right has the effect of arresting the exponential growth of the response, thereby limiting the oscillation to a fixed amplitude. (E) The characteristics of the active process, as shown in the three subsequent panels, emerge from driving a system that undergoes a Hopf bifurcation with stimuli of relative amplitudes 1, 10, and 100 units (top to bottom). (F) When the dynamical system operates far from the bifurcation, its passive responses at the natural frequency are nearly linear reflections of the three stimuli. (G) When functioning near the Hopf bifurcation and stimulated at the natural frequency, the same system displays profound amplification of the smallest input and moderate amplification of the middle one. The lesser degree of amplification of successively greater stimuli represents a compressive nonlinearity: successive tenfold increments in input evoke only 2.3-fold increases in output. (H) Even at the bifurcation, the system's tuning is evident from the weak amplification of stimuli whose frequency differs from the natural frequency ω0. As for the previous panel, μ = −0.001.
Figure 4
Figure 4
Active hair-bundle motility (A) The movement of a hair bundle is measured by a using a photodiode to detect the displacement of a flexible glass fiber whose tip is attached to the bundle's top. In the absence of stimulation, the hair bundle undergoes irregular oscillations (beginning and end of upper trace) that may underlie the phenomenon of spontaneous otoacoustic emission. When a sinusoidal stimulus of ±10 nm is applied at the fiber's base (lower trace), the hair bundle responds with phase-locked oscillations roughly twice as large; the horizontal green lines demarcate the magnitude of stimulation. This enhanced movement is one indication of a hair bundle's ability to conduct mechanical amplification. (B) A graph of the sensitivity of a bundle's response as a function of stimulus frequency demonstrates the tuning of the active process. The data points have been fitted by a theoretical relation (red) that characterizes a Hopf oscillator. The hair cells of the frog's sacculus, on which these experiments were conducted, are sensitive to relatively low-frequency seismic and acoustic stimuli. (C) A doubly logarithmic plot of mechanical sensitivity as a function of stimulus amplitude discloses three regimes of responsiveness at the hair cell's natural frequency. Near threshold, the sensitivity varies almost linearly with the magnitude of stimulation (horizontal blue line at left), but the tiny responses are noisy. For stimuli exceeding 100 nm in amplitude, the responsiveness again approaches linearity as the active process saturates (horizontal blue line at right). Over the intervening range of stimulation, which corresponds to everyday acoustic stimuli, the relation displays power-law behavior with an exponent of −2/3 (oblique red line). This compressive nonlinearity, which is highly consistent for these eight hair bundles, is characteristic of a Hopf bifurcation.
Figure 5
Figure 5
Negative hair-bundle stiffness (A) The mechanical properties of a hair bundle are assessed by connecting its top to the tip of a glass stimulus fiber 100 µm in length. When a piezoelectrical stimulator displaces the base of the fiber (blue arrow at left), the bundle moves through a lesser distance owing to its stiffness (pink arrow at right). Here the movements have been exaggerated about one-hundredfold. By measuring the fiber's flexion and knowing its elasticity, an experimenter can deduce the force exerted by the hair bundle. In a displacement-clamp experiment, negative feedback holds the bundle in a commanded position while the corresponding force is recorded. (B) The displacement-force relation obtained from a spontaneously oscillating hair bundle (blue points and fitted red curve) differs strikingly from that of a linearly elastic object that obeys Hooke's Law (dashed purple line). Over the range of positions between the green arrowheads, the hair bundle displays negative stiffness; the unrestrained bundle cannot remain in this region, but must leap spontaneously in the positive or negative direction. (C) The coordinated gating of mechanoelectrical-transduction channels explains the hair bundle's negative stiffness. In this representation, three channels from distinct stereocilia are depicted in a common membrane in the interest of compactness (first diagram). When a constant force F is applied to the parallel array of channels, the three gating springs are stretched to an identical extent (second diagram). As one channel opens, the movement of its gate partially relaxes the associated gating spring (third diagram). Because the gating springs for the two remaining channels consequently bear additional tension, either of those channels is more likely to open as well (fourth diagram). This phenomenon continues until all three channels have opened (fifth diagram). The system is bistable: it can dwell in a configuration in which no channels are open or one in which all are ajar, but is unstable at the intermediate positions.
Figure 6
Figure 6
Possible mechanisms of Ca2+-induced reclosure of transduction channels When mechanical stimulation tenses the tip link, a transduction channel opens as shown in the central diagram. (A) Ca2+ entering through an open transduction channel might bind to some component of the channel itself; the binding energy would then close the channel's gate. This arrangement would have the effect of increasing the tension in the associated tip link. (B) If the transduction channel is a member of the TRP family, it might be anchored by ankyrin repeats whose relaxation in the presence of Ca2+ would allow the channel to slip downward, reducing the tension in the tip link and thus closing the channel. (C) Ca2+ might diminish the probability that myosin-1c molecules are bound to cytoskeletal actin filaments, thus allowing the transduction element to move downward and the channel to reclose. (D) The accumulation of Ca2+ might reduce tip-link tension by favoring a backward step by myosin-1c molecules. (E) The binding of Ca2+ to calmodulin molecules adorning the IQ domains might relax the neck region of myosin-1c molecules and thereby allow the channel to move downward. Because the myosin heads would not detach from actin filaments in the last two instances, those mechanisms could potentially underlie the active process even at high stimulus frequencies.
Figure 7
Figure 7
The mechanism of amplification by active hair-bundle motility Two simulations depict the responses of hair bundles to 80-Hz sinusoidal stimulus forces that produce hair-bundle displacements of ±5.7 nm. The color coding in each panel distinguishes successive phases of the simulation. To obtain the response from a passive hair bundle (left) requires a stimulus force of ±3 pN, whereas the active hair bundle (right) needs only ±0.1 pN. In this example, then, the active process confers an amplification of 30X. The open probability of the transduction channels correspondingly varies between 0.3 to 0.7 in the presence of the active process, but changes by only 0.1% in the passive circumstance. Because the hair bundles follow similar trajectories in both the passive and the active instances, the temporal traces of the hairbundle velocity are similar. Plots of the drag force, which is proportional to bundle velocity, also show nearly identical responses for the two conditions. The cartoons indicate that movement of the bundle toward the right, the positive direction, is associated with a drag force in the opposite direction (red arrows). Leftward bundle motion conversely elicits a drag force toward the right (green arrow). The five small graphs, which display the successive relations between drag force (F) and hair-bundle position (X), reveal that the passive and active responses both follow clockwise trajectories indicative of energy dissipation. For the passive hair bundle, the force applied through two types of elastic elements, the gating springs and the stereociliary pivots, is quite large. The cartoons show that extreme deflection to the right evokes a maximal elastic restoring force to the left (orange arrow), whereas peak displacement to the left elicits the greatest rightward force (blue arrow). The force-displacement graphs below the cartoons indicate that the passive hair bundle displays linear elasticity: the restoring force follows Hooke's law. Despite its magnitude, the force applied through elastic elements is out of phase with the drag force and cannot cancel it. The stimulus must therefore supply at least 7 zJ of energy during each cycle of oscillation to overcome viscous dissipation. Although the displacement of the active hair bundle closely resembles that for the passive bundle, the active process greatly alters the magnitude, and especially the timing, of the force applied through elastic elements. As the cartoon demonstrates, the greatest force to the right occurs as the hair bundle moves most quickly in that direction (red arrows), and the strongest force to the left arises during the fastest leftward motion (green arrow). The graphs beneath the cartoons reveal how this result emerges from the two components of the active process. First, adaptation continuously shifts the forcedisplacement relation back-and-forth (colored curves). And second, each excursion across the unstable region of negative stiffness speeds the hair bundle's motion. As a consequence, the operating point describes a counterclockwise trajectory nearly equal and opposite that of the drag force. In other words, whereas for the passive hair bundle the force delivered through elastic elements is in phase with bundle displacement, for the active bundle the corresponding force in in phase with bundle velocity. The stimulus does almost no work because the active process delivers an amount of energy equivalent to that lost to drag. The active process thus acts as "negative viscosity," countering the inevitably dissipative effect of the viscous medium through which the hair bundle moves. The equations used in the simulations are those of Martin et al.(2003).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Ademek N, Coluccio LM, Geeves MA. Calcium sensitivity of the cross-bridge cycle of Myolc, the adaptation motor in the inner ear. Proc. Natl. Acad. Sci. USA. 2008;105:5710–5715. - PMC - PubMed
    1. Albert JT, Nadrowski B, Gopfert MC. Mechanical signatures of transducer gating in the Drosophila ear. Curr. Biol. 2007;17:1000–1006. - PubMed
    1. Allen JB, Fahey PF. Using acoustic distortion products to measure the cochlear amplifier gain on the basilar membrane. J. Acoust. Soc. Am. 1992;92:178–188. - PubMed
    1. Art JJ, Crawford AC, Fettiplace R, Fuchs PA. Efferent regulation of hair cells in the turtle cochlea. Proc. Roy. Soc. Lond B. 1982;216:377–384. - PubMed
    1. Ashmore J. Cochlear outer hair cell motility. Physiol. Rev. 2008;88:173–210. - PubMed

Publication types

LinkOut - more resources