Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Aug 22;4(8):e1000153.
doi: 10.1371/journal.pcbi.1000153.

Structure and dynamics of interphase chromosomes

Angelo Rosa  1 , Ralf Everaers
Affiliations

Structure and dynamics of interphase chromosomes

Angelo Rosa et al. PLoS Comput Biol. .

Abstract

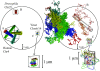
During interphase chromosomes decondense, but fluorescent in situ hybridization experiments reveal the existence of distinct territories occupied by individual chromosomes inside the nuclei of most eukaryotic cells. We use computer simulations to show that the existence and stability of territories is a kinetic effect that can be explained without invoking an underlying nuclear scaffold or protein-mediated interactions between DNA sequences. In particular, we show that the experimentally observed territory shapes and spatial distances between marked chromosome sites for human, Drosophila, and budding yeast chromosomes can be reproduced by a parameter-free minimal model of decondensing chromosomes. Our results suggest that the observed interphase structure and dynamics are due to generic polymer effects: confined Brownian motion conserving the local topological state of long chain molecules and segregation of mutually unentangled chains due to topological constraints.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

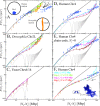
Figure 1
Figure 1. Experimental FISH data for spatial distances R 2(|N 2−N 1|) between targeted chromosome sites compared to the estimates based on the WLC model (A) and results from our simulations (B–F).
Brown ○: Saccharomyces cerevisiae Chr6 and Chr14 . Blue ○ and ◊: Homo Sapiens Chr4, |N 2−N 1|<4.5 Mbp and |N 2−N 1|>4.5 Mbp, respectively . Orange and green ○: Drosophila melanogaster Chr2L, DS5 and DS1 embryos respectively . DS5 and DS1 are two phases of cell cycle. DS1 appears later. Black continuous line: Mean-square internal distances predicted by the WLC model, Equation 1. (A) Black dashed line: Mean-square internal distances of an ideal polymer chain inside a spherical nucleus of 5 µm radius . (The exact probability distribution function of the square internal distances R 2(|N 2−N 1|) of a polymer without self-interactions obeys diffusion equation with null boundary conditions (in our case the boundary is the sphere which models the nucleus).)While data for Chr4 and Chr2L show a reasonable agreement at short-length scales, the apparent large-length scale Chr4 behavior L 2/3 contrasts with the observed L 2 for Chr2L. The insets show two schematic drawings of the Chr4 territory in a human nucleus (blue) and of Chr2L in Rabl phase in a Drosophila nucleus (orange). (B–E) Gray lines represent internal distances in the initial, “metaphase-like” chromosome configuration (Materials and Methods). Internal distances in simulated chromosomes have been averaged over 3 time windows of exponentially growing size: 240 s<t<2,400 s (dark red line), 2,400 s<t<24,000 s (magenta line) and 24,000 s<t<240,000 s (cyan line). Since yeast chromosomes rapidly equilibrate only averages over the first 24,000 s are here reported (panel C). In panel E, N 1 = 0, i.e., has been fixed at the origin of the chain to make equilibration of the chain ends evident. (F) Data from simulations of three ring polymers of decreasing half-size L c = 97.2, 48.6, and 2.7 Mbp (green, magenta and red lines respectively). Mean distances seem to extrapolate to an effective power law ∼L 2/3. Inset: Initial (left) and final (right) conformation of a (randomly chosen) half of the largest (2×97.2 Mbp) simulated ring chromosome.
Figure 2
Figure 2. Time behavior of the msd of the six inner beads (g 1(t), continuous lines), compared to the average square gyration radius (horizontal dashed lines) of the whole chromosome and measurements of the msd of the active GAL gene inside in vivo yeast nuclei (purple dots).
For comparison, g 1(t) for yeast chromosomes without topological constraints has been shown (cyan line). On short time scales, our model reproduces the typical dynamics of semi-flexible polymers with g 1(t)∼t 0.75 . For the model with constraints, there is no extended Rouse regime due to the insufficient separation of Kuhn and entanglement length. Nevertheless, we observe the characteristic g 1(t)∼t 0.25 regime for entangled, flexible polymers .
Figure 3
Figure 3. Initial (“metaphase-like”, left) and final (right) configurations of human Chr4 (A), of Drosophila Chr2L (B) and of yeast Chr6 and Chr14 (C) shown together with the spherical nucleus (black circle) of 10 µm in diameter and the corresponding simulation boxes (in black).
For the blue configuration in A and for the configuration B, we have highlighted in red the two terminal parts up to 4.5 Mbp. In Chr4, this corresponds to the terminal 4p16.3 region . (A) Simultaneous decondensation of 4 model chromosomes half the size the human Chr4. (B) Decondensation of 1 model chromosome the size the Drosophila Chr2L. The final elongated shape qualitatively resembles a Rabl-like territory. (C) Simultaneous decondensation of 6 model chromosomes the size the yeast Chr6 and Chr14. Arrows points at magnified versions of the same configurations. Lack of chromosome territoriality is evident.
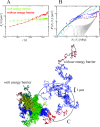
Figure 4
Figure 4. Human Chr4 territories are less stable if the energy barrier against chain crossing is switched off.
The swelling from the initial “metaphase” configuration is monitored through the time behavior of the gyration radius formula image , where rl(t) is the position vector of the lth bead and r cm(t) is the center of mass of the configuration at time t. Without barrier, chromosomes swell easier and have larger size (green and red lines, (A)). Comparison amongst internal distances between two sites located at N 1 and N 2 Mbp from one chosen end of the fiber and avalaible experimental data reflects this behavior (B). We have averaged over 3 time windows of exponentially growing size: 240 s<t<2,400 s (dark red line), 2,400 s<t<24,000 s (magenta line) and 24,000 s<t<240,000 s (cyan line). In particular, we notice that the fortuitous agreement of the magenta line with the data is lost due to the fast relaxation to equilibrium. The gray line corresponds to internal distances in the initial configuration. As expected (C), the final configuration of human Chr4 without energy barrier occupies a larger volume and is more random-walk-like than the ones where the energy barrier has been included.
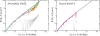
Figure 5
Figure 5. Mean square spatial distances R 2(|N 2−N 1|) between a site of the fiber located at N 2 Mbp from one chosen end of the chain and the end (here located at N 1 = 0): comparison between simulated and the avalaible experimental data on Drosophila Chr2L (left) and yeast Chr6 and Chr14 (right).
Gray lines represent internal distances in the initial, “metaphase-like” chromosome configuration (Materials and Methods). Internal distances have been averaged over 3 time windows of exponentially growing size: 240 s<t<2,400 s (dark red line), 2,400 s<t<24,000 s (magenta line) and 24,000 s<t<240,000 s (cyan line). Since yeast chromosomes rapidly equilibrate only averages over the first 24,000 s are here reported. The black continuous line is the plot of the average internal distances predicted by the WLC model, Equation 1.
Figure 6
Figure 6. Three dimensional spatial trajectories of the centers of mass of the 4 simulated human Chr4.
The color code used corresponds to the snapshots A shown in Figure 2. Motion resembles confined diffusion.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Alberts B, et al. Molecular Biology of the Cell. 4th edition. New York: Garland Science; 2002.
    1. Rabl C. Über Zellteilung. Morph Jb. 1885;10:214–330.
    1. Cremer T, Cremer C. Rise, fall and resurrection of chromosome territories: a hystorical perspective. Part I. The rise of chromosome territories. Eur J Histochem. 2006;50:161–176. - PubMed
    1. Meaburn KJ, Misteli T. Chromosome territories. Nature. 2007;445:379–381. - PubMed
    1. Haber JE, Leung WY. Lack of chromosome territoriality in yeast: promiscuous rejoining of broken chromosome ends. Proc Natl Acad Sci U S A. 1996;93:13949–13954. - PMC - PubMed

LinkOut - more resources