Geometric interpretation of gene coexpression network analysis
- PMID: 18704157
- PMCID: PMC2446438
- DOI: 10.1371/journal.pcbi.1000117
Geometric interpretation of gene coexpression network analysis
Abstract
THE MERGING OF NETWORK THEORY AND MICROARRAY DATA ANALYSIS TECHNIQUES HAS SPAWNED A NEW FIELD: gene coexpression network analysis. While network methods are increasingly used in biology, the network vocabulary of computational biologists tends to be far more limited than that of, say, social network theorists. Here we review and propose several potentially useful network concepts. We take advantage of the relationship between network theory and the field of microarray data analysis to clarify the meaning of and the relationship among network concepts in gene coexpression networks. Network theory offers a wealth of intuitive concepts for describing the pairwise relationships among genes, which are depicted in cluster trees and heat maps. Conversely, microarray data analysis techniques (singular value decomposition, tests of differential expression) can also be used to address difficult problems in network theory. We describe conditions when a close relationship exists between network analysis and microarray data analysis techniques, and provide a rough dictionary for translating between the two fields. Using the angular interpretation of correlations, we provide a geometric interpretation of network theoretic concepts and derive unexpected relationships among them. We use the singular value decomposition of module expression data to characterize approximately factorizable gene coexpression networks, i.e., adjacency matrices that factor into node specific contributions. High and low level views of coexpression networks allow us to study the relationships among modules and among module genes, respectively. We characterize coexpression networks where hub genes are significant with respect to a microarray sample trait and show that the network concept of intramodular connectivity can be interpreted as a fuzzy measure of module membership. We illustrate our results using human, mouse, and yeast microarray gene expression data. The unification of coexpression network methods with traditional data mining methods can inform the application and development of systems biologic methods.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
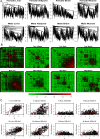




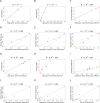

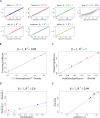
 (Equation 37); here each dot corresponds to a module. Since the grey dot corresponds to genes outside of properly defined modules, we have excluded it from the calculation of the squared correlation R
2. (D) Illustrating
(Equation 37); here each dot corresponds to a module. Since the grey dot corresponds to genes outside of properly defined modules, we have excluded it from the calculation of the squared correlation R
2. (D) Illustrating  (Equation 40); (E) Illustrating
(Equation 40); (E) Illustrating  (Equation 38). A reference line (red) with intercept 0 and slope 1 has been added to each plot. The blue line is the regression line through the points representing proper modules (i.e., the grey, non-module genes are left out). A robustness analysis with regard to different network construction methods, e.g., β>1, can be found in Text S1.
(Equation 38). A reference line (red) with intercept 0 and slope 1 has been added to each plot. The blue line is the regression line through the points representing proper modules (i.e., the grey, non-module genes are left out). A robustness analysis with regard to different network construction methods, e.g., β>1, can be found in Text S1.
Similar articles
-
Understanding network concepts in modules.BMC Syst Biol. 2007 Jun 4;1:24. doi: 10.1186/1752-0509-1-24. BMC Syst Biol. 2007. PMID: 17547772 Free PMC article.
-
WGCNA: an R package for weighted correlation network analysis.BMC Bioinformatics. 2008 Dec 29;9:559. doi: 10.1186/1471-2105-9-559. BMC Bioinformatics. 2008. PMID: 19114008 Free PMC article.
-
Differential Coexpression Network Analysis for Gene Expression Data.Methods Mol Biol. 2018;1754:155-165. doi: 10.1007/978-1-4939-7717-8_9. Methods Mol Biol. 2018. PMID: 29536442
-
Techniques for clustering gene expression data.Comput Biol Med. 2008 Mar;38(3):283-93. doi: 10.1016/j.compbiomed.2007.11.001. Epub 2007 Dec 3. Comput Biol Med. 2008. PMID: 18061589 Review.
-
From microarray to biological networks: Analysis of gene expression profiles.Methods Mol Biol. 2006;316:35-48. doi: 10.1385/1-59259-964-8:35. Methods Mol Biol. 2006. PMID: 16671399 Review.
Cited by
-
Novel structural co-expression analysis linking the NPM1-associated ribosomal biogenesis network to chronic myelogenous leukemia.Sci Rep. 2015 Jul 24;5:10973. doi: 10.1038/srep10973. Sci Rep. 2015. PMID: 26205693 Free PMC article.
-
Gene expression variability in human hepatic drug metabolizing enzymes and transporters.PLoS One. 2013 Apr 23;8(4):e60368. doi: 10.1371/journal.pone.0060368. Print 2013. PLoS One. 2013. PMID: 23637747 Free PMC article.
-
Precision machine learning to understand micro-RNA regulation in neurodegenerative diseases.Front Mol Neurosci. 2022 Sep 9;15:914830. doi: 10.3389/fnmol.2022.914830. eCollection 2022. Front Mol Neurosci. 2022. PMID: 36157078 Free PMC article. Review.
-
Comparative Transcriptomics and Co-Expression Networks Reveal Tissue- and Genotype-Specific Responses of qDTYs to Reproductive-Stage Drought Stress in Rice (Oryza sativa L.).Genes (Basel). 2020 Sep 24;11(10):1124. doi: 10.3390/genes11101124. Genes (Basel). 2020. PMID: 32987927 Free PMC article.
-
Gene co-expression network analysis of the human gut commensal bacterium Faecalibacterium prausnitzii in R-Shiny.PLoS One. 2022 Nov 18;17(11):e0271847. doi: 10.1371/journal.pone.0271847. eCollection 2022. PLoS One. 2022. PMID: 36399439 Free PMC article.
References
-
- Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabasi AL. Hierarchical organization of modularity in metabolic networks. Science. 2002;297:1551–1555. - PubMed
-
- Ihmels J, Bergmann S, Barkai N. Defining transcription modules using large-scale gene expression data. Bioinformatics. 2004;20:1993–2003. - PubMed
-
- Barabasi AL, Oltvai ZN. Network biology: understanding the cell's functional organization. Nat Rev Genet. 2004;5:101–113. - PubMed
-
- Albert R. Scale-free networks in cell biology. J Cell Sci. 2005;118:4947–4957. - PubMed
-
- Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, et al. Network motifs: simple building blocks of complex networks. Science. 2002;298:824–827. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Research Materials

