Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Apr 25;4(4):e1000028.
doi: 10.1371/journal.pcbi.1000028.

Dimensionality and dynamics in the behavior of C. elegans

Greg J Stephens  1 , Bethany Johnson-Kerner, William Bialek, William S Ryu
Affiliations

Dimensionality and dynamics in the behavior of C. elegans

Greg J Stephens et al. PLoS Comput Biol. .

Abstract

A major challenge in analyzing animal behavior is to discover some underlying simplicity in complex motor actions. Here, we show that the space of shapes adopted by the nematode Caenorhabditis elegans is low dimensional, with just four dimensions accounting for 95% of the shape variance. These dimensions provide a quantitative description of worm behavior, and we partially reconstruct "equations of motion" for the dynamics in this space. These dynamics have multiple attractors, and we find that the worm visits these in a rapid and almost completely deterministic response to weak thermal stimuli. Stimulus-dependent correlations among the different modes suggest that one can generate more reliable behaviors by synchronizing stimuli to the state of the worm in shape space. We confirm this prediction, effectively "steering" the worm in real time.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

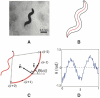
Figure 1
Figure 1. Describing the shapes of worms.
(A) Raw image in the tracking microscope. (B) The curve through the center of the body. The black circle marks the head. (C) Distances along the curve (arclength s) are measured in normalized units, and we define the tangent formula image(s) and normal formula image(s) to the curve at each point. The tangent points in a direction θ(s), and variations in this angle correspond to the curvature κ(s) = dθ(s)/ds. (D) All images are rotated so that 〈θ〉 = 0; therefore θ (s) provides a description of the worm's shape that is independent of our coordinate system, and intrinsic to the worm itself.
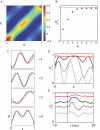
Figure 2
Figure 2. Covariance of shape fluctuations and eigenworms.
(A) The covariance matrix of fluctuations in angle C(s, s′). The inhomogeneity along the diagonal shows that the normal modes of the motion are not sinusoidal but the smooth structure of C(s, s′) means that a small number of modes are significant. (B) We find the eigenvalues of C(s, s′) and compute σ 2 K, the fraction of the total variance (integrated along the body of the worm) captured by keeping K modes (see Materials and Methods). (C) Associated with each dominant mode is an eigenvector and we refer to these as eigenworms u μ(s). The population-mean eigenworms (red) are highly reproducible across individual worms (black). (D) The fraction of variance, σ̃ 2 K, at each point along the body curve captured by keeping K modes (K = 1 to 4, from bottom to top curve). The overall error in reconstruction of the worm body curve decreases as the number of modes increases, but does so inhomogeneously. (E) In response to strong thermal stimuli, reconstructions using the eigenworms of spontaneous crawling continue to account for most of the shape variance. Worm images are recorded at times synchronized to a heat pulse and we display σ 2 K aligned with this pulse (red line). (K = 1 to 4, from bottom to top curve).
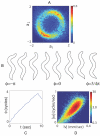
Figure 3
Figure 3. Motions along the first two eigenworms.
(A) The joint probability density of the first two amplitudes, ρ(a 1, a 2), with units such that formula image. The ring structure suggests that these modes form an oscillator with approximately fixed amplitude and varying phase φ = tan-1(-a 2/a 1). (B) Images of worms with different values of φ show that variation in phase corresponds to propagating a wave of bending along the worm’s body. (C) Dynamics of the phase φ(t) shows long periods of linear growth, corresponding to a steady rotation in the {a 1, a 2} plane, with occasional, abrupt reversals. (D) The joint density ρ(|ν|,|ω|). The phase velocity ω = dφ/dt in shape space predicts worm’s crawling speed.
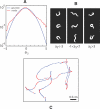
Figure 4
Figure 4. Motions along the third eigenworm.
(A) The distribution of amplitudes ρ(a 3), shown on a logarithmic scale. Units are such that formula image, and for comparison we show the Gaussian distribution; note the longer tails in ρ(a 3). (B) Images of worms with values of a 3 in the negative tail (left), the middle (center) and positive tail (right). Large negative and positive amplitudes of a 3 correspond to bends in the dorsal and ventral direction, respectively. (C) A two minute trajectory of the center of mass sampled at 4 Hz. Periods where |a 3|>1 are colored red, illustrating the association between turning and large displacements along this mode.
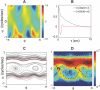
Figure 5
Figure 5. Reconstructing the phase dynamics.
(A) The mean acceleration of the phase F(ω,φ) in Equation 4. (B) The correlation function of the noise 〈η (t)η(t+τ)〉. The noise correlations are confined to short times relative to the phase velocity itself. (C) Trajectories in the deterministic dynamics. A selection of early-time trajectories is shown in black. At late times these same trajectories collapse to one of four attractors (red): forward and backward crawling and two pause states. (D) Joint density ρ(ω,φ) for worms sampled at 32 Hz. A sample trajectory of a single worm moving forwards, backwards, and pausing, is denoted by black arrows.
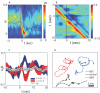
Figure 6
Figure 6. Thermal responses, mode coupling and active steering.
(A) The distribution of phase velocities ρt(ω) in response to a brief thermal stimulus. Within one second, the distribution becomes highly concentrated near ω = 0, corresponding to the pause states identified in Figure 5. (B) Correlations between phase in the {a 1,a 2} plane and a 3, formula image. Shortly after the thermal impulse (t, t′>0) the modes develop a strong anti-correlation which is distinct from normal crawling. (C) Phase dependent thermal response. Worms stimulated during ventral head swings (−2≤φ≤−1) turn dorsally (red) while worms stimulated during dorsal head swings (2≤φ≤π) turn ventrally (blue). When phase is ignored there is no discernible response (grey). Solid lines denote averages while colored bands display standard deviation of the mean. (D) Worm “steering.” A thermal impulse conditioned on the instantaneous phase was delivered automatically and repeatedly, causing an orientation change formula image in the worm's trajectory. In this example lasting 4 minutes, asynchronous impulses produced a time-averaged orientation change 〈formula image〉 = 0.01 rad/s (black), impulses at positive phase produced a trajectory with 〈formula image〉 = 0.10 rad/s (blue), and impulses at negative phase produced 〈formula image〉 = –0.12 rad/s (red). This trajectory response is consistent with the mode correlations seen in Figure 6C. We found 13 out of 20 worms produced statistically different orientation changes under stimulated and non-simulated conditions while only 1 out of 20 worms responded in the same fashion when the phase was randomized (p<0.01, Fisher exact test).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Green DM, Swets JA. New York: John Wiley & Sons; 1966. Signal Detection Theory and Psychophysics.
    1. Bolhuis J, Giraldeau L, editors. Oxford: Blackwell Publishing; 2004. The Behavior of Animals: Mechanism, Function and Evolution.
    1. Geng W, Cosman P, Baek JH, Berry C, Schafer WR. Quantitative classification and natural clustering of Caenorhabditis elegans behavioral phenotypes. Genetics. 2003;165:1117–1126. - PMC - PubMed
    1. Cronin CJ, et al. An automated system for measuring parameters of nematode sinusoidal movement. BMC Genet. 2005;6:5–24. - PMC - PubMed
    1. Hoshi K, Shingai R. Computer–driven automatic identification of locomotion states in Caenorhabditis elegans. J Neurosci Meth. 2006;157:355–363. - PubMed