Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2007 Dec;72(4):560-75.
doi: 10.1016/j.tpb.2007.08.006. Epub 2007 Aug 31.

The evolution of bet-hedging adaptations to rare scenarios

Oliver D King  1 , Joanna Masel
Affiliations

The evolution of bet-hedging adaptations to rare scenarios

Oliver D King et al. Theor Popul Biol. 2007 Dec.

Abstract

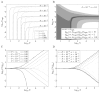
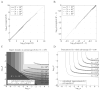
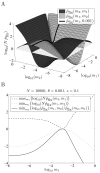
When faced with a variable environment, organisms may switch between different strategies according to some probabilistic rule. In an infinite population, evolution is expected to favor the rule that maximizes geometric mean fitness. If some environments are encountered only rarely, selection may not be strong enough for optimal switching probabilities to evolve. Here we calculate the evolution of switching probabilities in a finite population by analyzing fixation probabilities of alleles specifying switching rules. We calculate the conditions required for the evolution of phenotypic switching as a form of bet-hedging as a function of the population size N, the rate theta at which a rare environment is encountered, and the selective advantage s associated with switching in the rare environment. We consider a simplified model in which environmental switching and phenotypic switching are one-way processes, and mutation is symmetric and rare with respect to the timescale of fixation events. In this case, the approximate requirements for bet-hedging to be favored by a ratio of at least R are that sN>log(R) and thetaN>square root R .

PubMed Disclaimer

Figures

Figure 1
Figure 1
Optimal switching probabilities and the extent to which they are favored. A: The estimated optimal switching probability m̂opt is approximately θ for N larger than a threshold that increases as s decreases. Note that on the curves for θ = 0.1, m̂opt is slightly less than 0.1 even for large N, but is approximately equal to 1 − e−0.1 = 0.095. B: A broad range of switching probabilities m are only slightly disfavored relative to m̂opt when N is less than the threshold for which m̂opt ≈ θ. C and D: These graphs compare p̂fix (0, θ, N, θ, s) and p̂fix (θ, 0, N, θ, s) for a variety of s, N, and θ. For small N the switching probability m = 0 has an advantage over the switching probability m = θ, but the latter dominates for large N. (In C, the fixation probabilities for θ = ∞ were computed as π(1) and 1 – π(N – 1): the fixation probabilities of type B and type A alleles in environment F, in which they have fitness 1 + s and 1, respectively.)
Figure 2
Figure 2
Minimum conditions for bet-hedging to evolve in a finite population. R = p̂fix (0, m̂opt, N, θ, s) / p̂fix (m̂,0, N, θ, s) denotes the estimated advantage provided by using the optimal bet-hedging strategy over using no bet-hedging. A and B: When θ=3(R−1)logR/(NlogN) (from Equation 6), s = ∞, and m−1−e−θ ≈ m̂opt, the ratio p̂fix (0, m̂opt, N, θ, s) / p̂fix(m̂opt, 0, N, θ, s) , shown on the vertical axis, is approximately R. Curves in A are shown for R < N2/100, and in B for R > 1 + 10 log(N)2/N, roughly the range for which the approximation is accurate. (Note that B covers the range from R = 1.001 to R = 2.) C: Rectangular regions in which s and θ must fall to allow for a given advantage R; these are necessary but not sufficient conditions. For smaller R these rectangles are encroached on by the approximate equation for Nmin Computed estimates are shown for θ ≤ s. D: Estimated parameters θ and s for which R = 100, given as hyperbolas in log (s) and log(θ). Our computed estimates become less accurate for small sN and large θ, and are shown only for sN > 10. The curve for N = 108 is extrapolated using Equation 7.
Figure 3
Figure 3
The optimal switching probability is unique. Part A shows the surfaces of estimated fixation probabilities p̂fix(m1,m2) and p̂fix(m2, m1). Here m̂opt ≈ θ = 0.001 --- note that p̂fix (m1,0.001) ≥ p̂fix (0.001,m1) for all m1 in the interval [0, 1]. Part B shows that there is a unique optimal value: m̂opt ≈ = 0.001 is the only m2 for which p̂fix(m1, m2) ≥ p̂fix(m2, m1) for all m1 (solid line). It is also the only m2 for which p̂fix(m1, m2) ≥ 1/N for all m1 (dotted line), and the only m2 for which p̂fix (m2, m1) ≤ 1/ N for all m1 (dashed line).
Figure 4
Figure 4
Accuracy of fixation probability formula. Here we compare the approximate fixation probabilities computed with Equation 1 to Monte Carlo (MC) simulations for N = 1000. In parts A - I, θ varies by row, and s by column. The MC estimates for pfix (m, θ) and pfix (θ, m) are indicated by squares and circles respectively, and the vertical bars through these symbols indicate the standard error based on 106 trials. Equation 1 sometimes becomes inaccurate when θ and m are large, particularly for intermediate values of sN ≈ 10, for which selection is important but fairly slow. This is most noticeable in part H. Note that m̂opt ≈ θ for s = 1, but switching probabilities smaller than θ are favored for s = 0.0001. The gray shaded areas indicate the regions between p̂fix from Equation 1 and the heuristic bound for pfix described in Appendix C. The heuristic bound for pfix (m1, m2) is typically a lower-bound when m1 < m2 and an upper-bound when m2 < m1. (The shaded areas are often too narrow to be seen.)
Figure 5
Figure 5. Minimum population sizes for bet-hedging
R = p̂fix (0, m̂opt, N, θ, s) / p̂fix(m̂opt, 0, N, θ, s) denotes the estimated advantage provided by using the optimal bet-hedging strategy over using no bet-hedging. A and B: Nmin the smallest N for which R > 1 + 10−8, is approximately 2(s+1)/(sθ).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Abraham JM, Freitag CS, Clements JR, Eisenstein BI. An invertible element of DNA controls phase variation of type-1 fimbriae of Escherichia coli. Proc Natl Acad Sci U S A. 1985;82:5724–5727. - PMC - PubMed
    1. Andreadis TG. Observations on installment egg hatching in the brown salt marsh mosquito, Aedes cantator. J Am Mosq Control Assoc. 1990;6:727–729. - PubMed
    1. Avery SV. Microbial cell individuality and the underlying sources of heterogeneity. Nat Rev Micro. 2006;4:577. - PubMed
    1. Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S. Bacterial persistence as a phenotypic switch. Science. 2004;305:1622–1625. - PubMed
    1. Bell JR, Bohan DA, Shaw EM, Weyman GS. Ballooning dispersal using silk: world fauna, phylogenies, genetics and models. Bull Entomol Res. 2005;95:69–114. - PubMed

Publication types

LinkOut - more resources