Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 Jan 6;5(18):105-21.
doi: 10.1098/rsif.2007.1054.

Selective pressures for and against genetic instability in cancer: a time-dependent problem

Natalia L Komarova  1 , Alexander V Sadovsky, Frederic Y M Wan
Affiliations

Selective pressures for and against genetic instability in cancer: a time-dependent problem

Natalia L Komarova et al. J R Soc Interface. .

Abstract

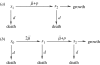
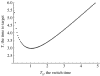
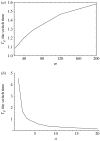
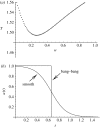
Genetic instability in cancer is a two-edge sword. It can both increase the rate of cancer progression (by increasing the probability of cancerous mutations) and decrease the rate of cancer growth (by imposing a large death toll on dividing cells). Two of the many selective pressures acting upon a tumour, the need for variability and the need to minimize deleterious mutations, affect the tumour's 'choice' of a stable or unstable 'strategy'. As cancer progresses, the balance of the two pressures will change. In this paper, we examine how the optimal strategy of cancerous cells is shaped by the changing selective pressures. We consider the two most common patterns in multistage carcinogenesis: the activation of an oncogene (a one-step process) and an inactivation of a tumour-suppressor gene (a two-step process). For these, we formulate an optimal control problem for the mutation rate in cancer cells. We then develop a method to find optimal time-dependent strategies. It turns out that for a wide range of parameters, the most successful strategy is to start with a high rate of mutations and then switch to stability. This agrees with the growing biological evidence that genetic instability, prevalent in early cancers, turns into stability later on in the progression. We also identify parameter regimes where it is advantageous to keep stable (or unstable) constantly throughout the growth.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Mutation diagrams for (a) the one-step process and (b) the two-step process.
Figure 2
Figure 2
The minimum time to target, T, for different values of the switch time, Ts. The parameters are a=2, σ=10, α=2, um=1, μ=10−7.
Figure 3
Figure 3
The switch time, Ts, as a function of parameters (a) σ and (b) a. The other parameters are a=2 and um=1 in (a), σ=10 and um=10−1 in (b), α=1.5, μ=10−5.
Figure 4
Figure 4
Does bang-bang work in the α<1 case? (a) The time to target, T, as a function of parameter w in formula (4.2). The other parameters are a=2, σ=10, α=0.5, um=1, μ=10−1. (b) The control function, u1(t), corresponding to the best value of w. Also, the best bang-bang control for these parameters is shown. The time to target for the bang-bang control is T≈1.57. For the function u1(t), it is T≈1.49.
Figure 5
Figure 5
The iterative algorithm to find the optimal control in the α<1 case. (a) The value Hi=∫0Ti|H(ui,t)|dt for consecutive iterations. (b) The iterations of the minimum time to target, T. The parameters are a=2, σ=2, α=0.5, um=1, μ=10−1.
Figure 6
Figure 6
The optimal control found by the iterative method for α<1. The optimal functions for five values of α are presented. The optimal time to target is T=1.238 for α=0.1, 1.330 for α=0.2, 1.395 for α=0.3, 1.445 for α=0.4 and 1.484 for α=0.5. The parameters are a=2, σ=2, um=1, μ=10−1.
Figure 7
Figure 7
The optimal control found by the iterative method, compared to the function u(t) found from formula (4.3), which maximizes the growth of x2(t). The parameters are a=2, α=0.5, σ=2, um=1, μ=10−1.
Figure 8
Figure 8
The optimal control found by the SQP method, for different values of α<1, for (a) a one-step process and (b) a two-step process. The other parameters are a=2, σ=10, um=1, μ=10−1.
Figure 9
Figure 9
A comparison of the optimal controls obtained for models I, II, I* and II*, with parameters a=2, σ=10, um=1, μ=0.1, α=0.5. The optimal control is plotted as a function of time.
Figure 10
Figure 10
The optimal controls u¯(t) for α<1 and various values of dm. (a) α=0.1, the optimal times to target are 4.37, 4.35, 4.28, 4.27 and 4.27 for d=1; 0.1; 0.01; 0.001 and 0.0001, respectively. (b) α=0.9, the optimal times to target are 4.36, 4.31, 4.28, 4.27 and 4.27. The other parameters are a=2, u=0.1, σ=10 and um=0.01.
Figure 11
Figure 11
The relative switching time, Ts/T, for the optimal strategy, depending on the parameters um and dm. Black corresponds to Ts/T=0 (an immediate switching) and white to Ts/T=1 (no switching). The parameters are a=2, α≥1, σ=10, μ=10−4.
Figure 12
Figure 12
The optimal time to target, T (black lines), and the corresponding switching time, Ts (grey lines), as functions of um for different values of dm. The values of log dm vary from −4 to 0, the direction of the increase of dm is indicated. The other parameters are the same as in figure 11.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. ADIFOR 1994 ADIFOR 2.0: automatic differentiation of Fortran A collaborative project between the Mathematics and Computer Science Division at Argonne National Laboratory and the Center for Research on Parallel Computation at Rice University, http://www-unix.mcs.anl.gov/autodiff/ADIFOR/.
    1. Artandi S.E, DePinho R.A. A critical role for telomeres in suppressing and facilitating carcinogenesis. Curr. Opin. Genet. Dev. 2000;10:39–46. doi: 10.1016/S0959-437X(99)00047-7. - DOI - PubMed
    1. Bailey S.M, Murnane J.P. Telomeres, chromosome instability and cancer. Nucleic Acids Res. 2006;34:2408–2417. doi: 10.1093/nar/gkl303. - DOI - PMC - PubMed
    1. Bardelli A, Cahill D.P, Lederer G, Speicher M.R, Kinzler K.W, Vogelstein B, Lengauer C. Carcinogen-specific induction of genetic instability. Proc. Natl Acad. Sci. USA. 2001;98:5770–5775. doi: 10.1073/pnas.081082898. - DOI - PMC - PubMed
    1. Bartkova J, et al. DNA damage response as a candidate anti-cancer barrier in early human tumorigenesis. Nature. 2005;434:864–870. doi: 10.1038/nature03482. - DOI - PubMed

Publication types