Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2005 Dec 27;102(52):18956-61.
doi: 10.1073/pnas.0508234102. Epub 2005 Dec 15.

Ribosome exit tunnel can entropically stabilize alpha-helices

Guy Ziv  1 , Gilad Haran, D Thirumalai
Affiliations

Ribosome exit tunnel can entropically stabilize alpha-helices

Guy Ziv et al. Proc Natl Acad Sci U S A. .

Abstract

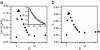
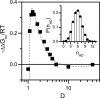
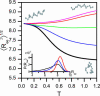
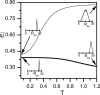
Several experiments have suggested that newly synthesized polypeptide chains can adopt helical structures deep within the ribosome exit tunnel. We hypothesize that confinement in the roughly cylindrical tunnel can entropically stabilize alpha-helices. The hypothesis is validated by using theory and simulations of coarse-grained off-lattice models. The model helix, which is unstable in the bulk, is stabilized in a cylindrical cavity provided the diameter (D) of the cylinder exceeds a critical value D*. When D < D* both the helical content and the helix-coil transition temperature (T(f)) decrease abruptly. Surprisingly, we find that the stability of the alpha-helix depends on the number (N) of amino acid residues. Entropic stabilization, as measured by changes in T(f), increases nonlinearly as N increases. The simulation results are in quantitative agreement with a standard helix-coil theory that takes into account entropy cost of confining a polypeptide chain in a cylinder. The results of this work are in qualitative accord with most of the findings of a recent experiment in which N-dependent ribosome-induced helix stabilization of transmembrane sequences was measured by fluorescence resonance energy transfer.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
Confinement effects on conformational entropy of a polypeptide chain. In the coiled state, confining the peptide to a cylinder of diameter D << RF (where RF is the Flory radius) excludes many configurations shown as gray lines. On the other hand, the rigid α-helix for which D « lp (where lp is the α-helix persistence length) loses only a few conformations, which makes the loss in entropy much smaller.
Fig. 2.
Fig. 2.
Confinement-induced α-helix formation. (a) Change of mean helical content 〈θ 〉 of an N = 16 helix model relative to mean helical content in the bulk 〈θ 〉B, as a function of cylinder diameter at T = 0.5 (≈300 K). For D > 1.3 〈θ 〉 is larger than in the bulk, i.e., the α-helix is stabilized by the cylinder. Below D ≈ 1.3, 〈θ 〉 decreases sharply. (Inset) Temperature dependence of 〈θ 〉 in the bulk (thick line) and in cylinders of diameter D = 3, 2, 1.4 (thin lines, bottom to top). (b) The folding temperature Tf as a function of D. Tf increases remarkably up to D ≈ 1.3. Arrow indicates folding temperature in the bulk.
Fig. 3.
Fig. 3.
Helix stabilization is entropic in nature. The change in the Gibbs free energy difference between helix and coil states, ΔΔGhc, as a function of D at T = 0.5. α-Helix formation is favored when D is larger than the diameter of the native helix (≈1.3). For smaller D the helix state cannot fit within the cylinder, and ΔGhc increases sharply. For D < 1 helix does not form even at T = 0. Dashed line is a fit to Eq. 4 with fitted parameters α0 = 3.9 ± 0.2, f = 0.778 ± 0.005, and lp = 230 ± 72. (Inset) Comparison of measured (bars) and calculated (circles) probability distributions of helical dihedral angles P(nHD) in a cylinder with D = 1.4. Circles are calculated by fitting Eq. 8 to the simulation data obtaining s = 1.28 ± 0.01.
Fig. 4.
Fig. 4.
Confinement-induced α-helix formation is length-dependent. (a) The mean helical content 〈θ 〉, calculated for D = 1.4 and T = 0.5 relative to the bulk value, 〈θ 〉B, increases with N. (b) Change of folding temperature ΔTf upon confinement in a cylinder of D = 1.4 at T = 0.5. In the bulk Tf ≈ 0.48 for all peptides. Dashed lines are guides to the eye.
Fig. 5.
Fig. 5.
Structural transition upon confinement. The rms end-to-end distance formula image in cylindrical confinement as a function of temperature in the bulk (black line) and in cylinders of diameter D = 3 (blue), 2 (green),1.4 (red), and 1.3 (magenta). At low temperature the peptide adopts a helical conformation (drawn in the left-hand side). At the high T limit in the bulk, the peptide samples many conformations, with either small formula image (such as the conformation drawn in bottom right corner) or with ends far away (such as the conformation drawn in top right corner). For the confined peptide, only extended conformations are observed, signifying a random coil → stretch structural transition upon confinement. (Inset) The end-to-end distance distribution function, P(Ree) in the bulk (black line) and in cylinders with diameter D = 3 (blue line) and D = 1.4 (red line). The fluctuations in the end-to-end distance are suppressed as D decreases, and the distributions sharpen.
Fig. 6.
Fig. 6.
Förster energy transfer for a peptide with N = 30. The average FRET efficiency 〈E 〉, calculated from the simulations according to Eq. 10, and plotted as function of temperature in the bulk (thin line) and under confinement in a cylinder of D = 1.4 (thick line). Insets show P(Ree) at the indicated points. At low temperatures both bulk and confined peptides are helical, whereas at high temperatures the bulk peptide is a random coil with a high 〈E 〉, but the confined peptide is relatively extended, with low 〈E 〉.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Nissen, P., Hansen, J., Ban, N., Moore, P. B. & Steitz, T. A. (2000) Science 289, 920–930. - PubMed
    1. Harms, J., Schluenzen, F., Zarivach, R., Bashan, A., Gat, S., Agmon, I., Bartels, H., Franceschi, F. & Yonath, A. (2001) Cell 107, 679–688. - PubMed
    1. Milligan, R. A. & Unwin, P. N. (1986) Nature 319, 693–695. - PubMed
    1. Yonath, A., Leonard, K. R. & Wittman, H. G. (1987) Science 236, 813–816. - PubMed
    1. Gilbert, R. J. C., Fucini, P., Connell, S., Fuller, S. D., Nierhaus, K. H., Robinson, C. V., Dobson, C. M. & Stuart, D. I. (2004) Mol. Cell 14, 57–66. - PubMed

Publication types

LinkOut - more resources