Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2005 Sep;1(4):e36.
doi: 10.1371/journal.pcbi.0010036. Epub 2005 Sep 9.

A biophysical model of the mitochondrial respiratory system and oxidative phosphorylation

Daniel A Beard  1
Affiliations

A biophysical model of the mitochondrial respiratory system and oxidative phosphorylation

Daniel A Beard. PLoS Comput Biol. 2005 Sep.

Erratum in

  • PLoS Comput Biol. 2006 Jan;2(1):e8

Abstract

A computational model for the mitochondrial respiratory chain that appropriately balances mass, charge, and free energy transduction is introduced and analyzed based on a previously published set of data measured on isolated cardiac mitochondria. The basic components included in the model are the reactions at complexes I, III, and IV of the electron transport system, ATP synthesis at F1F0 ATPase, substrate transporters including adenine nucleotide translocase and the phosphate-hydrogen co-transporter, and cation fluxes across the inner membrane including fluxes through the K+/H+ antiporter and passive H+ and K+ permeation. Estimation of 16 adjustable parameter values is based on fitting model simulations to nine independent data curves. The identified model is further validated by comparison to additional datasets measured from mitochondria isolated from rat heart and liver and observed at low oxygen concentration. To obtain reasonable fits to the available data, it is necessary to incorporate inorganic-phosphate-dependent activation of the dehydrogenase activity and the electron transport system. Specifically, it is shown that a model incorporating phosphate-dependent activation of complex III is able to reasonably reproduce the observed data. The resulting validated and verified model provides a foundation for building larger and more complex systems models and investigating complex physiological and pathophysiological interactions in cardiac energetics.

PubMed Disclaimer

Conflict of interest statement

Competing interests. The author has declared that no competing interests exist.

Figures

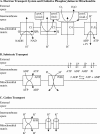
Figure 1
Figure 1. Illustration of the Components Included in the Model of Mitochondrial Oxidative Phosphorylation
(A) The major components of the electron transport system, which transfers reducing potential from NADH to oxygen, and the F1F0 ATPase, which transduces energy from proton motive force to ATP, are illustrated. Complexes I, III, and IV are labeled C1, C3, and C4, respectively. (B) The substrate transport process included in the model is shown, including the ANT and PiHt on the inner membrane, and passive permeation of ATP, ADP, AMP, and phosphate across the outer membrane. The AK reaction in the IM space is shown. (C) Transporters for hydrogen and potassium ions on the inner membrane, including K+/H+ antiporter and passive proton and potassium fluxes, are included. It is assumed that these cations rapidly equilibrate across the outer membrane.
Figure 2
Figure 2. Comparison of Model Simulations to Experimental Data on NADH, MVO2, Cytochrome C Redox, and Matrix pH for Model without Phosphate Control
(A) Results for normalized matrix NADH as a function of buffer inorganic phosphate concentration are shown for the two experimental cases of resting mitochondria ([ADP]e = 0, state 4) and active state mitochondria ([ADP]e = 1.3 mM, state 3). (B) Results for MVO2 (rate of oxygen consumption) are shown for the same experimental cases as in (A). Experimental data are not available for the resting state, in which a minimal flux through the electron transport system is maintained to compensate for cation flux across the inner membrane. (C) Results for cytochrome C reduced fraction are shown for the experimental cases as in (A). The black curves correspond to the model equations developed in the text. The red curves correspond to the best-fit model simulations obtained with equation 9 modified to not include the factor [cytC(red)2+]/cytCtot multiplying the expression for J C4. (D) Matrix pH (model-simulated and experimentally measured) is plotted as a function of buffer phosphate for the experimental cases as in (A). All computed results in this figure correspond to steady-state simulations of model described under “Mitochondrial Model without Phosphate Control.” Model simulations for [ADP]e = 1.3 mM, and [ADP]e = 0 mM are plotted as solid lines and dashed lines, respectively. Experimental data (circles and triangles) are obtained from [10].
Figure 3
Figure 3. Comparison of Model Simulations to Experimental Data on Membrane Potential for Model without Phosphate Control
The model without phosphate control is not able to fit the experimental data on mitochondrial membrane potential. Computed results in this figure correspond to steady-state simulations of the model described under “Mitochondrial Model without Phosphate Control.” Model simulations for [ADP]e = 1.3 mM, and [ADP]e = 0 mM are plotted as solid lines and dashed lines, respectively. Experimental data (circles and triangles) are obtained from [10].
Figure 4
Figure 4. Comparison of Model Simulations to Experimental Data on NADH, MVO2, Cytochrome C Redox, and Matrix pH for Model with Phosphate Control
(A) Results for normalized matrix NADH as a function of buffer inorganic phosphate concentration are shown for the two experimental cases of resting mitochondria ([ADP]e = 0, state 4) and active state mitochondria ([ADP]e = 1.3 mM, state 3). (B) Results for MVO2 (rate of oxygen consumption) are shown for the same experimental cases as in (A). (C) Results for cytochrome C reduced fraction are shown for the experimental cases as in (A). (D) Matrix pH (model-simulated and experimentally measured) is plotted as a function of buffer phosphate for the experimental cases as in (A). All computed results in this figure correspond to steady-state simulations of the model described under “Mitochondrial Model with Phosphate Control.” Model simulations for [ADP]e = 1.3 mM and [ADP]e = 0 mM are plotted as solid lines and dashed lines, respectively; experimental data are the same as plotted in Figure 2.
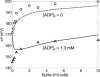
Figure 5
Figure 5. Comparison of Model Simulations to Experimental Data on Membrane Potential for Model with Phosphate Control
The model with phosphate control compares much more favorably to the experimental measurements than the model without phosphate control (see Figure 3). Computed results in this figure correspond to steady-state simulations of the model described under “Mitochondrial Model with Phosphate Control.” Model simulations for [ADP]e = 1.3 mM and [ADP]e = 0 mM are plotted as solid lines and dashed lines, respectively; experimental data are the same as plotted in Figure 3.
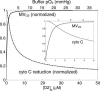
Figure 6
Figure 6. Behavior of Model at Low Oxygen Concentration
Predicted rate of oxygen consumption (MVO2) normalized to maximal rate of oxygen consumption and fraction of cytochome c reduced are plotted against oxygen concentration, which is expressed in micromoles (lower axis) and oxygen partial pressure (upper axis). The oxygen consumption curve was computed for state-3 respiration, corresponding to experimental conditions reported in [18] and [19]. The cytochrome c curve corresponds to state-4 experimental conditions reported in [17]. Inset shows predicted curves for oxygen concentrations from 0 to 5 μM.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Qian H, Beard DA, Liang SD. Stoichiometric network theory for nonequilibrium biochemical systems. Eur J Biochem. 2003;270:415–421. - PubMed
    1. Beard DA, Qian H, Bassingthwaighte JB. Stoichiometric foundation of large-scale biochemical system analysis. In: Ciabanu G, Rozenberg G, editors. Modelling in molecular biology. New York: Springer; 2004. pp. 1–20.
    1. Qian H, Beard DA. Thermodynamics of stoichiometric biochemical networks in living systems far from equilibrium. Biophys Chem. 2005;114:213–220. - PubMed
    1. Korzeniewski B. Regulation of ATP supply during muscle contraction: Theoretical studies. Biochem J. 1998;330:1189–1195. - PMC - PubMed
    1. Korzeniewski B. Regulation of ATP supply in mammalian skeletal muscle during resting state→intensive work transition. Biophysical Chemistry. 2000;83:19–34. - PubMed

Publication types