Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2005 Aug;16(8):3764-75.
doi: 10.1091/mbc.e05-04-0275. Epub 2005 Jun 1.

Tension-dependent regulation of microtubule dynamics at kinetochores can explain metaphase congression in yeast

Melissa K Gardner  1 , Chad G Pearson, Brian L Sprague, Ted R Zarzar, Kerry Bloom, E D Salmon, David J Odde
Affiliations

Tension-dependent regulation of microtubule dynamics at kinetochores can explain metaphase congression in yeast

Melissa K Gardner et al. Mol Biol Cell. 2005 Aug.

Abstract

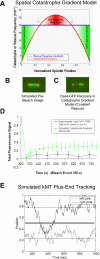
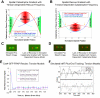
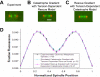
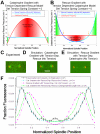
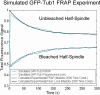
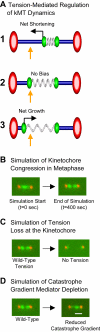
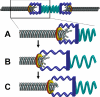
During metaphase in budding yeast mitosis, sister kinetochores are tethered to opposite poles and separated, stretching their intervening chromatin, by singly attached kinetochore microtubules (kMTs). Kinetochore movements are coupled to single microtubule plus-end polymerization/depolymerization at kinetochore attachment sites. Here, we use computer modeling to test possible mechanisms controlling chromosome alignment during yeast metaphase by simulating experiments that determine the 1) mean positions of kinetochore Cse4-GFP, 2) extent of oscillation of kinetochores during metaphase as measured by fluorescence recovery after photobleaching (FRAP) of kinetochore Cse4-GFP, 3) dynamics of kMTs as measured by FRAP of GFP-tubulin, and 4) mean positions of unreplicated chromosome kinetochores that lack pulling forces from a sister kinetochore. We rule out a number of possible models and find the best fit between theory and experiment when it is assumed that kinetochores sense both a spatial gradient that suppresses kMT catastrophe near the poles and attachment site tension that promotes kMT rescue at higher amounts of chromatin stretch.

PubMed Disclaimer

Figures

Figure 1.
Figure 1.
Position-dependent gradient models for the regulation of kMT dynamics fail to reproduce Cse4-GFP FRAP experimental results. (A) The catastrophe gradient model: kMT plus-end catastrophe frequency peaks at the spindle equator, whereas plus-end rescue frequency remains constant. (B) Representative simulated image before the bleach event using the catastrophe gradient model (kinetochore-associated Cse4-GFP, green; spindle pole body-associated Spc29-CFP, red). (C) Significant fluorescence recovery of kinetochore-associated Cse4-GFP fluorescence using the spatial catastrophe gradient model does not reproduce experimental results. (D) Representative Cse4-GFP FRAP experimental and simulated time series of fluorescence recovery. Kinetochore-associated markers in one-half-spindle were bleached and then observed over time to quantify fluorescence recovery. Because Cse4-GFP is stably bound at the kinetochore, fluorescence recovery results exclusively from redistribution of kinetochores between spindle halves. The lack of recovery observed experimentally indicates that kinetochores remain constrained to their own half-spindle throughout the experiment. Models with position-dependent catastrophe frequencies only (i.e., no tension dependence) do not limit spindle-equator crossing sufficiently to reproduce experimental results. (E) Typical simulated plus-end kMT positions at steady state using the spatial catastrophe gradient model for regulation of MT dynamics. The representative trace shows a pair of sister kMT plus ends and their movements relative to the spindle poles and the equator. Although individual kinetochores separate and oscillate on either side of the spindle equator, kinetochores frequently move into the opposite half-spindle for extended periods of time.
Figure 2.
Figure 2.
Models where kinetochores sense both spindle position to regulate kMT plus-end catastrophe frequency and tension due to chromatin stretch to regulate kMT plus-end rescue frequency successfully reproduce Cse4-GFP FRAP experimental results. Excursions of kMT plus-ends into the opposite spindle half are limited, and therefore these models quantitatively reproduce Cse4-GFP FRAP experimental results. (A) The spatial model for regulation of kMT plus-end catastrophe frequency with kMT rescue frequency regulated by tension generated via chromatin stretch between separated sister kinetochores: rescue frequencies shown are mean values calculated for a given spindle position during the simulation, because rescue frequency is directly dependent on the sister kinetochore separation distance. Dependence of kMT plus-end rescue frequency on tension between sister kinetochores is directional, such that mean rescue frequencies tend to decrease as kMTs lengthen, due to decreased separation between sister kinetochores. For this distribution, Vg = Vs = 2.0 μm/min and the spring constant is ρ* = 0.9 μm-1. Gold arrows correspond to the spindle locations of predicted peaks in kinetochore-associated Cse4-GFP fluorescence. (B) The spatial model for regulation of kMT plus-end rescue frequency with kMT catastrophe frequency regulated by tension between sister kinetochores. (C) Representative simulated images for the Cse4-GFP FRAP experiment using a model where the kinetochore senses spindle position to regulate kMT plus-end catastrophe frequency and senses tension generated via chromatin stretch to regulate kMT plus-end rescue frequency. For the model shown in A, there is negligible visible recovery in Cse4-FRAP experiment simulations, reproducing experimental results. (D) Simulated Cse4-GFP FRAP images for the model shown in B. (E) Representative Cse4-GFP FRAP experimental and simulated time series of fluorescence recovery. Models that include regulation of kMT plus-end switching frequencies based on tension between sister kinetochores reproduce experimental results. (F) Typical simulated plus-end kMT positions at steady state for the models shown in A and B. Here, equator crossing is limited, because kMT plus-ends are less likely to experience rescue events as kinetochores move closer to their sisters. Kinetochores rarely cross the equator, but remain dynamic, moving toward the spindle equator and back to the poles.
Figure 3.
Figure 3.
The models shown in Figure 2, A and B, reproduce experimental metaphase kinetochore clustering. (A) Experimental metaphase spindle image of Cse4-GFP–labeled kinetochores (green) relative to Spc29-CFP–labeled spindle poles (red). (B) Representative simulated image using the model as shown in Figure 2A. Tight kinetochore-associated fluorescence clusters are comparable with the experimental image. Bar, 1000 nm. (C) Representative simulated image using the model as shown in Figure 2B. (D) Quantitative analysis of average simulated kinetochore clustering observed via Cse4-GFP compared with mean experimental results. Simulation results reproduce experimental results for both the model shown in Figure 2A and the model in Figure 2B.
Figure 4.
Figure 4.
Experimental measurement and simulation of the kinetochore-associated fluorescence distribution in cdc6 mutant cells. (A) In a model where kinetochores regulate kMT plus-end rescue frequency by sensing tension generated through the stretch of chromatin between sister kinetochores, cdc6 mutant cells with single-kinetochore chromatin can be modeled by reducing the tension spring constant to zero and increasing simulated spindle lengths to match experimentally observed values. Gold arrows indicate the locations of predicted peaks in kinetochore-associated fluorescence. For this distribution, Vg = Vs = 1.7 μm/min and the spring constant is ρ* = 0 μm-1. (B) The tension spring constant is reduced to zero in a model where the kinetochores regulate kMT plus-end catastrophe frequency by sensing tension generated via the stretch of chromatin between sister kinetochores. (C) The experimental effect of loss of tension in Cdc6p depleted cells. Kinetochores (Cse4-GFP, green) are clustered near the poles (Spc29-CFP, red), indicating that the net kMT length is shorter in the mutant spindles compared with wild-type cells. (D) Simulated effect of loss of tension between sister kinetochores using a model where rescue frequency is regulated by tension. Kinetochores are clustered very near to the poles, qualitatively and quantitatively reproducing experimental observations of cdc6 mutant cells. Bar, 1000 nm. (E) Simulated effect of loss of tension using a model where catastrophe frequency is regulated by tension at the kinetochore. (F) Quantitative analysis of simulated kinetochore clustering compared with experimental fluorescence distribution in tension-deficient spindles. Models with increased spindle length but without tension loss do not reproduce experimental results (p < 0.01). In addition, the rescue gradient model with tension dependent catastrophe frequency fails to reproduce experimental results (p < 0.01).
Figure 5.
Figure 5.
Simulation of GFP-Tub1 FRAP experiments. Experimentally, GFP-Tub1 labeled spindles are imaged, and half-spindles are photobleached at time t = 0 (Maddox et al., 2000). FRAP of the bleached half-spindle and loss-of-fluorescence in the unbleached half-spindle are quantified experimentally and in simulations. Simulated results are compared with live cell experimental data from Maddox et al. (2000). For the simulation results shown, Vg = Vs = 2.0 μm/min and the spring constant is ρ* = 0.9 μm-1. Catastrophe and rescue frequency are modeled as shown in Figure 2A. GFP-Tub1 recovery profiles for simulated kMT dynamics qualitatively and quantitatively reproduce experimental results (p = 0.96). The average experimental time to half-maximal recovery was 52 ± 24 s (n = 6; Maddox et al., 2000), compared with a simulated half-maximal recovery time of 53 ± 15 s (n = 6).
Figure 6.
Figure 6.
Model for metaphase congression in budding yeast. For clarity, the right kinetochore is fixed at its mean position, whereas the left kinetochore moves, although both kinetochores are dynamic in simulation, each affecting the relative tension experienced by its assigned sister. Kinetochores are green, spindle pole bodies red, kMTs blue, and the cohesin/chromatin “spring” is gray. Gold arrows indicate spindle locations of predicted peaks in kinetochore-associated fluorescence. (A, 1) The left kinetochore is near to the spindle equator, under low tension, resulting in a high catastrophe and low rescue frequency for the kMT plus-end originating from the left pole. This biases the left kMT plus-end toward net depolymerization. (A, 2) The left kinetochore in the quarter spindle area with “proper” sister separation and moderate tension has equal probabilities of catastrophe and rescue at the left kMT plus-end. Therefore, the left kMT is not biased toward either growing or shrinking. (A, 3) The left kinetochore is near the left kMT spindle pole body and under high tension, resulting in a low catastrophe and high rescue frequency at the kMT plus-end. This biases the left kMT plus-end toward net polymerization. (B) Simulation of congression: from an initially random distribution of kinetochore localization at the initiation of the simulation (t = 0), the simulation results in alignment of kinetochores into a metaphase configuration within a few minutes. (C) Simulation of anaphase via loss of tension: after normal metaphase alignment, a sudden loss of tension results in simulated kinetochore movement to average positions close to the spindle poles. This is observed experimentally for Cdc6p-depleted cells and during anaphase A (Guacci et al., 1997; Straight, 1997; Pearson et al., 2001). Simulated spindle lengths were increased to match experimentally observed Cdc6p depleted spindles. (D) A representative simulated image in which a theoretical catastrophe gradient mediator molecule is depleted. Bar, 1000 nm. A threefold decrease in peak catastrophe frequency at the equator results in one focused cluster of kinetochore-associated fluorescence that stochastically moves from one spindle-half to another and transiently separates into two closely spaced clusters. Thus, a gradient in catastrophe frequency drives the separation of sister kinetochores to generate chromatin stretch.
Figure 7.
Figure 7.
A speculative mechanism for tension-dependent rescue. (A) In this hypothetical mechanism, the kinetochore sleeve (possibly formed via the Dam1/DASH complex) is pushed toward the kMT minus end via protofilament splaying during depolymerization. Simultaneous depolymerization at the sister kMT plus end tends to build tension, stretching the kinetochore (blue spring) and the chromatin (green spring). (B) As tension builds, the sleeve is pulled toward the kMT plus-end to limit protofilament splay. (C) Protofilament straightening stabilizes the tip against further depolymerization and so promotes rescue. The stabilized tip rescues and starts to polymerize.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Biggins, S., and Murray, A. W. (2001). The budding yeast protein kinase Ipl1/Aurora allows the absence of tension to activate the spindle checkpoint. Genes Dev. 15, 3118-3129. - PMC - PubMed
    1. Biggins, S., and Walczak, C. E. (2003). Captivating capture: how microtubules attach to kinetochores. Curr. Biol. 13, R449-460. - PubMed
    1. Brower-Toland, B. D., Smith, C. L., Yeh, R. C., Lis, J. T., Peterson, C. L., and Wang, M. D. (2002). Mechanical disruption of individual nucleosomes reveals a reversible multistage release of DNA. Proc. Natl. Acad. Sci. USA 99, 1960-1965. - PMC - PubMed
    1. Brown, G. C., and Kholodenko, B. N. (1999). Spatial gradients of cellular phospho-proteins. FEBS Lett. 457, 452-454. - PubMed
    1. Caplow, M., and Shanks, J. (1996). Evidence that a single monolayer tubulin-GTP cap is both necessary and sufficient to stabilize microtubules. Mol. Biol. Cell 7, 663-675. - PMC - PubMed

Publication types

MeSH terms

LinkOut - more resources