Braiding DNA: experiments, simulations, and models
- PMID: 15778439
- PMCID: PMC1305643
- DOI: 10.1529/biophysj.104.056945
Braiding DNA: experiments, simulations, and models
Abstract
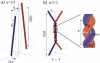
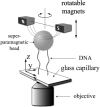
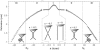
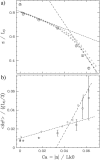
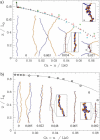
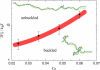
DNA encounters topological problems in vivo because of its extended double-helical structure. As a consequence, the semiconservative mechanism of DNA replication leads to the formation of DNA braids or catenanes, which have to be removed for the completion of cell division. To get a better understanding of these structures, we have studied the elastic behavior of two braided nicked DNA molecules using a magnetic trap apparatus. The experimental data let us identify and characterize three regimes of braiding: a slightly twisted regime before the formation of the first crossing, followed by genuine braids which, at large braiding number, buckle to form plectonemes. Two different approaches support and quantify this characterization of the data. First, Monte Carlo (MC) simulations of braided DNAs yield a full description of the molecules' behavior and their buckling transition. Second, modeling the braids as a twisted swing provides a good approximation of the elastic response of the molecules as they are intertwined. Comparisons of the experiments and the MC simulations with this analytical model allow for a measurement of the diameter of the braids and its dependence upon entropic and electrostatic repulsive interactions. The MC simulations allow for an estimate of the effective torsional constant of the braids (at a stretching force F = 2 pN): C(b) approximately 48 nm (as compared with C approximately 100 nm for a single unnicked DNA). Finally, at low salt concentrations and for sufficiently large number of braids, the diameter of the braided molecules is observed to collapse to that of double-stranded DNA. We suggest that this collapse is due to the partial melting and fraying of the two nicked molecules and the subsequent right- or left-handed intertwining of the stretched single strands.
Figures
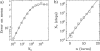

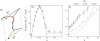


Similar articles
-
Nucleation of Multiple Buckled Structures in Intertwined DNA Double Helices.Phys Rev Lett. 2017 Nov 3;119(18):188103. doi: 10.1103/PhysRevLett.119.188103. Epub 2017 Oct 31. Phys Rev Lett. 2017. PMID: 29219598 Free PMC article.
-
Salt-dependent DNA superhelix diameter studied by small angle neutron scattering measurements and Monte Carlo simulations.Biophys J. 1998 Dec;75(6):3057-63. doi: 10.1016/S0006-3495(98)77746-X. Biophys J. 1998. PMID: 9826625 Free PMC article.
-
The influence of salt on the structure and energetics of supercoiled DNA.Biophys J. 1994 Dec;67(6):2146-66. doi: 10.1016/S0006-3495(94)80732-5. Biophys J. 1994. PMID: 7696459 Free PMC article.
-
Conformational and thermodynamic properties of supercoiled DNA.Annu Rev Biophys Biomol Struct. 1994;23:609-43. doi: 10.1146/annurev.bb.23.060194.003141. Annu Rev Biophys Biomol Struct. 1994. PMID: 7919794 Review.
-
DNA mechanics.Annu Rev Biomed Eng. 2005;7:21-53. doi: 10.1146/annurev.bioeng.6.062403.132016. Annu Rev Biomed Eng. 2005. PMID: 16004565 Review.
Cited by
-
Chiral discrimination and writhe-dependent relaxation mechanism of human topoisomerase IIα.J Biol Chem. 2013 May 10;288(19):13695-703. doi: 10.1074/jbc.M112.444745. Epub 2013 Mar 18. J Biol Chem. 2013. PMID: 23508957 Free PMC article.
-
Passive all-optical force clamp for high-resolution laser trapping.Phys Rev Lett. 2005 Nov 11;95(20):208102. doi: 10.1103/PhysRevLett.95.208102. Epub 2005 Nov 8. Phys Rev Lett. 2005. PMID: 16384102 Free PMC article.
-
Defect-facilitated buckling in supercoiled double-helix DNA.Phys Rev E. 2018 Feb;97(2-1):022416. doi: 10.1103/PhysRevE.97.022416. Phys Rev E. 2018. PMID: 29548184 Free PMC article.
-
A HaloTag Anchored Ruler for Week-Long Studies of Protein Dynamics.J Am Chem Soc. 2016 Aug 24;138(33):10546-53. doi: 10.1021/jacs.6b05429. Epub 2016 Aug 9. J Am Chem Soc. 2016. PMID: 27409974 Free PMC article.
-
Single-molecule measurements of DNA topology and topoisomerases.J Biol Chem. 2010 Jun 18;285(25):18967-71. doi: 10.1074/jbc.R109.092437. Epub 2010 Apr 9. J Biol Chem. 2010. PMID: 20382732 Free PMC article. Review.
References
-
- Adams, D., E. Shekhtman, E. Zechiedrich, M. Schmid, and N. Cozzarelli. 1992. The role of topoisomerase IV in partitioning bacterial replicons and the structure of catenated intermediates in DNA replication. Cell. 71:277–288. - PubMed
-
- Bouchiat, C., and M. Mézard. 1998. Elasticity theory of a supercoiled DNA molecules. Phys. Rev. Lett. 80:1556–1559.
-
- Bryant, Z., M. D. Stone, J. Gore, S. B. Smith, N. R. Cozzarelli, and C. Bustamante. 2003. Structural transitions and elasticity from torque measurements on DNA. Nature. 424:338–341. - PubMed
-
- Charvin, G., T. Strick, J.-F. Allemand, V. Croquette, and D. Bensimon. 2004. Twisting DNA: single molecules studies. Contemp. Phys. 45:383–403.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

