Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2004 Aug 4:5:104.
doi: 10.1186/1471-2105-5-104.

Design, implementation and evaluation of a practical pseudoknot folding algorithm based on thermodynamics

Jens Reeder  1 , Robert Giegerich
Affiliations

Design, implementation and evaluation of a practical pseudoknot folding algorithm based on thermodynamics

Jens Reeder et al. BMC Bioinformatics. .

Abstract

Background: The general problem of RNA secondary structure prediction under the widely used thermodynamic model is known to be NP-complete when the structures considered include arbitrary pseudoknots. For restricted classes of pseudoknots, several polynomial time algorithms have been designed, where the O(n6)time and O(n4) space algorithm by Rivas and Eddy is currently the best available program.

Results: We introduce the class of canonical simple recursive pseudoknots and present an algorithm that requires O(n4) time and O(n2) space to predict the energetically optimal structure of an RNA sequence, possible containing such pseudoknots. Evaluation against a large collection of known pseudoknotted structures shows the adequacy of the canonization approach and our algorithm.

Conclusions: RNA pseudoknots of medium size can now be predicted reliably as well as efficiently by the new algorithm.

PubMed Disclaimer

Figures

Figure 1
Figure 1
A simple pseudoknot. A simple pseudoknot, formed by helices a – a' and b – b', with intervening sequences u, v, w. If the internal parts u, v, w contain further secondary structures, we call it a simple recursive pseudoknot.
Figure 2
Figure 2
The boundaries of a pseudoknot. Eight moving boundaries delineating a simple recursive pseudoknot.
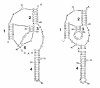
Figure 3
Figure 3
The pseudoknot of Hepatitis Delta Virus. On the left side the structure proposed by [32], on the right the MFE-structure predicted by pknotsRG. Our algorithm misses only the short helix 5 and adds 3 basepairs to helix 4. Image created with RnaViz2 [33].
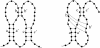
Figure 4
Figure 4
Kissing hairpins and triple helix interaction. Two examples of more complex pseudoknots with three helices: Kissing hairpins (left) and triple helix interaction (right).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Cech T. Conserved sequences and structures of group I introns: building an active site for RNA catalysis–A review. Gene. 1988;73:259–271. doi: 10.1016/0378-1119(88)90492-1. - DOI - PubMed
    1. Barette I, Poisson G, Gendron P, Major F. Pseudoknots in prion protein mRNAs confirmed by comparative sequence analysis and pattern searching. Nucleic Acids Research. 2001;29:753–758. doi: 10.1093/nar/29.3.753. - DOI - PMC - PubMed
    1. Dennis C. The brave new world of RNA. Nature. 2002;418:122–124. doi: 10.1038/418122a. - DOI - PubMed
    1. Zuker M, Sankoff S. RNA secondary structures and their prediction. Bull Math Biol. 1984;46:591–621.
    1. Hofacker I, Fontana W, Stadler P, Bonhoeffer L, Tacker M, Schuster P. Fast folding and comparison of RNA secondary structures. Monatshefte Chemie. 1994;125:167–188.

Publication types

LinkOut - more resources