Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2004 Jul 27;101(30):11030-5.
doi: 10.1073/pnas.0404206101. Epub 2004 Jul 16.

Prospects for inferring very large phylogenies by using the neighbor-joining method

Koichiro Tamura  1 , Masatoshi Nei, Sudhir Kumar
Affiliations

Prospects for inferring very large phylogenies by using the neighbor-joining method

Koichiro Tamura et al. Proc Natl Acad Sci U S A. .

Abstract

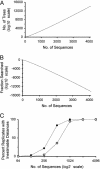
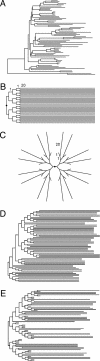
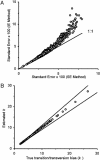
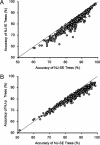
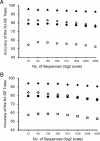
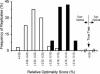
Current efforts to reconstruct the tree of life and histories of multigene families demand the inference of phylogenies consisting of thousands of gene sequences. However, for such large data sets even a moderate exploration of the tree space needed to identify the optimal tree is virtually impossible. For these cases the neighbor-joining (NJ) method is frequently used because of its demonstrated accuracy for smaller data sets and its computational speed. As data sets grow, however, the fraction of the tree space examined by the NJ algorithm becomes minuscule. Here, we report the results of our computer simulation for examining the accuracy of NJ trees for inferring very large phylogenies. First we present a likelihood method for the simultaneous estimation of all pairwise distances by using biologically realistic models of nucleotide substitution. Use of this method corrects up to 60% of NJ tree errors. Our simulation results show that the accuracy of NJ trees decline only by approximately 5% when the number of sequences used increases from 32 to 4,096 (128 times) even in the presence of extensive variation in the evolutionary rate among lineages or significant biases in the nucleotide composition and transition/transversion ratio. Our results encourage the use of complex models of nucleotide substitution for estimating evolutionary distances and hint at bright prospects for the application of the NJ and related methods in inferring large phylogenies.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
(A) Total number of possible bifurcating trees for different number of sequences. Computed by equation 5.1 of ref. . (B) Fraction of all topologies that are examined by the neighbor-joining (NJ) (2) method in producing a final tree. For a given number of sequences (m), the number of topologies explored by the NJ algorithm can be given by [m(m2 – 1)/6] – 7. This formula was derived from the observation that at each step of sequence clustering the NJ method examines mi(mi – 1)/2 trees for mi ≥ 5 (assuming that each sequence pairing in the NJ algorithm examines a distinct tree), where mi is the number of sequences at step i. For mi = 4, NJ examines all three possible trees. Because the number of sequences decreases by one in each step of sequence clustering, the total number of topologies examined is given by formula image. (C) Proportion of data sets in which the original Tamura–Nei (TN) (3) distance was not applicable for one or more pairwise comparisons for type B model trees (filled symbols) and type C model trees (open symbols) in Fig. 2. The expected maximum distance was 0.47 for 32-sequence trees and 0.61 for 4,096-sequence trees. The simulation procedure was as follows. For a given model tree, a data set of extant nucleotide sequences of n = 1,000 was generated by using the TN model with k1 = k2 = 20, gA = gT = 0.4 and gC = gG = 0.1. For each model tree, 100 data sets were generated, and the proportion of data sets in which unestimable distances occurred was computed.
Fig. 2.
Fig. 2.
Some of the model trees used in computer simulations for examining the accuracy of NJ trees. (A) A 66-sequence model tree based on the eutherian phylogeny (see ref. 24). Branches are drawn with relative lengths. (B and C) Trees with constant (model tree B) and variable (model tree C) evolutionary rates that were used to generate increasingly larger trees by connecting their copies at the roots (marked by filled circle) (see also ref. 10). (D and E) Two examples of randomly generated model trees, with equal (tree D) and unequal (tree E) exterior branch lengths. For all model trees (except in A), the expected interior branch lengths were assumed to be the same (see text for details).
Fig. 3.
Fig. 3.
Standard errors and transition/transversion rate ratios obtained by the SE method. (A) Relationships between the standard errors of evolutionary distances obtained by the IE and SE methods for a data set of 66 computer-generated sequences according to the model tree in Fig. 2 A. The TN model was used for generating sequence data with the transition/transversion rate ratios k1 and k2 = 4.4, G + C content (θ) = 0.61, and sequence length n = 1,066 nucleotides. There are (66 × 65)/2 = 2,145 data points in this figure. (B) Relationships between the estimated and true values of k (= [k1 + k2]/2) for 448 different patterns of nucleotide substitutions (see text). For each pattern of nucleotide substitution, the average value (circles) and the 95% confidence limits (lines) of the estimate of k were obtained from 100 data sets generated by computer simulation with the model tree in Fig. 2 A.
Fig. 4.
Fig. 4.
Accuracy of NJ-SE trees. (A) Accuracies (PC) of NJ trees when the SE and IE methods with the TN model were used for the 66-sequence model tree in Fig. 2 A (see text). (B) Comparison of PC values for NJ-SE trees with those for NJ trees obtained with p-distance (NJ-p). For each simulation condition, average PC values from 100 replicate simulations are plotted.
Fig. 5.
Fig. 5.
Accuracies (PC) of NJ-SE trees with increasing numbers of sequences when the TN model was used. (A) Type B and type C model trees in Fig. 2 were used. For nuclear gene evolution, k1 = k2 = 4, gA = gT = gC = gG = 0.25, and n = 1,000 were used for both type B trees (filled circles) and type C trees (filled triangles). For mitochondrial gene evolution, k1 = k2 = 20, gA = gT = 0.40, gC = gG = 0.10, and n = 1,000 were used for both type B trees (open circles) and type C trees (open triangles). (B) Type D and type E model trees in Fig. 2 were used. For nuclear gene evolution, k1 = k2 = 4, gA = gT = gC = gG = 0.25, and n = 1,000 were used for both type D trees (filled squares) and type E trees (filled diamonds). For mitochondrial gene evolution, k1 = k2 = 20, gA = gT = 0.40, gC = gG = 0.10, and n = 1,000 were used for both type D trees (open squares) and type E trees (open diamonds).
Fig. 6.
Fig. 6.
Distribution of relative optimality scores (R) of NJ-SE trees (filled bars) and NJ-IE trees (open bars) when a type B model tree (Fig. 2B) with 4,096 sequences is used. R is defined as (SNJ – ST)/ST, where SNJ and ST are the sum of all branch lengths for a NJ tree and the true tree, respectively (32). Therefore, when a NJ tree is the same as the true tree, R is 0. The sum (SNJ) of branch lengths of a NJ tree is often smaller than that of the true tree when the number of sequences is large, and R is usually negative. However, in general, the R values for NJ-SE trees are closer to 0 (R value for the true tree) than those for NJ-IE trees are. In this simulation the TN model with k1 = k2 = 4, gA = gT = gC = gG = 0.25, and n = 1,000 was used.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Nei, M. & Kumar, S. (2000) Molecular Evolution and Phylogenetics (Oxford Univ. Press, New York).
    1. Saitou, N. & Nei, M. (1987) Mol. Biol. Evol. 4, 406–425. - PubMed
    1. Tamura, K. & Nei, M. (1993) Mol. Biol. Evol. 10, 512–526. - PubMed
    1. Felsenstein, J. (2003) Inferring Phylogeny (Sinauer, Sunderland, MA).
    1. Joost, P. & Methner, A. (2002) Genome. Biol. 3, RESEARCH0063. - PMC - PubMed

Publication types