Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Comparative Study
. 2004 Jan;86(1 Pt 1):576-88.
doi: 10.1016/S0006-3495(04)74136-3.

Hydrodynamic forces applied on intercellular bonds, soluble molecules, and cell-surface receptors

Harish Shankaran  1 , Sriram Neelamegham
Affiliations
Comparative Study

Hydrodynamic forces applied on intercellular bonds, soluble molecules, and cell-surface receptors

Harish Shankaran et al. Biophys J. 2004 Jan.

Abstract

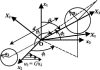
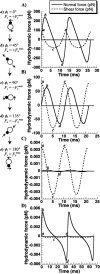
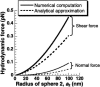
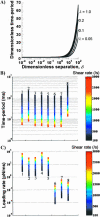
Cells and biomolecules exposed to blood circulation experience hydrodynamic forces that affect their function. We present a methodology to estimate fluid forces and force loading rates applied on cellular aggregates, cell-surface proteins, and soluble molecules. Low Reynolds-number hydrodynamic theory is employed. Selected results are presented for biological cases involving platelets, neutrophils, tumor cells, GpIb-like cell-surface receptors, and plasma von Willebrand factor (vWF)-like soluble proteins. Calculations reveal the following: 1), upon application of constant linear shear, cell aggregates and biomolecules experience time-varying forces due to their tumbling motion. 2), In comparison to neutrophil homotypic aggregates, the maximum force applied on neutrophil-platelet aggregates is approximately threefold lower. Thus, alterations in cell size may dramatically alter adhesion molecule requirement for efficient cell binding. Whereas peak forces on homotypic cell doublets are tensile, shear forces dominate in heterotypic doublets with radius ratio <0.3. 3), The peak forces on platelet GpIb and von Willebrand factor are of comparable magnitude. However, they are orders-of-magnitude lower than those applied on intercellular bonds. Charts are provided to rapidly evaluate the magnitude of hydrodynamic force and rotation time-period occurring in any given experiment. The calculation scheme may find application in studies of vascular biology and receptor biophysics.

PubMed Disclaimer

Figures

FIGURE 1
FIGURE 1
Coordinate system. Biological particles are modeled as a pair of (un)equal spheres of radii a1 and a2 (a1 > a2) separated by a rigid tether of length d. Space-fixed coordinate system is designated xi. x3 coincides with the direction of fluid flow, x2 is the direction of the velocity gradient, and x1 is the vorticity axis. The origin O lies at the midpoint of the line joining the centers of the two spheres. Xi describes the particle-fixed coordinates. X3 lies along the line joining the centers of the two spheres. It is directed toward the larger sphere. X2 is coplanar with the x1–x3 plane, and X1 is perpendicular to X2 and X3. (θ1, φ1) and (θ2, φ2) are polar and azimuthal angles with respect to the axes x1 and x2, respectively. (Figure adapted from Arp and Mason, 1977.)
FIGURE 2
FIGURE 2
Hydrodynamic force applied on cell doublets, cell-surface receptors, and soluble molecules. Cases considered are (A) PMN-PMN doublets, (B) platelet-tumor doublets, (C) platelet surface receptors, and (D) vWF-like soluble molecules. Dumbbells rotating in the x2–x3 plane (θ1 = π/2) were examined starting with the initial coordinate φ1 = 0 at t = 0. The shear rate was 600/s, fluid viscosity was 1 cP and other parameter values correspond to typical values in Table 1. The magnitude of normal (continuous line) and shear forces (dashed line) are plotted as a function of time. Cartoons (a–e) correspond to orientations of maximum shear (a, c, e), tension (b), and compression (d) during doublet half-rotation. Points corresponding to each of these orientations are labeled in the individual panels.
FIGURE 3
FIGURE 3
Normal and shear forces. (A) Normal force coefficient (αn) and (B) shear force coefficient (αs) were computed over a range of dimensionless separation distances (δ = d/a1) and radius ratios λ (= a2/a1). (C) The regions indicate the outer bounds of the normal and shear forces obtained for the following cases: 1, PMN-PMN (dark green); 2, platelet-platelet (pink); 3, PMN-platelet (blue); 4, PMN-tumor cell (red); and 5, platelet-tumor cell (orange). Regions in the inset indicate ranges of forces for these cases: 6, platelet receptors (dark blue); 7, PMN receptors (brown); and 8, soluble vWF molecule (lime). The limits on the forces were obtained by using the range of particle radii and separation distances listed in Table 1 for the hydrodynamic computations, and connecting individual points with lines. All force data are shown normalized by μG. Multiplying the values in the chart with the viscosity (in Pa/s) and the shear rate (in s−1) yields the applied force in pN. Bold black line corresponds to Fn/μG = Fs/μG.
FIGURE 4
FIGURE 4
Force applied on cell-surface receptors. Analytical approximation of the force on a receptor obtained by neglecting the disturbance velocity due to the smaller sphere (dashed line) was compared with the complete numerical computation that accounted for the hydrodynamic interaction between the two spheres (continuous line). Shear force is depicted using bold lines, whereas normal force is shown using lines of normal weight. Calculations were performed for a1 = 1.5 μm, d = 30 nm, and a2 ranging from 2 to 100 nm. Force predictions by both methods are within 10% of each other for a2 < 6 nm. At a2 = 100 nm, shear and normal force are underpredicted by 30 and 50%, respectively, when the analytical approximation is applied.
FIGURE 5
FIGURE 5
Period of rotation and dynamic force loading rates. (A) Chart for the evaluation of dimensionless period of rotation (TG/2π) for a range of δ- and λ-values. The chart in A along with dimension data in Table 1 were used to compute the dimensional time-period (B) and maximum force loading rates (C) over a range of shear rates for cases 1–8. As an example of how to read these charts, from B we see that at a shear rate of 100/s PMN-homotypic aggregates (Number 1) rotate with a period of 159 ms. In B, time-periods are comparable for all objects except vWF-like molecules. Maximum force loading rate (C) is normal in nature for 1–4, 8 (most cell aggregates and soluble molecules), and shear for 5–7 (cell-surface receptors and highly asymmetric heterotypic aggregates). Parameters correspond to typical cases in Table 1 with media viscosity of 1 cP. 1, PMN doublet; 2, platelet doublet; 3, PMN-platelet; 4, PMN-tumor cell; 5, platelet-tumor cell; 6, platelet receptor; 7, PMN receptor; and 8, vWF-like molecule.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Adler, P. M. 1981. Interaction of unequal spheres. I. Hydrodynamic interaction: colloidal forces. J. Coll. Interf. Sci. 84:461–474.
    1. Alon, R., D. A. Hammer, and T. A. Springer. 1995. Lifetime of the P-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 374:539–542. - PubMed
    1. Arp, P. A., and S. G. Mason. 1977. The kinetics of flowing dispersions. VIII. Doublets of rigid spheres (theoretical). J. Coll. Interf. Sci. 61:21–43.
    1. Ballard, M. C. 1987. Atlas of Blood Cells in Health and Disease. United States Department of Health and Human Services, Atlanta, GA.
    1. Batchelor, G. K. 1967. An Introduction to Fluid Dynamics. Cambridge University Press, Cambridge.

Publication types

Substances

LinkOut - more resources