Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Comparative Study
. 2003;4(11):R76.
doi: 10.1186/gb-2003-4-11-r76. Epub 2003 Oct 24.

Application of independent component analysis to microarrays

Su-In Lee  1 , Serafim Batzoglou
Affiliations
Comparative Study

Application of independent component analysis to microarrays

Su-In Lee et al. Genome Biol. 2003.

Abstract

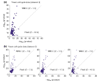
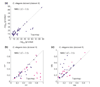
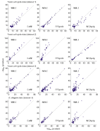
We apply linear and nonlinear independent component analysis (ICA) to project microarray data into statistically independent components that correspond to putative biological processes, and to cluster genes according to over- or under-expression in each component. We test the statistical significance of enrichment of gene annotations within clusters. ICA outperforms other leading methods, such as principal component analysis, k-means clustering and the Plaid model, in constructing functionally coherent clusters on microarray datasets from Saccharomyces cerevisiae, Caenorhabditis elegans and human.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Model of gene expression within a cell. Each genomic expression pattern at a given condition, denoted by xi, is modeled as linear combination of genomic expression programs of independent biological processes. The level of activity of each biological process is different in each environmental condition. The mixing matrix A contains the linear coefficients aij, where aij = activity level of process j in condition i. The example shown uses data generated by Gasch et al. [48].
Figure 2
Figure 2
Comparison of linear ICA (NMLE), nonlinear ICA with Gaussian RBF kernel (NICAgauss), and PCA, on the yeast cell cycle spotted array data (dataset 1). For each functional category within GO and KEGG, the value of -log10 (p value) with the smallest p value from one method is plotted against the corresponding value from the other method. (a) Gene clusters based on the linear ICA components are compared with those based on PCA when C for PCA is fixed to its optimal value 37.5. (b) Gene clusters based on the linear ICA components are compared with those based on PCA with different values of C. (c) Gene clusters based on the nonlinear ICA components are compared with those based on linear ICA. (d) Gene clusters based on the nonlinear ICA components are compared with those based on PCA. Overall, nonlinear ICA performed slightly better than NMLE, and both methods performed significantly better than PCA.
Figure 3
Figure 3
Three independent components of the human normal tissue data (dataset 5). Each gene is mapped to a point based on the value assigned to the gene in the 14th (x-axis), 15th (y-axis) and 55th (z-axis) independent components, which are enriched with liver-specific (red), muscle-specific (orange), and vulva-specific (green) genes, respectively. Genes not annotated as liver-, muscle- or vulva-specific are colored yellow.
Figure 4
Figure 4
Comparison of linear ICA (NMLE), nonlinear ICA with Gaussian RBF kernel (NICAgauss), and k-means clustering on the yeast cell cycle oligonucleotide array data (dataset 2). For each GO and KEGG functional category, the largest -log10(p value) within clusters from one method is plotted against the corresponding value from the other method. (a) Gene clusters based on the linear ICA components are compared with those based on k-means clustering. (b) TP (True Positives) of gene clusters based on the linear ICA components are compared with those of gene clusters based on k-means clustering. Functional categories for which clusters from NMLE have larger p values than those from k-means clustering algorithm are colored in purple. (c) SN (Sensitivity) of gene clusters based on the linear ICA components are compared with gene clusters based on k-means clustering. Functional categories corresponding to the ones in purple in Figure 4b are colored in purple. (d) Gene clusters based on the nonlinear ICA components are compared with those based on linear ICA. (e) Gene clusters based on the nonlinear ICA components are compared with those based on k-means clustering. Overall, nonlinear ICA performed better than NMLE and both methods performed better than k-means clustering.
Figure 5
Figure 5
Comparison of linear ICA (NMLE) with the Plaid models, on the yeast stress spotted array dataset (dataset 3). For each GO and KEGG functional category, the largest -log10(p value) within clusters from one method is plotted against the corresponding value from the other method. (a) Gene clusters based on the NMLE components are compared with those based on the Plaid model when C for the Plaid model is fixed to its optimal value 32.5. (b) Gene clusters based on the linear ICA components are compared with those based on the Plaid model with different values of C.
Figure 6
Figure 6
Comparison of linear ICA (NMLE) versus topomap-based clustering on the C. elegans spotted array dataset (dataset 4). For each functional category within GO and KEGG, the value of -log10 (p value) with the smallest p value from NMLE is plotted against the corresponding value from the topomap method. (a) Gene clusters based on the NMLE components are compared with those based on the Topomap method. The two methods performed comparably, as most points of low p values fall on the x = y axis. (b) TP (True Positives) of functional categories from gene clusters based on the NMLE components are compared with those of functional categories from gene clusters based on the topomap method. Functional categories for which clusters from NMLE have larger p values than those from topomap method are colored in purple. (c) SN (Sensitivity) of functional categories from gene clusters based on the linear NMLE and topomap clusters. Functional categories corresponding to the ones in purple in Figure 6b are colored in purple.
Figure 7
Figure 7
Comparison of NMLE with other ICA approaches. Comparison of the NMLE ICA algorithm with three other ICA approaches on two yeast cell cycle data (dataset 1 and 2), yeast stress data (dataset 3), and C. elegans data (dataset 4). Eight different ICA algorithms and variations (Table 4) were compared. The full comparison is shown in the web supplement. Overall, NMLE, ExtIM and FPsymth performed similarly except in the dataset 2. NICApoly performed comparably with NICAgauss. Both nonlinear approaches were better than NMLE in the two smaller datasets, but performed relatively poorly in the two larger datasets.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Butte A. The use and analysis of microarray data. Nat Rev Drug Discov. 2002;1:951–960. - PubMed
    1. Ando T, Suguro M, Hanai T, Kobayashi T, Honda H, Seto M. Fuzzy neural network applied to gene expression profiling for predicting the prognosis of diffuse large B-cell lymphoma. Jpn J Cancer Res. 2002;93:1207–1212. - PMC - PubMed
    1. Brown M, Grundy WN, Lin D, Cristianini N, Sugnet CW, Furey TS, Ares M, Haussler D. Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc Natl Acad Sci USA. 2000;97:262–267. - PMC - PubMed
    1. Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. - PubMed
    1. Mukherjee S, Tamayo P, Mesirov JP, Slonim D, Verri A, Poggio T. Technical Report No 182, AI Memo 1676. MIT, Cambridge: Massachusetts Institute of Technology; 1999. Support vector machine classification of microarray data.

Publication types

MeSH terms

LinkOut - more resources