Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 1999 Nov 1;19(21):9587-603.
doi: 10.1523/JNEUROSCI.19-21-09587.1999.

Synaptic basis of cortical persistent activity: the importance of NMDA receptors to working memory

X J Wang  1
Affiliations

Synaptic basis of cortical persistent activity: the importance of NMDA receptors to working memory

X J Wang. J Neurosci. .

Abstract

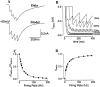
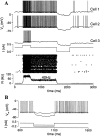
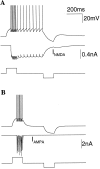
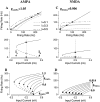
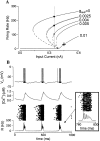
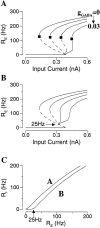
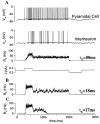
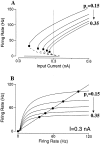
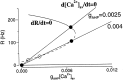
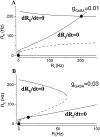
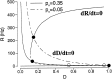
Delay-period activity of prefrontal cortical cells, the neural hallmark of working memory, is generally assumed to be sustained by reverberating synaptic excitation in the prefrontal cortical circuit. Previous model studies of working memory emphasized the high efficacy of recurrent synapses, but did not investigate the role of temporal synaptic dynamics. In this theoretical work, I show that biophysical properties of cortical synaptic transmission are important to the generation and stabilization of a network persistent state. This is especially the case when negative feedback mechanisms (such as spike-frequency adaptation, feedback shunting inhibition, and short-term depression of recurrent excitatory synapses) are included so that the neural firing rates are controlled within a physiological range (10-50 Hz), in spite of the exuberant recurrent excitation. Moreover, it is found that, to achieve a stable persistent state, recurrent excitatory synapses must be dominated by a slow component. If neuronal firings are asynchronous, the synaptic decay time constant needs to be comparable to that of the negative feedback; whereas in the case of partially synchronous dynamics, it needs to be comparable to a typical interspike interval (or oscillation period). Slow synaptic current kinetics also leads to the saturation of synaptic drive at high firing frequencies that contributes to rate control in a persistent state. For these reasons the slow NMDA receptor-mediated synaptic transmission is likely required for sustaining persistent network activity at low firing rates. This result suggests a critical role of the NMDA receptor channels in normal working memory function of the prefrontal cortex.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
Temporal summation of the NMDAR-mediated EPSCs.A, NMDAR-mediated EPSCs elicited by four stimuli, when the membrane potential is clamped at −40 mV. Top panel, Data from a pyramidal neuron in CA1 of the rat hippocampus (redrawn fromHestrin et al., 1990b, with permission). The stimulus is at 25 Hz. Note the significant summation and saturation. These properties are mediated postsynaptically by the NMDARs, because they are absent in the non-NMDR-mediated EPSCs recorded in the same cell at −100 mV.Bottom panel, NMDAR-mediated EPSCs produced by the model synapse (Eqs. 4, 5); the stimulus is at 20 Hz. gNMDA = 0.07; αx = 1, τx = 2 msec; αs = 0.3, τs = 120 msec. B, NMDAR-mediated EPSCs of the model synapse at various stimulus frequencies R. The EPSC amplitude decreases in time in each train, and its steady state is smaller at higher R. The average current saturates at high R. C, The ratio of the NMDAR-mediated EPSC in the steady state (ΔINMDA, ss) over its initial value (ΔINMDA,0), as function of the stimulus frequency. Solid curve, A(R) = 1/(1 + 0.025 ∗ R)2, which fits well the simulation data; therefore ΔINMDA,ss ∼ 1/R2 at high R. D, The average sNMDA as function of stimulus frequency.Solid curve, sNMDA = νR/(νR + 1), ν = αxαsτxτs.
Fig. 2.
Fig. 2.
Persistent active state in an excitatory neural network. A, Panels from top to bottom, membrane potentials of three cells, external input current, rastergram, and population firing rate. The network model is initially at rest. In response to a transient current pulse, the network is activated. After the termination of the input, neurons continue to discharge spikes asynchronously with an average firing rate of 40 Hz [R(t) is constant in time; see also the rastergram]. In this simulation, there is a Gaussian distribution of the leak conductance gL across the cell population, with a mean of 0.025 μS and SD of 0.003 μS. Cells with the least gL display spontaneous firing in the rest state (Cells 1, 2), whereas cells with the largest gL do not show sustained firing in the network persistent state (Cell 3) (gAMPA = 0.2; gNMDA = 0.04; I = 0.3 nA).B, Bistability is a network phenomenon. During persistent activity, a neuron is hyperpolarized by a current pulse (with two different intensities) to a negative membrane potential, but at the end of the perturbation the firing activity resumes itself because of the massive synaptic drive from the network.
Fig. 3.
Fig. 3.
Tonic synaptic drive is required to sustain a persistent active state. A, A single neuron with an autapse of the NMDA type is excited from the rest to an active state that outlasts the transient input. The persistent firing is at 36 Hz. Note the tonic NMDAR-mediated current (gNMDA = 0.1). B, If the synaptic current is mediated by the AMPARs (gAMPA = 1.5), the synaptic current fluctuates rapidly between a maximum and zero. When it is zero, the cell does not receive synaptic drive any more; therefore the cell decays back to the rest state as soon as the input is withdrawn. Note the different scale for the synaptic current in A andB.
Fig. 4.
Fig. 4.
Slow NMDAR channels can sustain a persistent active state in which the network dynamics is partially synchronous. The network model consists of two (pyramid and interneuron) populations. The network is initially at rest and is switched to the active state by a transient input. Synchronous oscillations at 8 Hz are generated by the interplay between the fast recurrent AMPAR-activated excitation and slower feedback inhibition. Note that the pyramidal cell and interneuron populations show very small relative phase shift (inset). The AMPAR-activated synaptic drive sAMPA phasically oscillates between zero and a maximum, whereas the NMDAR-activated synaptic drive sNMDA remains at a significantly high level, which is sufficient to maintain the network activity (gAMPA,ee = 0.7; gNMDA,ee = 0.07; gAMPA,ei = 0.2; gNMDA,ei = 0.02; gGABA = 0.1; I = 0.3 nA).
Fig. 5.
Fig. 5.
Frequency–current relation for a bistable network of pyramidal neurons. A, Bistability with AMPAR-activated synaptic drive (gAMPA = 1.05). Top panel, For a fixed external input drive, the population firing rate of the asynchronous state is given by R = f(R). Such states are obtained graphically by the intersections of the function f(R) with the diagonal line. There are three states for I = 0.3 (solid curve); two (rest and active) states are stable (filled circles), and one is unstable (open circle). If I is too small (I = 0.1;dotted line) or too large (I = 0.5;dash-dotted line), there is only one steady state that is resting or active, respectively. Bottom panel, Bistability is manifested by the presence of three branches of the frequency–current curve; the bottom branch is the rest state, the top branch is the active state, and the middle branch is unstable. Within a range of external input current, denoted by Ia and Ib, the network can be either at rest or in the active state. B, Different frequency–current curves correspond to gAMPA = 0.6 to 1.5, by increment of 0.15. With larger gAMPA the bistable range (Ib − Ia) is wider, but the lowest firing rate of the active state located at Ia (filled square) is dramatically increased. C, Bistability with NMDAR-activated synaptic drive (gNMDA = 0.006). Top panel, For a fixed I = 0.3 nA, with NMDAR channels the function f(R) shows a plateau at relatively low R values, because of the saturation of the NMDAR-activated conductance (compare Fig. 1), yielding a relatively low firing rate of the persistent state. Bottom panel, Frequency–current curve. D, Different frequency–current curves correspond to gNMDA = 0.0 to 0.014 by increment of 0.002 (the asynchronous state was calculated with [Mg2+] = 0). With larger gNMDA the bistable range is wider (Ia is shifted to the left), whereas the minimal firing rate of the persistent state (filled square) remains <40 Hz.
Fig. 6.
Fig. 6.
Effect of spike-frequency adaptation in an excitatory network (gAMPA = 1.2).A, Frequency–current curves with different gAHP values. For a given input current (e.g., I = 0.35 nA; vertical dotted line), the firing rate is decreased by increasing gAHP. At the same time, the bistable range shrinks, and the bistability disappears when gAHP is >0.005. Dotted line, gAMPA = 0.99 and gAHP = 0, which is superimposable with that of gAMPA = 1.2 and gAHP = 0.0025. The persistent state at reduced firing rate (e.g. open circle at I = 0.35 and gAHP = 0.004) is unstable if the excitatory synapses are mediated by the fast AMPARs (see ).B, Adaptation induced network rhythmic bursting. When the asynchronous state is unstable and does not coexist with the rest state, the network displays synchronous burst firing patterns (with I = 0.45 and gAHP = 0.01, indicated by a cross in A). Strong and fast recurrent excitation recruits neurons and accelerates neural discharges, until IAHP grows sufficiently to terminate the burst. IAHP then decays back to zero, and the cycle starts over again. Note that the neural firing is coherent at the onset of the burst, but desynchronizes within the burst (inset).
Fig. 7.
Fig. 7.
Effect of feedback shunting inhibition.A, B, Frequency–current curves with different gGABA values when isolated interneurons are near or well below the firing threshold, respectively (C).A, Stronger gGABA reduces the bistable range and abolishes the persistent state. Note that the lowest firing rate of persistent activity (filled square) is hardly changed by inhibition. B, In this case, the portion of the frequency–current curve with RE < 25 Hz is unaffected by recurrent inhibition. With sufficiently large gGABA, bistability is preserved, and the active states have reasonably low firing rates (25–50 Hz).C, The firing rate RI of interneurons as function of RE for A andB (gAMPA,ee = 1.2, gAMPA,ei = 0.4; the Poisson input rate to interneurons is λ = 2500 Hz in A and 2000 Hz inB).
Fig. 8.
Fig. 8.
The low rate asynchronous state is not stable if excitatory synapses are too fast. The network model is simulated in the presence of strong recurrent inhibition. The speed of the excitatory synaptic kinetics is varied, whereas the steady–state synaptic drive and the mean firing rate are preserved. A, With τE = 80 msec, the network can be turned on to the persistent state with RE ≃ 33 Hz. Note the slow ramping-up of RE(t) during the transient stimulus, caused by the temporal summation of the slow synaptic current. B, With τE = 18 msec, the persistent state is still stable, but RE(t) displays large fluctuations in time.C, With τE = 17 msec, the fluctuations eventually bring RE(t) too close to zero, and the network returns to the rest state (same parameters as in Fig. 7B, with gGABA = 0.03 and I = 0.34 nA).
Fig. 9.
Fig. 9.
Rate control by short-term synaptic depression (STD). A, Without STD the firing rate of the persistent state is typically high, as long as there is a substantial AMPAR-mediated component of the recurrent synaptic transmission.B, The addition of STD (pυ = 0.3) significantly reduced the firing rate to ∼40 Hz, within the physiological range of PFC cells. Note that during the transient depolarizing pulse R(t) has a rapid peak, then decreases to a low steady state caused by STD (see D(t)). There is a trough in R(t) immediately after the input pulse, when D(t) recovers and reaches a steady state (gAMPA = 0.7; gNMDA = 0.07; I = 0.3 nA).
Fig. 10.
Fig. 10.
Effect of short-term synaptic depression in an excitatory neural network. A, Frequency–current curves with pυ = 0.15 to 0.35, by increment of 0.05. Short-term depression reduces the lowest firing rates of the active states (filled square), whereas the bistable range remains reasonably large. B, For a fixed input current (I = 0.3 nA) in A, the firing rate of the asynchronous state is given by R = f(R); or the intersections of f(R) with the diagonal line. Stronger short-term depression leads to saturation of the function f(R) at progressively lower firing rates, so that rate control is achieved for the persistent state. (gAMPA = 8).
Fig. 11.
Fig. 11.
Stability of the persistent state in a sparse network with short-term depression (average number of synapses per neuron Msyn = 100 except for B).A, For each of the five active states in Figure10B, the network model is simulated, whereas the synaptic time constant τE is varied systematically. The minimal value of τE for which the persistent state was observed is plotted against the firing rate. Thus, the lower is the firing rate, the slower the synapses must be to sustain the network persistent activity. B, The required minimal τE is not sensitive to Msyn, as long as the latter is >100.C, D, An example with pυ = 0.35 and R = 35 Hz. The initial condition for the network simulation was prescribed to be as close to the asynchronous state as possible. C, For τE = 49 msec, the fluctuations of the network activity as measured by R(t) grow in time, and eventually die out. Bottom panel, Histogram of the number of connections per neuron, centered at Msyn = 100. C, For τE = 50 msec, network fluctuations are damped out, and the persistent state is stabilized. Bottom panel, The neural firing rate is a linear function of the number of synaptic inputs and varies in a wide range (20–60 Hz) across the population.
Fig. 12.
Fig. 12.
Phase-plane analysis for spike-frequency adaptation. The R -nullcline plotted as function of gAHP [Ca2+] is independent of gAHP. The [Ca2+] -nullcline is given by Equation20. It is a straight line, with a decreasing slope for larger gAHP. The steady states are given by the intersections of the two nullclines. The persistent state is located at the top branch of the R -nullcline with small gAHP, and is moved to the middle branch with large gAHP. This active state on the middle branch is not stable if the excitatory synaptic decay is much faster than the adaptation time constant. Same parameters as in Figure6A (I = 0.35 nA).
Fig. 13.
Fig. 13.
Phase-plane analysis for recurrent shunting inhibition. A, For small gGABA, the active state is located on the top branch of the RE-nullcline. B, For large gGABA, it is shifted to the middle branch of the RE-nullcline with a low firing rate. This active state on the middle branch is not stable if the excitatory synapse is fast compared to the inhibitory synapse. Same parameters as in Figure 7B (I = 0.34 nA).
Fig. 14.
Fig. 14.
Phase-plane analysis for short-term synaptic depression. The R -nullcline is independent of the depression parameter pυ, and the D -nullcline is shown with two pυvalues. For small pυ, the persistent state is located on the top branch of the R -nullcline. For large pυ, it is shifted to the middle branch with reduced firing rate. This active state is not stable if the excitatory synaptic decay is much faster than the effective time constant of synaptic depression. Same parameters as in Figure 10(I = 0.3 nA).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Abbott LF. Realistic synaptic inputs for model neural networks. Network. 1991;2:245–258.
    1. Abbott LF, van Vreeswijk C. Asynchronous states in networks of pulse-coupled oscillators. Phys Rev. 1993;48:1483–1490. - PubMed
    1. Abbott LF, Varela JA, Sen K, Nelson SB. Synaptic depression and cortical gain control. Science. 1997;275:220–224. - PubMed
    1. Akbarian S, Sucher NJ, Bradley D, Tafazzoli A, Trinh D, Hetrick WP, Potkin SG, Sandman CA, Bunney WE, Jr, Jones EG. Selective alterations in gene expression for NMDA receptor subunits in prefrontal cortex of schizophrenics. J Neurosci. 1996;16:19–30. - PMC - PubMed
    1. Amari S. Dynamics of pattern formation in lateral-inhibition type neural fields. Biol Cybern. 1977;27:77–87. - PubMed

Publication types

Substances