Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Dec 2;4(1):vbae193.
doi: 10.1093/bioadv/vbae193. eCollection 2024.

Optimizing design of genomics studies for clonal evolution analysis

Arjun Srivatsa  1 , Russell Schwartz  1   2
Affiliations

Optimizing design of genomics studies for clonal evolution analysis

Arjun Srivatsa et al. Bioinform Adv. .

Abstract

Motivation: Genomic biotechnology has rapidly advanced, allowing for the inference and modification of genetic and epigenetic information at the single-cell level. While these tools hold enormous potential for basic and clinical research, they also raise difficult issues of how to design studies to deploy them most effectively. In designing a genomic study, a modern researcher might combine many sequencing modalities and sampling protocols, each with different utility, costs, and other tradeoffs. This is especially relevant for studies of somatic variation, which may involve highly heterogeneous cell populations whose differences can be probed via an extensive set of biotechnological tools. Efficiently deploying genomic technologies in this space will require principled ways to create study designs that recover desired genomic information while minimizing various measures of cost.

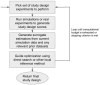
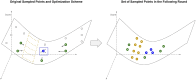
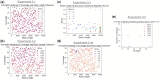
Results: The central problem this paper attempts to address is how one might create an optimal study design for a genomic analysis, with particular focus on studies involving somatic variation that occur most often with application to cancer genomics. We pose the study design problem as a stochastic constrained nonlinear optimization problem. We introduce a Bayesian optimization framework that iteratively optimizes for an objective function using surrogate modeling combined with pattern and gradient search. We demonstrate our procedure on several test cases to derive resource and study design allocations optimized for various goals and criteria, demonstrating its ability to optimize study designs efficiently across diverse scenarios.

Availability and implementation: https://github.com/CMUSchwartzLab/StudyDesignOptimization.

PubMed Disclaimer

Conflict of interest statement

None declared.

Figures

Figure 1.
Figure 1.
A flowchart of the main algorithm is depicted above. The algorithm repeatedly estimates surrogate functions from simulation calls chosen to explore regions of the search space of uncertain quality while exploiting regions of known high solution quality via focused local search.
Figure 2.
Figure 2.
Illustration of the optimization algorithm on a simplified example. The algorithm starts with a Latin hypercube sample of the input space. New points are explored in three main ways to balance exploitation of known high-quality solutions with exploration of poorly characterized regions of the search space. Points depicted in green are generated via a gradient descent search step with a numerical estimation of the gradient. Points depicted in gold and by the gold mesh in the left image are drawn from regions of high variance in the Gaussian process estimation and explored in the next round via the lower acquisition bound criteria. The minimal point in blue on the left is explored via a mesh search of points in the local neighborhood in the next round.
Figure 3.
Figure 3.
Visualizations from the five experimental queries. (a, b, d) 2D plots of coverage and read length versus score highlighting how different tradeoffs in the study design space by experiment yield different high-scoring regions. (c) Plots read length versus score colored by round of optimization. (e) Plots number of samples and coverage, showing how a higher cost-prioritization favors low coverage high sample points.
See this image and copyright information in PMC

Update of

Similar articles

See all similar articles

References

    1. Abramson MA. Pattern Search Algorithms for Mixed Variable General Constrained Optimization Problems. Houston, Texas, United States: Rice University, 2003.
    1. Alexandrov LB, Kim J, Haradhvala NJ. et al.; PCAWG Consortium. The repertoire of mutational signatures in human cancer. Nature 2020;578:94–101. - PMC - PubMed
    1. Audet C, Dennis JE Jr. Pattern search algorithms for mixed variable programming. SIAM J Optim 2001;11:573–94.
    1. Barbari SR, Shcherbakova PV.. Replicative DNA polymerase defects in human cancers: consequences, mechanisms, and implications for therapy. DNA Repair (Amst) 2017;56:16–25. - PMC - PubMed
    1. Das SK, Menezes ME, Bhatia S. et al. Gene therapies for cancer: strategies, challenges and successes. J Cell Physiol 2015;230:259–71. - PMC - PubMed

LinkOut - more resources