Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Jun 20;14(6):620.
doi: 10.3390/brainsci14060620.

A Computational Model of Deep Brain Stimulation for Parkinson's Disease Tremor and Bradykinesia

Sandeep Sathyanandan Nair  1 , Srinivasa Chakravarthy  1   2
Affiliations

A Computational Model of Deep Brain Stimulation for Parkinson's Disease Tremor and Bradykinesia

Sandeep Sathyanandan Nair et al. Brain Sci. .

Abstract

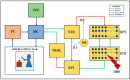
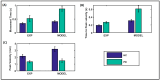
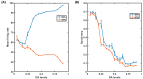
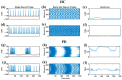
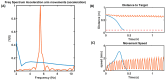
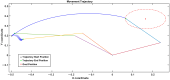
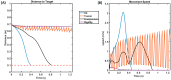
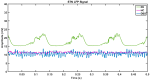
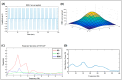
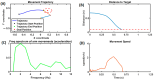
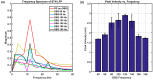
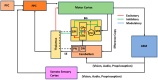
Parkinson's disease (PD) is a progressive neurological disorder that is typically characterized by a range of motor dysfunctions, and its impact extends beyond physical abnormalities into emotional well-being and cognitive symptoms. The loss of dopaminergic neurons in the substantia nigra pars compacta (SNc) leads to an array of dysfunctions in the functioning of the basal ganglia (BG) circuitry that manifests into PD. While active research is being carried out to find the root cause of SNc cell death, various therapeutic techniques are used to manage the symptoms of PD. The most common approach in managing the symptoms is replenishing the lost dopamine in the form of taking dopaminergic medications such as levodopa, despite its long-term complications. Another commonly used intervention for PD is deep brain stimulation (DBS). DBS is most commonly used when levodopa medication efficacy is reduced, and, in combination with levodopa medication, it helps reduce the required dosage of medication, prolonging the therapeutic effect. DBS is also a first choice option when motor complications such as dyskinesia emerge as a side effect of medication. Several studies have also reported that though DBS is found to be effective in suppressing severe motor symptoms such as tremors and rigidity, it has an adverse effect on cognitive capabilities. Henceforth, it is important to understand the exact mechanism of DBS in alleviating motor symptoms. A computational model of DBS stimulation for motor symptoms will offer great insights into understanding the mechanisms underlying DBS, and, along this line, in our current study, we modeled a cortico-basal ganglia circuitry of arm reaching, where we simulated healthy control (HC) and PD symptoms as well as the DBS effect on PD tremor and bradykinesia. Our modeling results reveal that PD tremors are more correlated with the theta band, while bradykinesia is more correlated with the beta band of the frequency spectrum of the local field potential (LFP) of the subthalamic nucleus (STN) neurons. With a DBS current of 220 pA, 130 Hz, and a 100 microsecond pulse-width, we could found the maximum therapeutic effect for the pathological dynamics simulated using our model using a set of parameter values. However, the exact DBS characteristics vary from patient to patient, and this can be further studied by exploring the model parameter space. This model can be extended to study different DBS targets and accommodate cognitive dynamics in the future to study the impact of DBS on cognitive symptoms and thereby optimize the parameters to produce optimal performance effects across modalities. Combining DBS with rehabilitation is another frontier where DBS can reduce symptoms such as tremors and rigidity, enabling patients to participate in their therapy. With DBS providing instant relief to patients, a combination of DBS and rehabilitation can enhance neural plasticity. One of the key motivations behind combining DBS with rehabilitation is to expect comparable results in motor performance even with milder DBS currents.

Keywords: Parkinson’s disease; basal ganglia; beta; bradykinesia; deep brain stimulation (DBS); dopamine; motor symptoms; rigidity; sub thalamic nucleus; theta; tremor.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Block diagram of the proposed cortico-basal ganglia model. The model consists of a 2-link arm model, the proprioceptive cortex (PC), the prefrontal cortex (PFC), the motor cortex (MC), and the basal ganglia (BG). Here, the input nucleus striatum, the output nucleus globus pallidus internus (GPi), the globus pallidus externus (GPe), the subthalamic nucleus (STN), and the thalamus (THAL) constitute the BG. MC integrates the inputs received from the prefrontal cortex (PFC) and the proprioceptive cortex (PC) along with the feedback signal from BG and sends the signal to the arm via the spinal motor neurons.
Figure 2
Figure 2
Comparison of performance of the proposed model with experimental data adapted from [61]. (A) Movement time, (B) time-to-peak velocity, (C) peak velocity; sec, second; m/s, meter per second. The dark blue bar represents the healthy control (HC) group, and the green bar represents the PD condition.
Figure 3
Figure 3
Firing rates and synchrony. (A) The firing rates of STN and GPe neurons for various values of DA levels are shown. The blue line represents the GPe, and the orange line represents the STN neurons. (B) Synchrony within STN and GPe nuclei. Again, blue and orange lines represent the GPe and STN neurons, respectively. Synchrony keeps decreasing with increasing DA levels. The mean and variance values for the above plots were calculated over five epochs.
Figure 4
Figure 4
The firing of single STN and GPe neurons in the HC group is shown in (a,d). Under HC conditions, both the STN and GPe neurons exhibit regular firings. The firing of single STN and GPe neurons under PD conditions is shown in (g,j). (b,e) The raster plot of the STN, and (h,k) the GPe neurons in PD. (c,f) the synchrony of STN and GPe neurons under healthy conditions, and (i,l) the synchrony of STN and GPe neurons under PD condition. The orange lines in (a,d,g,j) indicate the reference line corresponding to the theoretical resting membrane potential (-60 mV) and the blue line represents the spike data.
Figure 5
Figure 5
(A) The frequency spectrum of the acceleration of the arm movements. The blue line represents the healthy control (HC) condition, and the orange line represents the PD tremor condition in all (A–C). (B) This plot shows the distance to the target as the time progresses. (C) The velocity of the arm movement, where the curve follows a bell curve under HC conditions and keeps oscillating under PD tremor conditions.
Figure 6
Figure 6
The trajectory of the arm movements is given. The blue line (for the arm) represents the healthy control (HC) condition, the yellow line (for the arm) represents the tremor condition, and the green line (for the arm) represents the rigidity condition. In the case of HCs, the reaching is successful, whereas in the case of tremor and rigidity, it is not.
Figure 7
Figure 7
(A) This plot shows the distance to the target as the time progresses. (B) This plot shows the velocity of the arm movement, where the curve follows a bell curve for the HCs, has multiple lesser-magnitude peaks under the bradykinesia condition, and keeps oscillating under the PD tremor condition. The arm hardly moves, and the velocity curve quickly decreases down under rigidity conditions. The blue line represents the healthy controls (HCs), the purple line represents the rigidity condition, the orange line represents the tremor condition, and the black line represents the bradykinesia condition.
Figure 8
Figure 8
The potential of the STN neuronal population in the local field is shown. The violet curve indicates the HC condition, the green line indicates the PD condition, and the blue line represents the DBS-treated condition.
Figure 9
Figure 9
(A) DBS is currently applied to the center of most neurons in the STN population. (B) The spread of the current in nearby neurons. (C) The FFT of the local field potential of the STN population. (D) The mean relative power of the LFP of the STN was redrawn as recorded in the experimental studies (Kuhn et al., 2008) [68].
Figure 10
Figure 10
The movement trajectory of the arm movements is given in (A), where the blue line represents the trajectory and the red dot represents the target position. The distance to target over time is shown in (B), where as the frequency spectrum of the acceleration of arm movements is shown in (C) and the velocity of arm movements is shown in (D).
Figure 11
Figure 11
(A) The frequency spectra of STN LFP for PD and DBS-applied conditions are shown. (B) The peak velocities during a reaching task for varying DBS frequencies are shown.
Figure 12
Figure 12
Hypothetical block diagram with the integrated cortico-basal ganglia and the corticocerebellar loops. PPC, posterior parietal cortex; STR, striatum; PN, pontine nuclei, DN, dentate nuclei; PFC, prefrontal cortex; GPe/GPi globus pallidus externus and globus pallidus interna.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Muddapu V.R., Chakravarthy V.S. Influence of energy deficiency on the subcellular processes of substantia nigra pars compacta cell for understanding Parkinsonian neurodegeneration. Sci. Rep. 2021;11:1754. doi: 10.1038/s41598-021-81185-9. - DOI - PMC - PubMed
    1. Gonzalez-Rodriguez P., Zampese E., Surmeier D.J. Progress in Brain Research. Volume 252. Elsevier B.V.; Amsterdam, The Netherlands: 2020. Selective neuronal vulnerability in Parkinson’s disease; pp. 61–89. - DOI - PubMed
    1. Marino B.L., de Souza L.R., Sousa K.P., Ferreira J.V., Padilha E.C., da Silva C.H., Taft C.A., Hage-Melim L.I. Parkinson’s Disease: A review from pathophysiology to treatment. Mini-Rev. Med. Chem. 2020;20:754–767. doi: 10.2174/1389557519666191104110908. - DOI - PubMed
    1. Morley J.F., Duda J.E. Olfaction as a biomarker in Parkinson’s disease. Biomarkers Med. 2010;4:661–670. doi: 10.2217/bmm.10.95. - DOI - PubMed
    1. Fullard M.E., Morley J.F., Duda J.E. Olfactory dysfunction as an early biomarker in Parkinson’s disease. Neurosci. Bull. 2017;33:515–525. doi: 10.1007/s12264-017-0170-x. - DOI - PMC - PubMed

Grants and funding

This research was funded by the Parkinson’s Therapeutics Laboratory, which is supported by the 1972 Reunion batch of IIT Madras grant number [CR23241346BTDONO005028] and the APC has been completely waivered.

LinkOut - more resources