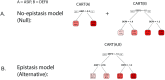
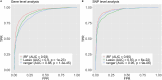
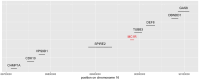
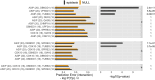
Detecting epistatic drivers of human phenotypes is a considerable challenge. Traditional approaches use regression to sequentially test multiplicative interaction terms involving pairs of genetic variants. For higher-order interactions and genome-wide large-scale data, this strategy is computationally intractable. Moreover, multiplicative terms used in regression modeling may not capture the form of biological interactions. Building on the Predictability, Computability, Stability (PCS) framework, we introduce the epiTree pipeline to extract higher-order interactions from genomic data using tree-based models. The epiTree pipeline first selects a set of variants derived from tissue-specific estimates of gene expression. Next, it uses iterative random forests (iRF) to search training data for candidate Boolean interactions (pairwise and higher-order). We derive significance tests for interactions, based on a stabilized likelihood ratio test, by simulating Boolean tree-structured null (no epistasis) and alternative (epistasis) distributions on hold-out test data. Finally, our pipeline computes PCS epistasis p-values that probabilisticly quantify improvement in prediction accuracy via bootstrap sampling on the test set. We validate the epiTree pipeline in two case studies using data from the UK Biobank: predicting red hair and multiple sclerosis (MS). In the case of predicting red hair, epiTree recovers known epistatic interactions surrounding MC1R and novel interactions, representing non-linearities not captured by logistic regression models. In the case of predicting MS, a more complex phenotype than red hair, epiTree rankings prioritize novel interactions surrounding HLA-DRB1, a variant previously associated with MS in several populations. Taken together, these results highlight the potential for epiTree rankings to help reduce the design space for follow up experiments.