Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Jan 20;4(1):100143.
doi: 10.1016/j.bpr.2024.100143. eCollection 2024 Mar 13.

Quantifying the minimum localization uncertainty of image scanning localization microscopy

Dylan Kalisvaart  1 , Shih-Te Hung  1 , Carlas S Smith  1   2
Affiliations

Quantifying the minimum localization uncertainty of image scanning localization microscopy

Dylan Kalisvaart et al. Biophys Rep (N Y). .

Abstract

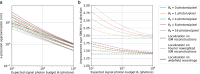
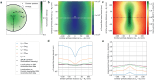
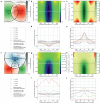
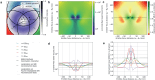
Modulation enhanced single-molecule localization microscopy (meSMLM), where emitters are sparsely activated with sequentially applied patterned illumination, increases the localization precision over single-molecule localization microscopy (SMLM). The precision improvement of modulation enhanced SMLM is derived from retrieving the position of an emitter relative to individual illumination patterns, which adds to existing point spread function information from SMLM. Here, we introduce SpinFlux: modulation enhanced localization for spinning disk confocal microscopy. SpinFlux uses a spinning disk with pinholes in its illumination and emission paths, to sequentially illuminate regions in the sample during each measurement. The resulting intensity-modulated emission signal is analyzed for each individual pattern to localize emitters with improved precision. We derive a statistical image formation model for SpinFlux and we quantify the theoretical minimum localization uncertainty in terms of the Cramér-Rao lower bound. Using the theoretical minimum uncertainty, we compare SpinFlux to localization on Fourier reweighted image scanning microscopy reconstructions. We find that localization on image scanning microscopy reconstructions with Fourier reweighting ideally results in a global precision improvement of 2.1 over SMLM. When SpinFlux is used for sequential illumination with three patterns around the emitter position, the localization precision improvement over SMLM is twofold when patterns are focused around the emitter position. If four donut-shaped illumination patterns are used for SpinFlux, the maximum local precision improvement over SMLM is increased to 3.5. Localization of image scanning microscopy reconstructions thus has the largest potential for global improvements of the localization precision, where SpinFlux is the method of choice for local refinements.

PubMed Disclaimer

Conflict of interest statement

The authors have no conflicts to disclose.

Figures

Figure 1
Figure 1
Schematic overview of SpinFlux image formation and analysis. (a) In SpinFlux, a rotating disk containing pinholes is placed in the illumination and emission paths. This causes patterned illumination (green cadre) in the sample, modulating the emission intensity of emitters in the sample based on their relative distance to the pattern. Subsequently, the emission signal (orange cadre) is windowed by the pinhole. Rapidly switching the laser on and off causes stroboscopic illumination of emitters in the sample with stationary illumination patterns. (b) SpinFlux obtains its localization precision improvement by merging localized emitter data with information about the relative distance between an illumination pattern and the emitter, derived from photon counts. In this way, it improves the localization precision over SMLM, which only uses localized emitter data and ignores pattern information. We compare SpinFlux with an idealized approach, in which first an ISM acquisition and reconstruction are performed. Afterward, isolated emitters are localized in the ISM reconstruction. (c) Schematic overview of SpinFlux localization variants. In the main text, we consider SpinFlux with one, two, three, and four sequentially applied illumination patterns. The configurations with one, two, and three patterns use Gaussian beams, the configuration with four patterns uses donut beams. Additional configurations are explored in the supporting document.
Figure 2
Figure 2
Approximation of the theoretical minimum localization uncertainty of SMLM on reconstructions acquired from (Fourier reweighted) ISM. For this simulation, a PSF standard deviation of 93.3 nm and a camera pixel size of 65 nm were used. (a) Approximate CRLB in the x-direction as a function of the expected signal photon budget for varying values of the expected background photon count. (b) Improvement of the approximate CRLB over SMLM as a function of the expected signal photon budget for varying values of the expected background photon count.
Figure 3
Figure 3
Theoretical minimum localization uncertainty of SpinFlux localization with one x-offset pinhole and pattern. For this simulation, 2000 expected signal photons and 8 expected background photons per pixel were used. Results are evaluated for the scenario where the entire signal photon budget is exhausted after illumination with the pattern (disregarding signal photons blocked by the spinning disk). (a) Schematic overview of SpinFlux localization with one pinhole with radius rp centered at coordinates (xp,yp). In (d) and (e), the x-distance (xp−θx) between the pinhole and the emitter is varied, where yp=θy. (b) SpinFlux CRLB in the x-direction as a function of the emitter-pinhole x- and y-distances for pinhole radius rp=3σPSF. (c) Improvement of the SpinFlux CRLB over SMLM as a function of the emitter-pinhole x- and y-distances, for pinhole radius rp=3σPSF. (d) CRLB in the x-direction as a function of the emitter-pinhole x-distance. Simulations show SpinFlux with varying pinhole sizes, widefield SMLM, and localization on ISM reconstructions. (e) Improvement of the SpinFlux CRLB over SMLM as a function of the emitter-pinhole x-distance for varying pinhole sizes.
Figure 4
Figure 4
Theoretical minimum localization uncertainty of SpinFlux localization with multiple pinholes and patterns. For this simulation, 2000 expected signal photons and 8 expected background photons per pixel were used, with pinhole radius rp=3σPSF. Results are evaluated for the scenario where the entire signal photon budget is exhausted after illumination with all patterns (disregarding signal photons blocked by the spinning disk). (a) Schematic overview of SpinFlux localization with two pinholes, separated in x by distance s and centered around the focus coordinates (xf,yf). In (d) and (e), the x-distance (xf−θx) between the pattern focus and the emitter is varied, where yf=θy. (b) SpinFlux CRLB in the x-direction as a function of the emitter-pinhole x- and y-distances for pinhole separation rp=4σPSF. (c) Improvement of the SpinFlux CRLB over SMLM as a function of the emitter-pinhole x- and y-distances for pinhole separation rp=4σPSF. (d) CRLB in the x-direction as a function of the emitter-focus x-distance. Simulations show SpinFlux with varying pinhole separations, widefield SMLM, and localization on ISM reconstructions. (e) Improvement of the SpinFlux CRLB over SMLM as a function of the emitter-focus x-distance for varying pinhole separations. (f) Schematic overview of SpinFlux localization with a triangle of three pinholes, centered at focus coordinates (xf,yf) at a radius r. In (i) and (j), the x-distance (xf−θx) between the pattern focus and the emitter is varied, where yf=θy. (g) SpinFlux CRLB in the x-direction as a function of the emitter-pinhole x- and y-distances for pinhole spacing r=2σPSF. (h) Improvement of the SpinFlux CRLB over SMLM as a function of the emitter-pinhole x- and y-distances for pinhole spacing r=2σPSF. (i) CRLB in the x-direction as a function of the emitter-focus x-distance. Simulations show SpinFlux with varying pinhole spacing, widefield SMLM, and localization on ISM reconstructions. (j) Improvement of the SpinFlux CRLB over SMLM as a function of the emitter-focus x-distance for varying pinhole spacing.
Figure 5
Figure 5
Theoretical minimum localization uncertainty of SpinFlux localization with four pinholes and donut-shaped patterns in an equilateral triangle configuration with a center pinhole. For this simulation, 2000 expected signal photons and 8 expected background photons per pixel were used, with pinhole radius rp=3σPSF. Results are evaluated for the scenario where the entire signal photon budget is exhausted after illumination with all patterns (disregarding signal photons blocked by the spinning disk). (a) Schematic overview of SpinFlux localization with a triangle of three pinholes with an additional center pinhole centered at focus coordinates (xf,yf). In (d) and (e), the x-distance (xf−θx) between the pattern focus and the emitter is varied, where yf=θy. (b) SpinFlux CRLB in the x-direction as a function of the emitter-pinhole x- and y-distances for pinhole spacing r=3σPSF. (c) Improvement of the SpinFlux CRLB over SMLM as a function of the emitter-pinhole x- and y-distances for pinhole spacing r=3σPSF. (d) CRLB in the x-direction as a function of the emitter-focus x-distance. Simulations show SpinFlux with varying pinhole spacing, widefield SMLM, and localization on ISM reconstructions. (e) Improvement of the SpinFlux CRLB over SMLM as a function of the emitter-focus x-distance for varying pinhole spacing.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Betzig E., Patterson G.H., et al. Hess H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–1645. https://science.sciencemag.org/content/313/5793/1642.full.pdf - PubMed
    1. Rust M.J., Bates M., Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (storm) Nat. Methods. 2006;3:793–795. - PMC - PubMed
    1. Huang B., Bates M., Zhuang X. Super-resolution fluorescence microscopy. Annu. Rev. Biochem. 2009;78:993–1016. - PMC - PubMed
    1. Reymond L., Huser T., et al. Wieser S. Modulation-enhanced localization microscopy. J. Phys. Photonics. 2020;2
    1. Cnossen J., Hinsdale T., et al. Stallinga S. Localization microscopy at doubled precision with patterned illumination. Nat. Methods. 2020;17:59–63. - PMC - PubMed

LinkOut - more resources