Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Feb 3;16(3):426.
doi: 10.3390/polym16030426.

A Theoretical Investigation of the Polyaddition of an AB2+A2+B4 Monomer Mixture

Sergei V Karpov  1 , Artem Iakunkov  2 , Dmitry A Chernyaev  1 , Vladimir G Kurbatov  1 , Georgiy V Malkov  1 , Elmira R Badamshina  1
Affiliations

A Theoretical Investigation of the Polyaddition of an AB2+A2+B4 Monomer Mixture

Sergei V Karpov et al. Polymers (Basel). .

Abstract

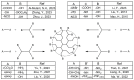
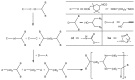
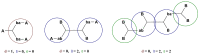
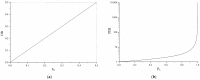
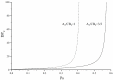
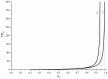
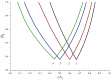
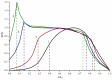
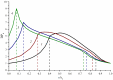
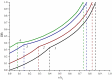
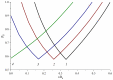
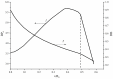
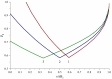
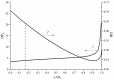
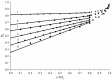
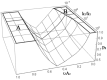
Hyperbranched polymers (HBPs) are widely applied nowadays as functional materials for biomedicine needs, nonlinear optics, organic semiconductors, etc. One of the effective and promising ways to synthesize HBPs is a polyaddition of AB2+A2+B4 monomers that is generated in the A2+CB2, AA'+B3, A2+B'B2, and A2+C2+B3 systems or using other approaches. It is clear that all the foundational features of HBPs that are manufactured by a polyaddition reaction are defined by the component composition of the monomer mixture. For this reason, we have designed a structural kinetic model of AB2+A2+B4 monomer mixture polyaddition which makes it possible to predict the impact of the monomer mixture's composition on the molecular weight characteristics of hyperbranched polymers (number average (DPn) and weight average (DPw) degree of polymerization), as well as the degree of branching (DB) and gel point (pg). The suggested model also considers the possibility of a positive or negative substitution effect during polyaddition. The change in the macromolecule parameters of HBPs formed by polyaddition of AB2+A2+B4 monomers is described as an infinite system of kinetic equations. The solution for the equation system was found using the method of generating functions. The impact of both the component's composition and the substitution effect during the polyaddition of AB2+A2+B4 monomers on structural and molecular weight HBP characteristics was investigated. The suggested model is fairly versatile; it makes it possible to describe every possible case of polyaddition with various monomer combinations, such as A2+AB2, AB2+B4, AB2, or A2+B4. The influence of each monomer type on the main characteristics of hyperbranched polymers that are obtained by the polyaddition of AB2+A2+B4 monomers has been investigated. Based on the results obtained, an empirical formula was proposed to estimate the pg = pA during the polyaddition of an AB2+A2+B4 monomer mixture: pg = pA = (-0.53([B]0/[A]0)1/2 + 0.78)υAB2 + (1/3)1/2([B]0/[A]0)1/2, where (1/3)1/2([B]0/[A]0)1/2 is the Flory equation for the A2+B4 polyaddition, [A]0 and [B]0 are the A and B group concentration from A2 and B4, respectively, and υAB2 is the mole fraction of the AB2 monomer in the mixture. The equation obtained allows us to accurately predict the pg value, with an AB2 monomer content of up to 80%.

Keywords: AB2+A2+B4 monomer mixture; co-polyaddition; degree of branching; gel point; hyperbranched polymers.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflicts of interest.

Figures

Scheme 1
Scheme 1
Synthesis of HBP by polyaddition of the monomer types A2+B3 [23,24,25], A2+B4 [26,27,28], A2+CB2 [29,30,31], and A2+B′B2 [32,33,34].
Scheme 2
Scheme 2
Synthesis of HBP by polyaddition of the monomers of AB2+A2+B4 type [36,37], where ba is the product of interaction between A and B groups, cd is the product of interaction between C and D groups.
Figure 1
Figure 1
Structural units in the AB2+A2+B4 system, where ba/ab is the product of interaction between A and B groups.
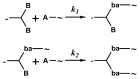
Scheme 3
Scheme 3
Positive and negative substitution effects during the polyaddition of the AB2+A2+B4 monomer mixture, where ba is the product of interaction between A and B groups.
Figure 2
Figure 2
Plot of pg as a function of [A]0/[B]0 for A2+B4 system. Solid line depicts the data obtained through Equation (1), and dots represent the data calculated by the offered approach ([AB2]0 = 0).
Figure 3
Figure 3
Plot of DB as a function of pB (a); plot of PDI as a function of pA (b) in the AB2 monomer-based system ([AB2]0 = 1, [A2]0 = [B4]0 = 0).
Figure 4
Figure 4
Plot of DPw as a function of pB, where the dashed line represents the [AB2]0/[A2]0/[B4]0 = 2/1/1 ([A2]0/[CB2]0 = 1) case, and [AB2]0/[A2]0/[B4]0 = 4/4/1 ([A2]0/[CB2]0 = 3/2) is for the solid line.
Figure 5
Figure 5
Plot of DPw vs. pA when (1) [AB2]0/[A2]0/[B4]0 = 1/0.025/0.097, or (2) [AB2]0/[A2]0/[B4]0 = 1/0.036/0.083. Dashed lines correspond to the pA values of 0.94 and 0.99.
Figure 6
Figure 6
Plot of pg as a function of υA2, where (1) [AB2]0/[B4]0 = 0 (a curve derived from Flory equation); (2) [AB2]0/[B4]0 = 0.5; (3) [AB2]0/[B4]0 = 2; and (4) [AB2]0/[B4]0 = 4.
Figure 7
Figure 7
Plot of specific number of branches per macromolecule (D/N) at pg vs. υA2 when (1) [AB2]0/[B4]0 = 0 (Flory curve); (2) [AB2]0/[B4]0 = 0.5; (3) [AB2]0/[B4]0 = 2; and (4) [AB2]0/[B4]0 = 4. Dashed lines correspond to the points where pg ≤ 1.
Figure 8
Figure 8
Plot of DPn at pg as a function of υA2: (1) [AB2]0/[B4]0 = 0 (Flory curve); (2) [AB2]0/[B4]0 = 0.5; (3) [AB2]0/[B4]0 = 2; and (4) [AB2]0/[B4]0 = 4. Dashed lines correspond to the points where pg ≤ 1.
Figure 9
Figure 9
Plot of DB at pg as a function of υA2: (1) [AB2]0/[B4]0 = 0; (2) [AB2]0/[B4]0 = 0.5; (3) [AB2]0/[B4]0 = 2; and (4) [AB2]0/[B4]0 = 4. Dashed lines correspond to the points where pg ≤ 1.
Figure 10
Figure 10
Graph of pg as a function of υB4, when (1) [AB2]0/[A2]0 = 0 (Flory curve); (2) [AB2]0/[A2]0 = 1/4; (3) [AB2]0/[A2]0 = 2/3; and (4) [AB2]0/[A2]0 = 2.
Figure 11
Figure 11
Plot of DPn—1 and DB—2 vs. υB4, with [AB2]0/[A2]0 = 2/3, and conversion is equal to pg. Dashed line corresponds to the point where pg ≤ 1.
Figure 12
Figure 12
Plot of pg vs. υAB2 at (1)—[A2]0/[B4]0 = 3; (2) [A2]0/[B4]0 = 5; and (3) [A2]0/[B4]0 = 10.
Figure 13
Figure 13
Plot of DPn—1 and DB—2 vs. υAB2 with [A2]0/[B4]0 = 3; conversion is equal pg. Dashed line corresponds to the point where pg ≤ 1.
Figure 14
Figure 14
Plot of pg = pA as a function of υAB2 at [A2]0/[B4]0 ratio equal to (1) 1; (2) 3/2; (3) 2; (4) 3; (5) 5; and (6) 10.
Figure 15
Figure 15
Plot of pg vs. υA2 and k2/k1 if [AB2]0/[B4]0 = 2.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Kaiser T., Frey H. Hyperbranched Polymer Architectures: From Flory’s AB(f-1) Polycondensates to Controlled Structures. Polymer. 2020;211:123113. doi: 10.1016/j.polymer.2020.123113. - DOI
    1. Jeon I.-Y., Noh H.-J., Baek J.-B. Hyperbranched Macromolecules: From Synthesis to Applications. Molecules. 2018;23:657. doi: 10.3390/molecules23030657. - DOI - PMC - PubMed
    1. Caminade A.-M., Yan D., Smith D.K. Dendrimers and Hyperbranched Polymers. Chem. Soc. Rev. 2015;44:3870–3873. doi: 10.1039/C5CS90049B. - DOI - PubMed
    1. Thompson M., Scholz C. Highly Branched Polymers Based on Poly(Amino Acid)s for Biomedical Application. Nanomaterials. 2021;11:1119. doi: 10.3390/nano11051119. - DOI - PMC - PubMed
    1. Saadati A., Hasanzadeh M., Seidi F. Biomedical Application of Hyperbranched Polymers: Recent Advances and Challenges. TrAC Trends Anal. Chem. 2021;142:116308. doi: 10.1016/j.trac.2021.116308. - DOI

LinkOut - more resources