Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Jan 30:12:RP90073.
doi: 10.7554/eLife.90073.

Explicit ion modeling predicts physicochemical interactions for chromatin organization

Xingcheng Lin  1 , Bin Zhang  1
Affiliations

Explicit ion modeling predicts physicochemical interactions for chromatin organization

Xingcheng Lin et al. Elife. .

Abstract

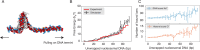
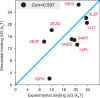
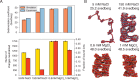
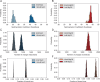
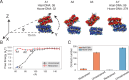
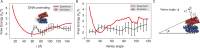
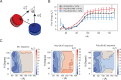
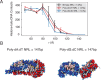
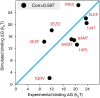
Molecular mechanisms that dictate chromatin organization in vivo are under active investigation, and the extent to which intrinsic interactions contribute to this process remains debatable. A central quantity for evaluating their contribution is the strength of nucleosome-nucleosome binding, which previous experiments have estimated to range from 2 to 14 kBT. We introduce an explicit ion model to dramatically enhance the accuracy of residue-level coarse-grained modeling approaches across a wide range of ionic concentrations. This model allows for de novo predictions of chromatin organization and remains computationally efficient, enabling large-scale conformational sampling for free energy calculations. It reproduces the energetics of protein-DNA binding and unwinding of single nucleosomal DNA, and resolves the differential impact of mono- and divalent ions on chromatin conformations. Moreover, we showed that the model can reconcile various experiments on quantifying nucleosomal interactions, providing an explanation for the large discrepancy between existing estimations. We predict the interaction strength at physiological conditions to be 9 kBT, a value that is nonetheless sensitive to DNA linker length and the presence of linker histones. Our study strongly supports the contribution of physicochemical interactions to the phase behavior of chromatin aggregates and chromatin organization inside the nucleus.

Keywords: 30 nm fiber; chromatin folding; coarse-grained modeling; explicit ions; molecular biophysics; none; structural biology.

PubMed Disclaimer

Conflict of interest statement

XL No competing interests declared, BZ Reviewing editor, eLife

Figures

Figure 1.
Figure 1.. Illustration of the residue-level coarse-grained explicit ion model for chromatin simulations.
The left panel presents a snapshot for the simulation box of a 147 bp nucleosome in a solution of 100 mM NaCl and 0.5 mM MgCl2. The nucleosomal DNA and histone proteins are colored in red and white, respectively. The zoom-in on the right highlights the condensation of ions around the nucleosome, with Na+ in cyan and Mg2+ in yellow. Negative residues of the histone proteins are colored in pink.
Figure 2.
Figure 2.. Explicit ion modeling reproduces the energetics of nucleosomal DNA unwrapping.
(A) Illustration of the umbrella simulation setup using the end-to-end distance between two DNA termini as the collective variable. The same color scheme as in Figure 1 is adopted. Only ions close to the nucleosomes are shown for clarity. (B) Comparison between simulated (black) and experimental (red) free energy profile as a function of the unwrapped DNA base pairs. Error bars were computed as the standard deviation of three independent estimates. (C) The average number of Na+ ions within 10 Å of the nucleosomal DNA (top) and Cl−ions within 10 Å of histone proteins (bottom) are shown as a function of the unwrapped DNA base pairs. Error bars were computed as the standard deviation of three independent estimates.
Figure 2—figure supplement 1.
Figure 2—figure supplement 1.. The explicit ion model predicts the binding affinities of protein-DNA complexes well, related to Figure 1 of the main text.
Experimental and simulated binding free energies are compared for nine protein-DNA complexes (Privalov et al., 2011), with a Pearson correlation coefficient of 0.6. The PDB ID for each complex is indicated in red, and the diagonal line is drawn in blue. The significant correlation between simulated and experimental values supports the accuracy of the model. To further enhance the agreement between the two, it will be necessary to implement specific non-bonded interactions that can resolve differences among amino acids and nucleotides beyond simple electrostatics. Such modifications will be interesting avenues for future research. See text section ‘Binding free energy of protein-DNA complexes’ for simulation details.
Figure 3.
Figure 3.. Explicit ion modeling predicts salt-dependent conformations of a 12-mer nucleosome array.
(A) Top: Comparison of simulated and experimental (Correll et al., 2012) sedimentation coefficients of chromatin at different salt concentrations. Bottom: Number of DNA charges neutralized by bound cations (yellow, left y-axis label) and the fraction of ions bound to DNA (red, right y-axis label) at different salt concentrations. The error bars were estimated from the standard deviation of simulated probability distributions (Figure 3—figure supplement 1). (B) Representative chromatin structures with sedimentation coefficients around the mean values at different salt concentrations.
Figure 3—figure supplement 1.
Figure 3—figure supplement 1.. Probability distributions used to compute means and standard deviations of the quantities presented in Figure 3 of the main text.
(A) Probability distribution of sedimentation coefficients calculated from the simulation with Na+ ions. (B) Probability distribution of sedimentation coefficients calculated from the simulation with Mg2+ ions. (C) Probability distribution of neutralized charges calculated from the simulation with Na+ ions. (D) Probability distribution of neutralized charges calculated from the simulation with Mg2+ ions. (E) Probability distribution of the fraction of bound ions calculated from the simulation with Na+ ions. (F) Probability distribution of the fraction of bound ions calculated from the simulation with Mg2+ ions.
Figure 4.
Figure 4.. Close contacts give rise to strong inter-nucleosomal interactions.
(A) Illustration of the simulation protocol employed to mimic the nucleosome unbinding pathway dictated by the DNA-origami device (Funke et al., 2016). The three configurations, A1, A2, and A3, corresponding to the three cyan dots in part B at distances 62.7, 80.2, and 96.3 Å. For comparison, a tightly bound configuration uncovered in simulations without any restraints of nucleosome movement is shown as A1’. The number of contacts formed by histone tails and DNA (Htail-DNA) and by histone core and DNA (Hcore-DNA) from different nucleosomes is shown for A1 and A1’. (B) Free energy profile as a function of the distance between the geometric centers of the two nucleosomes, computed from unrestrained (black) and DNA-origami-restrained simulations (red). Error bars were computed as the standard deviation of three independent estimates. (C) Average inter-nucleosomal contacts between DNA and histone tail (orange) and core (blue) residues, computed from unrestrained and DNA-origami-restrained simulations. Error bars were computed as the standard deviation of three independent estimates.
Figure 4—figure supplement 1.
Figure 4—figure supplement 1.. Illustration of the restrained two nucleosome simulations setup, related to Figure 4 of the main text.
(A) Schematics of the DNA-origami-based force spectrometer, reproduced from Figure 1 of Funke et al., 2016. (B) Schematics for the spatial restraints imposed on nucleosomes in our simulations to mimic the DNA-origami setup. The vertex angle between two arms of the DNA-origami system is denoted by Φ. The two cartoons on the side illustrate the angle between two nucleosome dyad axes and the angle between two nucleosome planes. To define the coordinate system and other notations, please refer to section ‘Simulations at high salt concentrations’ and the accompanying text.
Figure 4—figure supplement 2.
Figure 4—figure supplement 2.. Explicit ion modeling reproduces the experimental free energy profiles of nucleosome binding.
(A) Comparison between the simulated (black) and experimental (red) free energy profile as a function of the inter-nucleosome distance. Error bars were computed as the standard deviation of three independent estimates. The barrier observed between 60 Å and 80 Å arises from the unwinding of nucleosomal DNA when the two nucleosomes are in close proximity, as highlighted in the orange circle. (B) Comparison between the simulated (black) and experimental (red) free energy profile as a function of the vertex angle. Error bars were computed as the standard deviation of three independent estimates. (C) Illustration of the vertex angle Φ used in panel (B).
Figure 4—figure supplement 3.
Figure 4—figure supplement 3.. Compared with DNA-origami-restrained simulations, the unrestrained simulations produce more histone-DNA contacts across nucleosomes, related to Figure 4 of the main text.
The average number of inter-nucleosome contacts between DNA and histone tails (A) or histone cores (B) is plotted as a function of the distance r. The error bars were estimated as the standard deviation of three equal partitions of the simulations.
Figure 4—figure supplement 4.
Figure 4—figure supplement 4.. The unrestricted simulations favor a smaller angle θ between two nucleosomal planes compared to the DNA-origami-restrained simulations, related to Figure 4 of the main text.
(A) Illustration of the collective variables used in the umbrella-sampling simulation. θ is the angle between two nucleosomal planes, and r is the distance between the geometric centers of two nucleosomes. w1→ and w2→ represent the vectors perpendicular to the nucleosome planes. See text section ‘Simulations at high salt concentrations’ for further definitions of the collective variables. (B) 2D free energy landscape for nucleosome interactions under 35 mM NaCl and 11 mM MgCl2 salt, plotted as a function of r and θ. (C) The average value of θ as a function of the distance r for the unrestricted (red) and the DNA-origami-restrained (black) simulations. The error bars were estimated as the standard deviation of three equal partitions of the simulations.
Figure 5.
Figure 5.. Simulations predict significant inter-nucleosome interactions at physiological conditions.
(A) Illustration of the collective variable, θ, defined as the angle between two nucleosomal planes, and r defined as the distance between the nucleosome geometric centers. w1→ and w2→ represent the axes perpendicular to the nucleosomal planes. (B) The 2D binding free energy profile as a function of θ and r at the physiological salt condition (150 mM NaCl and 2 mM MgCl2) for nucleosomes with the 601 sequence. (C) Dependence of nucleosome binding free energy on nucleosome repeat length (NRL) and linker histone H1.0. Error bars were computed as the standard deviation of three independent estimates. (D) Representative structure showing linker histones (red and blue) mediating inter-nucleosomal contacts.
Figure 5—figure supplement 1.
Figure 5—figure supplement 1.. Dependence of inter-nucleosome interactions on the DNA sequence, related to Figure 5 of the main text.
See text section ‘Simulations at the physiological salt concentration’ for further discussions on simulation details. (A) Illustration of the collective variables used in umbrella-sampling simulations. θ is the angle between two nucleosomal planes, and r is the distance between the geometric centers of two nucleosomes. w1→ and w2→ represent the vectors perpendicular to the nucleosome planes. (B) The free energy profile as a function of the distance r between the geometric centers of two nucleosomes with 601, poly-dA:dT, and poly-dG:dC sequences. Error bars were computed as the standard deviation of three independent estimates. (C) The 2D free energy profiles as a function of θ and r. The simulations used nucleosomes with 601, poly-dA:dT, and poly-dG:dC sequences.
Figure 5—figure supplement 2.
Figure 5—figure supplement 2.. The poly-dA:dT sequence produces a higher number of cross-nucleosome histone-DNA contacts compared to the poly-dG:dC sequence, related to Figure 5 of the main text.
(A) The average number of inter-nucleosome contacts between histone proteins and nucleosomal DNA is plotted as a function of the distance r between the geometric centers of two nucleosomes. The error bars were estimated as the standard deviation of three equal partitions of the simulations. (B) Representative structures from simulations with poly-dA:dT (left) and poly-dG:dC (right) nucleosomes. Noticeable DNA unwrapping can be seen in poly-dA:dT nucleosomes, contributing to the increased cross-nucleosome contacts.
Figure 5—figure supplement 3.
Figure 5—figure supplement 3.. Free energy profiles for the interactions between a pair of nucleosomes at different nucleosome repeat lengths (NRL) and in the presence of the linker histone H1.0, related to Figure 5 of the main text.
See text section ‘Simulations at the physiological salt concentration’ for further discussions on simulation details. (A) Illustration of the collective variables used in the umbrella-sampling simulations. θ is the angle between two nucleosome planes, and r is the distance between the geometric centers of two nucleosomes. w1→ and w2→ represent the vectors perpendicular to the nucleosome planes. (B) 2D free energy profiles as a function of θ and r for the three systems indicated in the titles.
Appendix 1—figure 1.
Appendix 1—figure 1.. A cutoff value of 8.0 Å produces more accurate values for the number of unwrapped DNA base pairs as determined from visual inspection of representative configurations, related to Figure 2 of the main text.
See text section ‘Number of unwrapped DNA base pairs’ for additional discussions. A typical nucleosome structure with most of the outer layer DNA unwrapped was used to examine the impact of different cutoff values. The histone core is colored in gold, with histone tails in white, the wrapped DNA in blue, and the unwrapped DNA in red. The discrepancy among various cutoff values is evident in the highlight regions enclosed by dotted circles. As shown in the zoom-ins in the middle panel, a cutoff of 10 Å results in three additional base pairs of DNA detected as wrapped in I (highlighted in orange square). However, these extra base pairs not detected with a cutoff of 8 Å are visibly detached from histone proteins. Similarly, 9 Å and 10 Å cutoff values result in five extra base pairs of DNA detected as wrapped in II (highlighted in orange squares in the bottom panel).
Author response image 1.
Author response image 1.. Comparison between the radial distribution functions of Na+ (left) and Mg2+ (right) ions around the DNA phosphate groups computed from all-atom (black) and coarse-grained (red) simulations.
Figure reproduced from Figure 4 of [1]. The coarse-grained explicit ion model used in producing the red curves is identical to the one presented in the current manuscript.
Author response image 2.
Author response image 2.. Three-dimensional distribution of sodium ions around the nucleosome determined from all-atom explicit solvent simulations.
Darker blue colors indicate higher sodium density and high density of sodium ions around the DNA is clearly visible. The crystallographically identified acidic patch has been highlighted as spheres on the surface of the histone core and a high level of sodium condensation is observed around these residues. Figure reproduced from [2].
Author response image 3.
Author response image 3.. Time trace of the radius of gyration (Rg) of a nucleosome with the 601-sequence along an unbiased, equilibrium trajectory.
It is evident the Rg fluctuates around the value found in the PDB structure (3.95 nm), supporting the stability of the nucleosome in our simulation.
Author response image 4.
Author response image 4.. The explicit-ion model predicts the binding affinities of protein-DNA complexes well, related to Fig.
1 of the main text. Experimental and simulated binding free energies are compared for nine protein-DNA complexes [cite], with a Pearson Correlation coefficient of 0.6. The PDB ID for each complex is indicated in red, and the diagonal line is drawn in blue. The significant correlation between simulated and experimental values supports the accuracy of the model. To further enhance the agreement between the two, it will be necessary to implement specific non-bonded interactions that can resolve differences among amino acids and nucleotides beyond simple electrostatics. Such modifications will be interesting avenues for future research. See text Section: Binding free energy of protein-DNA complexes for simulation details.
Author response image 5.
Author response image 5.. Revised main text Figure 5, with Figure 5D modified for improved visual clarity.
Author response image 6.
Author response image 6.. Explicit ion modeling reproduces the experimental free energy profiles of nucleosome binding.
(A) Comparison between the simulated (black) and experimental (red) free energy profile as a function of the inter-nucleosome distance. Error bars were computed as the standard deviation of three independent estimates. The barrier observed between 60Å and 80Å arises from the unwinding of nucleosomal DNA when the two nucleosomes are in close proximity, as highlighted in the orange circle. (B) Comparison between the simulated (black) and experimental (red) free energy profile as a function of the vertex angle. Error bars were computed as the standard deviation of three independent estimates. (C) Illustration of the vertex angle Φ used in panel (B).
See this image and copyright information in PMC

Update of

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Allahverdi A, Chen Q, Korolev N, Nordenskiöld L. Chromatin compaction under mixed salt conditions: opposite effects of sodium and potassium ions on nucleosome array folding. Scientific Reports. 2015;5:8512. doi: 10.1038/srep08512. - DOI - PMC - PubMed
    1. Bajpai G, Amiad Pavlov D, Lorber D, Volk T, Safran S. Mesoscale phase separation of chromatin in the nucleus. eLife. 2021;10:e63976. doi: 10.7554/eLife.63976. - DOI - PMC - PubMed
    1. Bancaud A, Wagner G, Conde E Silva N, Lavelle C, Wong H, Mozziconacci J, Barbi M, Sivolob A, Le Cam E, Mouawad L, Viovy J-L, Victor J-M, Prunell A. Nucleosome chiral transition under positive torsional stress in single chromatin fibers. Molecular Cell. 2007;27:135–147. doi: 10.1016/j.molcel.2007.05.037. - DOI - PubMed
    1. Bascom G, Schlick T. Nuclear Architecture and Dynamics. Elsevier; 2018. - DOI
    1. Bennink ML, Leuba SH, Leno GH, Zlatanova J, de Grooth BG, Greve J. Unfolding individual nucleosomes by stretching single chromatin fibers with optical tweezers. Nature Structural Biology. 2001;8:606–610. doi: 10.1038/89646. - DOI - PubMed