Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Jan 25;14(1):2175.
doi: 10.1038/s41598-023-51121-0.

Qualitative analysis and chaotic behavior of respiratory syncytial virus infection in human with fractional operator

Saba Jamil  1 , Abdul Bariq  2 , Muhammad Farman  1   3   4 , Kottakkaran Sooppy Nisar  5 , Ali Akgül  3   4   6 , Muhammad Umer Saleem  7
Affiliations

Qualitative analysis and chaotic behavior of respiratory syncytial virus infection in human with fractional operator

Saba Jamil et al. Sci Rep. .

Erratum in

Abstract

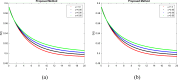
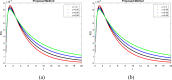
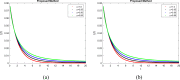
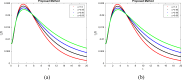
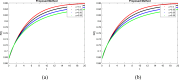
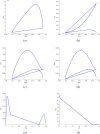
Respiratory syncytial virus (RSV) is the cause of lung infection, nose, throat, and breathing issues in a population of constant humans with super-spreading infected dynamics transmission in society. This research emphasizes on examining a sustainable fractional derivative-based approach to the dynamics of this infectious disease. We proposed a fractional order to establish a set of fractional differential equations (FDEs) for the time-fractional order RSV model. The equilibrium analysis confirmed the existence and uniqueness of our proposed model solution. Both sensitivity and qualitative analysis were employed to study the fractional order. We explored the Ulam-Hyres stability of the model through functional analysis theory. To study the influence of the fractional operator and illustrate the societal implications of RSV, we employed a two-step Lagrange polynomial represented in the generalized form of the Power-Law kernel. Also, the fractional order RSV model is demonstrated with chaotic behaviors which shows the trajectory path in a stable region of the compartments. Such a study will aid in the understanding of RSV behavior and the development of prevention strategies for those who are affected. Our numerical simulations show that fractional order dynamic modeling is an excellent and suitable mathematical modeling technique for creating and researching infectious disease models.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Figure 1
Figure 1
Simulation of S(t). (a) p=0.001, (b) p=0.0004 under the Caputo model.
Figure 2
Figure 2
Simulation of E(t). (a) p=0.001, (b) p=0.0004 under the Caputo model.
Figure 3
Figure 3
Simulation of Ir(t). (a) p=0.001, (b) p=0.0004 under the Caputo model.
Figure 4
Figure 4
Simulation of Is(t). (a) p=0.001, (b) p=0.0004 under the Caputo model.
Figure 5
Figure 5
Simulation of R(t). (a) p=0.001, (b) p=0.0004 under the Caputo model.
Figure 6
Figure 6
Simulation of chaotic behavior of compartments. (a) Behavior of S(t) and E(t). (b) Behavior of S(t) and Ir(t). (c) Behavior of S(t) and Is(t). (d) Behavior of S(t) and R(t). (e) Behavior of Ir(t) and Is(t). (f) Behavior of Ir(t) and R(t).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Arenas AJ, González G, Jódar L. Existence of periodic solutions in a model of respiratory syncytial virus RSV. J. Math. Anal. Appl. 2008;344(2):969–980. doi: 10.1016/j.jmaa.2008.03.049. - DOI
    1. Weber A, Weber M, Milligan P. Modeling epidemics caused by respiratory syncytial virus (RSV) Math. Biosci. 2001;172(2):95–113. doi: 10.1016/S0025-5564(01)00066-9. - DOI - PubMed
    1. Glezen WP, Taber LH, Frank AL, Kasel JA. Risk of primary infection and reinfection with respiratory syncytial virus. Am. J. Dis. Child. 1986;140(6):543–546. - PubMed
    1. Rao F, Mandal PS, Kang Y. Complicated endemics of an SIRS model with a generalized incidence under preventive vaccination and treatment controls. Appl. Math. Model. 2019;67:38–61. doi: 10.1016/j.apm.2018.10.016. - DOI
    1. Lin J, Xu R, Tian X. Global dynamics of an age-structured cholera model with both human-to-human and environment-to-human transmissions and saturation incidence. Appl. Math. Model. 2018;63:688–708. doi: 10.1016/j.apm.2018.07.013. - DOI