Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
[Preprint]. 2024 Jan 10:2024.01.09.574885.
doi: 10.1101/2024.01.09.574885.

Growth-induced collective bending and kinetic trapping of cytoskeletal filaments

Deb Sankar Banerjee  1   2 , Simon L Freedman  3 , Michael P Murrell  4   5   6 , Shiladitya Banerjee  1
Affiliations

Growth-induced collective bending and kinetic trapping of cytoskeletal filaments

Deb Sankar Banerjee et al. bioRxiv. .

Update in

Abstract

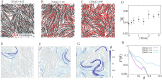
Growth and turnover of actin filaments play a crucial role in the construction and maintenance of actin networks within cells. Actin filament growth occurs within limited space and finite subunit resources in the actin cortex. To understand how filament growth shapes the emergent architecture of actin networks, we developed a minimal agent-based model coupling filament mechanics and growth in a limiting subunit pool. We find that rapid filament growth induces kinetic trapping of highly bent actin filaments. Such collective bending patterns are long-lived, organized around nematic defects, and arises from competition between filament polymerization and bending elasticity. The stability of nematic defects and the extent of kinetic trapping are amplified by an increase in the abundance of the actin pool and by crosslinking the network. These findings suggest that kinetic trapping is a robust consequence of growth in crowded environments, providing a route to program shape memory in actin networks.

Keywords: actin network assembly; agent-based modeling; filament growth; kinetic trapping; topological defects.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.. Filament length control in a limiting monomer pool.
(A) Schematic showing the model for actin filament growth within a limiting pool of monomers (B) Fluctuation in filament length over one hour for three different monomer pool sizes: 1μm (top), 10μm (middle), and 100μm (bottom). (C) Filament length distribution at different monomer pool sizes. (D) Mean filament length as a function of number of filaments (NF). (E) Configurations of a collection of growing filaments at (left to right) t=0.35s, 3.5s, 17.5s, 35s, and 70s. Parameters values used here are k+=11.4∕μMs, k−=1∕s and NF=10 for different pool sizes in B and C. For panel D, [actin]=10μM and for panel E, [actin]=15μM, and NF=68.
Fig. 2.
Fig. 2.. Collective bending pattern and kinetic trapping of filaments.
(A) Configurations of actin filament assemblies for different nucleator densities (i.e., different filament lengths). (B) Quantification of filament bending by the compressive strain θ. (C) Time evolution of average compressive strain per filament, 〈θ(t)〉, for different filament lengths. (D) Steady-state value of the ensemble-averaged compressive strain per filament, for different filament lengths. (E) Dynamics of the average bending energy per filament, for different filament lengths. (F) Average bending energy for different nucleator numbers for varying bending rigidity. (G) Time-lapse of filament configurations in growing networks, with filaments color coded by their compressive strains. Over time we observe the emergence of correlated bending due to kinetic trapping of high curvature filaments (dashed circle). The actin density is 15μM for all results shown here. For panel G, NF=64(L=15μm).
Fig. 3.
Fig. 3.. Nematic alignment and topological defects in filament assembly.
(A) A representative configuration of a filament assembly, showing the distribution of half-integer defects. +1/2 defects are shown by solid yellow circles and −1/2 defects are shown in purple. (B) Spatial profile of local nematic order S for the filamentous network shown in panel (A). The black dots represent the position of half-integer defects. The yellow regions of ~ 0 nematic order around the defects indicate the defect core size. (C) Defect density as a function of the number of filaments. (D) Spatially averaged nematic order 〈S〉, as a function of the number of filaments. (E) Time-lapse sequences showing the evolution of actin filament configurations during growth at an actin concentration of 15μM. The shaded yellow region highlights an example of structural relaxation, where filament bending gradually relaxes over time, resulting in the disappearance of the defect. (F) Time-lapse sequences illustrating the configurations of actin filaments at a high actin concentration of 30μM. In this scenario, topological defects are long-lived as filament bends are unable to relax due to high crowding. In simulations for panels A-E, we chose [actin]=15μM. For panels A-B, NF=64(L=15μm). For C and D, NF=97(L=10μm) and the results are averaged over 8 independent simulations.
Fig. 4.
Fig. 4.. Effects of actin density on filament mechanics.
(A) Filament configurations for different actin densities. (B) Average filament bending at the same filament length (10μm) with increasing actin density. (C) Average bending energy at the same filament length (10μm) with increasing actin density. Here L=10μm for all actin densities (i.e., different NF values) and the results are averaged over 8 independent simulations.
Fig. 5.
Fig. 5.. Crosslinking enhances filament bending.
(A-C) Filament configurations for different crosslinker densities. The crosslinker is plotted in red. (D) Average filament bending with increasing crosslinker density. (E-G) Filament configurations coloured by filament bending for different crosslinker densities (same as A-C panels). (H) Probability distribution P(θ) of filament bending (θ) for different crosslinker densities. Here [actin]=15μM and NF=97(L=10μm) and the results are averaged over 8 independent simulations.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Pollard Thomas D and Borisy Gary G. Cellular motility driven by assembly and disassembly of actin filaments. Cell, 112(4):453–465, 2003. - PubMed
    1. Banerjee Shiladitya, Gardel Margaret L, and Schwarz Ulrich S. The actin cytoskeleton as an active adaptive material. Annual review of condensed matter physics, 11:421–439, 2020. - PMC - PubMed
    1. Svitkina Tatyana. The actin cytoskeleton and actin-based motility. Cold Spring Harbor perspectives in biology, 10(1):a018267, 2018. - PMC - PubMed
    1. Blanchoin Laurent, Boujemaa-Paterski Rajaa, Sykes Cécile, and Plastino Julie. Actin dynamics, architecture, and mechanics in cell motility. Physiological reviews, 94(1):235–263, 2014. - PubMed
    1. Mallavarapu Aneil and Mitchison Tim. Regulated actin cytoskeleton assembly at filopodium tips controls their extension and retraction. The Journal of cell biology, 146(5):1097–1106, 1999. - PMC - PubMed

Publication types