Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2023 Oct 19;15(10):2119.
doi: 10.3390/v15102119.

Mathematical Models of HIV-1 Dynamics, Transcription, and Latency

Iván D'Orso  1 , Christian V Forst  2
Affiliations
Review

Mathematical Models of HIV-1 Dynamics, Transcription, and Latency

Iván D'Orso et al. Viruses. .

Abstract

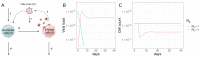
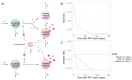
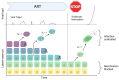
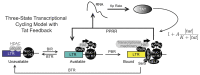
HIV-1 latency is a major barrier to curing infections with antiretroviral therapy and, consequently, to eliminating the disease globally. The establishment, maintenance, and potential clearance of latent infection are complex dynamic processes and can be best described with the help of mathematical models followed by experimental validation. Here, we review the use of viral dynamics models for HIV-1, with a focus on applications to the latent reservoir. Such models have been used to explain the multi-phasic decay of viral load during antiretroviral therapy, the early seeding of the latent reservoir during acute infection and the limited inflow during treatment, the dynamics of viral blips, and the phenomenon of post-treatment control. Finally, we discuss that mathematical models have been used to predict the efficacy of potential HIV-1 cure strategies, such as latency-reversing agents, early treatment initiation, or gene therapies, and to provide guidance for designing trials of these novel interventions.

Keywords: HIV-1; latency; mathematical modeling; reactivation; stochastic fluctuations; transcription.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
The basic viral dynamics model. (A) Cell population processes that are simulated in the mathematical model (Equation (1)). (B,C) Example trajectory of viral load (V) and uninfected target cells (CD4 T cells, T) when R0>1 (red) and R0<1 (blue). Graphs were generated by numerically integrating Equation (1) with parameters λ=100 cells/µL, β=7×10−5 or 0/day/(virus/mL), k=150 virus/cell, dT=0.05/day, dI=0.7/day, c=1.7/day using JSim v2.21 with standard integration parameters [32]. (Figure adapted from Hill [18] and created by part (A) with BioRender.com).
Figure 2
Figure 2
Schematic of a viral dynamics model involving multiple populations of infected cells. (A) A flow diagram between two populations of uninfected cells (T, T2), virus infected cells (I, I2), a latently infected cell population (L) and free HIV-1 (V) according to the ODE shown in Equation (4). Red X’es indicate the complete interruption of viral infection during fully effective therapy. (B) The decay of the viral load in multiple stages is shown. (C) The decay of distinct host-cell populations, as predicted by the model, are depicted. Time-series were integrated using JSim v2.21 with standard integration parameters [32]. (Figure adapted from Hill [18] and created by part (A) with BioRender.com).
Figure 3
Figure 3
Schematic of latent reservoir dynamics. The latent reservoir involves long-lived resting memory CD4 cells, with potentially integrated HIV-1 provirus. At subcritical viral replication rate (R0<1), the persistence of virus represents the maintenance of the latent reservoir. Infected host cells within this reservoir may occasionally die (marked by skull and bones), proliferate, or reactivate. A large proliferation rate leads to a decrease in viral diversity within the latent reservoir. New infections (bursts) are either completely blocked (Reactivation blocked) or may occasionally occur by stochastic processes. But continuous chains of replication are inhibited in the R0<1 regime (Infection controlled). After treatment interruption (R0>1), reactivated cells can produce virus that infects other host cells yielding to exponential growth in viral load (see Section 4, in particular Figure 4C). (Figure adapted from Hill [18] and created with BioRender.com).
Figure 4
Figure 4
Mathematical model of the host and viral phases of the HIV-1 transcriptional program [121]. (A) Simplified model of the host and viral phases of the HIV-1 transcriptional program. (B) Experimental data and fitted stochastic computer simulation of a host cell infected by HIV-1 in the host phase without feedback by Tat. (C) Experimental data and fitted stochastic computer simulation of a host cell infected by HIV-1 in the viral phase with feedback by Tat.
Figure 5
Figure 5
Positive feedback on the RNAPII pause release rate (PPRR) activation does not influence bimodality of the mRNA and protein distributions in the three-state transcriptional cycling model [109]. Updated three-state promoter system with HIV-1 nucleosome remodeling, RelA recruitment, and Tat-mediated transcript elongation, which is amplified via positive feedback. Positive feedback is modeled as a saturating function with an amplitude, A, and half-max, K.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Chun T.W., Carruth L., Finzi D., Shen X., DiGiuseppe J.A., Taylor H., Hermankova M., Chadwick K., Margolick J., Quinn T.C., et al. Quantification of latent tissue reservoirs and total body viral load in HIV-1 infection. Nature. 1997;387:183–188. doi: 10.1038/387183a0. - DOI - PubMed
    1. Finzi D., Hermankova M., Pierson T., Carruth L.M., Buck C., Chaisson R.E., Quinn T.C., Chadwick K., Margolick J., Brookmeyer R., et al. Identification of a reservoir for HIV-1 in patients on highly active antiretroviral therapy. Science. 1997;278:1295–1300. doi: 10.1126/science.278.5341.1295. - DOI - PubMed
    1. Finzi D., Blankson J., Siliciano J.D., Margolick J.B., Chadwick K., Pierson T., Smith K., Lisziewicz J., Lori F., Flexner C., et al. Latent infection of CD4+ T cells provides a mechanism for lifelong persistence of HIV-1, even in patients on effective combination therapy. Nat. Med. 1999;5:512–517. doi: 10.1038/8394. - DOI - PubMed
    1. Kumar A., Abbas W., Herbein G. HIV-1 latency in monocytes/macrophages. Viruses. 2014;6:1837–1860. doi: 10.3390/v6041837. - DOI - PMC - PubMed
    1. Mitchell B.I., Laws E.I., Ndhlovu L.C. Impact of myeloid reservoirs in HIV cure trials. Curr. HIV/AIDS Rep. 2019;16:129–140. doi: 10.1007/s11904-019-00438-5. - DOI - PMC - PubMed

Publication types