Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jul 17;13(1):11541.
doi: 10.1038/s41598-023-38558-z.

Application of quantum machine learning using quantum kernel algorithms on multiclass neuron M-type classification

Xavier Vasques  1   2   3 , Hanhee Paik  4 , Laura Cif  5
Affiliations

Application of quantum machine learning using quantum kernel algorithms on multiclass neuron M-type classification

Xavier Vasques et al. Sci Rep. .

Abstract

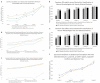
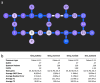
The functional characterization of different neuronal types has been a longstanding and crucial challenge. With the advent of physical quantum computers, it has become possible to apply quantum machine learning algorithms to translate theoretical research into practical solutions. Previous studies have shown the advantages of quantum algorithms on artificially generated datasets, and initial experiments with small binary classification problems have yielded comparable outcomes to classical algorithms. However, it is essential to investigate the potential quantum advantage using real-world data. To the best of our knowledge, this study is the first to propose the utilization of quantum systems to classify neuron morphologies, thereby enhancing our understanding of the performance of automatic multiclass neuron classification using quantum kernel methods. We examined the influence of feature engineering on classification accuracy and found that quantum kernel methods achieved similar performance to classical methods, with certain advantages observed in various configurations.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Figure 1
Figure 1
Neuronal morphologies– from the NeuroMorpho-rat dataset. Principal neurons are presented, such as (a) a pyramidal cell (layer 4, C010398B-P2) from the rat somatosensory neocortex; (b) a ganglion cell (LY8-RGC1) from the retina; (c) a granule cell (03D23APV-1) from the hippocampus; (d) a medium spiny cell (1-1-DE) from the nucleus accumbens; (e) a parachromatin cell (D20c) from the adrenal medulla; and (f) a Purkinje cell (alxP) from the cerebellum. Interneurons from the rat somatosensory neocortex are presented, such as (g) a basket cell (layer 2–3, C010398B-I4); (h) a bitufted cell (layer 4, C020600C1); (i) a chandelier cell (layer 2–3, C231001B2); (j) a double bouquet (layer 2–3, C060400B2); (k) a Martinotti cell (layer 2–3, C050398B-IA); and (l) a nitrergic cell (layer 5–6, RatS1-1-1). In addition, we demonstrated two types of glial cells: (m) a microglia cell (farsight624) from the frontal neocortex and (n) astrocyte cells (A1-CA1-L-C63x1zACR1) from the hippocampus. (o) Feature’s importance using XGBoost, decision tree, and random forest applied to the entire dataset (sample 5). (p) Definition of the 43 morphological features extracted for each neuron.They were extracted using the L-Measure tool, providing quantitative morphological measurement from neuronal reconstruction (http://cng.gmu.edu:8080/Lm/help/index.htm). (q) Dataset with the number of neuron morphologies for multiclass classification. From the 27,881 extracted neurons, 22,691 neurons (sample 5) remained after the application of Mahalanobis distance transformation and the suppression of all neurons with a soma surface equal to 0.
Figure 2
Figure 2
Cross-validation scores of the different algotihms (a) Cross-validation scores of q_kernel_training run on five qubits with the combination of the quantile-Gaussian technique for data rescaling and a decision tree for feature selection; classical SVM with RBF kernel using the combination of Yeo–Johnson for data rescaling and a random forest for feature selection; and q_kernel_zz run on five qubits using the combination of the quantile-uniform technique and a decision tree, which were applied to the samples described in Fig. 1. The results were obtained by running the algorithms with five selected features. (b) Five-fold cross-validation scores obtained with the combination of the quantile-uniform technique for feature rescaling and a decision tree for feature selection to compare the performance of q_kernel_zz (five qubits) and classical SVMs with RBF, linear, polynomial, and sigmoid using five selected features on all of the samples described in Fig. 1 (sample 1 = 260 neurons, sample 2 = 626, sample 3 = 1143, sample 4 = 2080, sample 5 = 22,691). (c) Five-fold cross-validation scores obtained with a combination of the quantile-Gaussian technique for feature rescaling and a decision tree for feature selection to compare the performance of q_kernel_training (five qubits) and classical SVMs with RBF, linear, polynomial, and sigmoid kernels using five selected features on all samples. (d) Five-fold cross-validation scores obtained from the combination of the quantile-uniform and Yeo–Johnson techniques for feature rescaling and a decision tree for feature selection, comparing the performance of q_kernel_zz (20 qubits) and classical SVMs with RBF to classify neuron morphologies using 20 selected features on all of the samples described in Fig. 1 (sample 1 = 260 neurons, sample 2 = 626, sample 3 = 1143, sample 4 = 2080, sample 5 = 22,691). (e) Five-fold cross-validation scores obtained from a combination of the quantile-uniform and Yeo–Johnson techniques for feature rescaling and a decision tree for feature selection to compare the performance of q_kernel_zz (10 qubits) and classical SVMs with RBF to classify neuron morphologies using 10 selected features on all samples. (f) Cross-validation scores of q_kernel_zz run with five qubits with a combination of the quantile-uniform technique for data rescaling and a decision tree for feature selection on both quantum hardware and statevector simulation applied to the different samples described in Fig. 1.
Figure 3
Figure 3
Quantum Systems (a) Qubit connectivity of the four 27-qubit superconducting quantum computers. Lighter colors mean a higher T2 time for qubits and lower fidelity for coupling. (b) Characteristics of the four quantum systems.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Feynman, R. Simulating physics with computers. In International Journal of Theo- retical Physics (1981).
    1. Shor, P. Algorithms for quantum computation: Discrete logarithms and factoring. In Proc. 35th annual symposium on findations of computer scienceIeee, 124–134 (1994).
    1. Grover, L. K. A fast quantum mechanical algorithm for database search. In Proc. of the twenty-eighth annual ACM symposium on Theory of computing 212–219 (1996).
    1. Havlíček V, et al. Supervised learning with quantum-enhanced feature spaces. Nature. 2019;567:209–212. doi: 10.1038/s41586-019-0980-2. - DOI - PubMed
    1. Coles PJ. Seeking quantum advantage for neural networks. Nat. Comput. Sci. 2021;1:389–390. doi: 10.1038/s43588-021-00088-x. - DOI - PubMed