Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jul 7:568:111497.
doi: 10.1016/j.jtbi.2023.111497. Epub 2023 Apr 21.

Statistical inference of the rates of cell proliferation and phenotypic switching in cancer

Einar Bjarki Gunnarsson  1 , Jasmine Foo  2 , Kevin Leder  3
Affiliations

Statistical inference of the rates of cell proliferation and phenotypic switching in cancer

Einar Bjarki Gunnarsson et al. J Theor Biol. .

Abstract

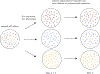
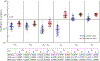
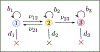
Recent evidence suggests that nongenetic (epigenetic) mechanisms play an important role at all stages of cancer evolution. In many cancers, these mechanisms have been observed to induce dynamic switching between two or more cell states, which commonly show differential responses to drug treatments. To understand how these cancers evolve over time, and how they respond to treatment, we need to understand the state-dependent rates of cell proliferation and phenotypic switching. In this work, we propose a rigorous statistical framework for estimating these parameters, using data from commonly performed cell line experiments, where phenotypes are sorted and expanded in culture. The framework explicitly models the stochastic dynamics of cell division, cell death and phenotypic switching, and it provides likelihood-based confidence intervals for the model parameters. The input data can be either the fraction of cells or the number of cells in each state at one or more time points. Through a combination of theoretical analysis and numerical simulations, we show that when cell fraction data is used, the rates of switching may be the only parameters that can be estimated accurately. On the other hand, using cell number data enables accurate estimation of the net division rate for each phenotype, and it can even enable estimation of the state-dependent rates of cell division and cell death. We conclude by applying our framework to a publicly available dataset.

Keywords: Cancer evolution; Epigenetics; Mathematical modeling; Maximum likelihood estimation; Parameter identifiability; Phenotypic switching.

PubMed Disclaimer

Conflict of interest statement

Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Figure 1:
Figure 1:
The dynamics of phenotypic switching are commonly interrogated by sorting live cells into isolated phenotypic subpopulations and expanding these subpopulations in culture [21, 17, 19, 20, 23, 24, 14]. By tracking the evolution of phenotypic proportions over time and applying mathematical models of phenotypic switching, it becomes possible to estimate the quantitative parameters of the process [21, 26, 27, 28, 29, 22, 12, 30].
Figure 2:
Figure 2:
The multitype branching process model captures a variety of switching dynamics previously observed in the literature. (a) A two-type model captures e.g. the dynamics between HER2+ and HER2− cell states in Brx-82 and Brx-142 breast cancer cells [23]. (b) A three-type model captures e.g. the dynamics between stem-like, basal and luminal cell states in SUM149 and SUM159 breast cancer cells [21]. (c) A four-type model captures e.g. the dynamics between CD24Low/ALDHHigh, CD24Low/ALDHLow, CD24High/ALDHHigh and CD24Hich/ALDHLow cell states in GBC02, SCC029B and SCC070 oral cancer cells [32].
Figure 3:
Figure 3:
Assessment of estimation error across a wide range of biologically realistic parameter regimes. We first generated 100 different parameter regimes, then generated 100 artificial datasets for each regime, and finally computed parameter estimates for each dataset. To generate the parameter regimes, we sampled birth and death rates uniformly between 0 and 1, and sampled switching rates log-uniformly between 10−1 and 10−3 (Appendix H). For each parameter and each parameter regime, we used the 100 estimates to compute the coefficient of variation (CV) for the estimates, which measures the error in the estimation. Each dot in the figure represents the CV for a single parameter under a single regime, with the blue dots (resp. red dots) representing estimates from cell number data (resp. cell fraction data). Collectively, the dots enable comparison of estimation error between different model parameters and between cell number and cell fraction data. The horizontal bars represent the 10th percentile, median and 90th percentile of the CVs, bottom to top.
Figure 4:
Figure 4:
Two ways of improving the estimation accuracy for the birth rates b when cell number data is used. In (a), we show how the estimation accuracy for the birth rate b1 improves as the number of experimental replicates is increased. In (b), we compare the estimation accuracy for the birth rate b1 and the net birth rate λ1 depending on whether data on the number of dead cells at each time point is included in the estimation or not.
Figure 5:
Figure 5:
Augmentation of the mathematical model for when data is available on the number of dead cells at each time point. In that case, in stead of cells being lost from the model upon dying (left panel), they transition into a new state (right panel).
Figure 6:
Figure 6:
Comparison of estimation error depending on whether our framework is applied to endpoint data or sequential data. The blue dots show the estimation error when endpoint data is used, i.e. when experiments from different time points are independent, and the red dots show the error when sequential data is used, i.e. when data is collected at multiple time points in the same experiment. Panel (a) shows the comparison for cell number data and panel (b) for cell fraction data. Even though our framework is derived for endpoint data, it provides reasonable estimation accuracy for sequential data.
Figure 7:
Figure 7:
Visual comparison of point estimates and 95% confidence intervals for the statistical model fj,ℓ ∼p(j)(tℓ)+𝓝0,ω2I (Model Ia) and the same model with λ2−λ1=0 (Model IIa) applied to publicly available cell fraction data from Yang et al. [17].
Figure 8:
Figure 8:
To demonstrate that our estimation framework is applicable to reducible switching models, we consider a three-type model with a reversible transition between type-1 and type-2, and an irreversible transition from type-2 to type-3. This model is applicable e.g. to epigenetic gene silencing under the recruitment of chromatin regulators [36] and to epigenetically-driven drug resistance in cancer [25].
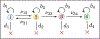
Figure 9:
Figure 9:
An example of a four-type switching model where the likelihood function (24) for cell fraction data from the main text must be modified to avoid degeneracy issues. This model structure can e.g. arise in the context of epigenetically-driven drug resistance in cancer, where drug-sensitive (type-0) cells can acquire transient resistance (type-1), which then evolves gradually to stable resistance (type-4) in two steps [25].
Figure 10:
Figure 10:
Graphical depiction of the output of our estimation framework. We first generated artificial cell-number and cell-fraction data by simulating the branching process model of Section 3.1 for b1=0.6, d1=0.3, b2=1.0, d2=0.5, ν12=0.02, ν21=0.04 and N1=N2=1,000. Using this data, we computed maximum likelihood estimates and likelihood-based 95% confidence intervals (CIs) for the model parameters. For each parameter, the shaded region indicates the CI, the vertical bar inside the interval indicates the MLE estimate, and the arrow points to the true value of the parameter.
Figure 11:
Figure 11:
Comparison of estimation error for different experimental designs when the number of data points is doubled. We generated 10 parameter regimes and 100 datasets for each regime. The blue dots represent estimation from datasets with L=6 time points and R=3 replicates. The red dots represent estimation from L=6 time points and R=6 replicates. The green and grey dots represent estimation from L=12 time points and R=3 replicates, where the extra time points are added in between and after the previous time points, respectively. Panel (a) shows estimation from cell number data and panel (b) shows estimation from cell fraction data.
See this image and copyright information in PMC

Update of

Similar articles

See all similar articles

Cited by

References

    1. Brock Amy, Chang Hannah, and Huang Sui. Non-genetic heterogeneity - a mutation-independent driving force for the somatic evolution of tumours. Nature Reviews Genetics, 10(5):336, 2009. - PubMed
    1. Peter A Jones and Stephen B Baylin. The epigenomics of cancer. Cell, 128(4):683–692, 2007. - PMC - PubMed
    1. Brown Robert, Curry Edward, Magnani Luca, Charlotte S Wilhelm-Benartzi, and Jane Borley. Poised epigenetic states and acquired drug resistance in cancer. Nature Reviews Cancer, 14(11):747, 2014. - PubMed
    1. Flavahan William A, Gaskell Elizabeth, and Bernstein Bradley E. Epigenetic plasticity and the hallmarks of cancer. Science, 357(6348):eaal2380, 2017. - PMC - PubMed
    1. Salgia Ravi and Kulkarni Prakash. The genetic/non-genetic duality of drug ‘resistance’in cancer. Trends in cancer, 4(2):110–118, 2018. - PMC - PubMed

Publication types

LinkOut - more resources